---

V-Optimal Histograms

---

• What are V-Optimal Histograms ?
  • Let X = x₁, x₂, x₃, ... x_N be a finite data sequence.

  • Let B be the number of buckets (the value of B is given, i.e., it's a parameter of the problem formulation)

  • The histogram H_B is a histogram that uses at most B buckets.

  • The (typical) histogram representation collapses a sequence values x_s, x_s+1, x_s+2, ... x_e into a single point h_r of the histogram.
    • The range from x_s to x_s forms the bucket
    • The point x_s is the start point of the bucket
    • The point x_e is the end point of the bucket

    • The value h_r is used as an estimate for all the values x_s, x_s+1, x_s+2, ... x_e !!!

      In other words, after you construct the histogram, when someone asks you:

      • What is the value x_s+1 ?

      Your answer must be based on the histogram and therefore, you will answer:

      • the value is h_r

    • You will incur an error of h_r - x_s+1 to the inquiry of x_s+1.

    • The expression h_r - x_s+1 canbe positive or negative; for practical purposes, we prefer expression for errors that is always positive (because errors are penalty values

      It is common to use |h_r - x_s+1| (absolute value) or (h_r - x_s+1)² as expression for the error.

      The expression (h_r - x_s+1)² is prefered because it is differentiable .

  • The squared error for the values in bucket b_r is:
    SqError(b_r) = ∑_k=sr..er (h_r - x_k)²

    The following figure shows what this error represents:

    • Notice that SqError(b_r) will change when a different value for h_r is used !!!

    • One of the problems that we must solve is:
      What value should h_r be so that SqError(b_r) is minimized

  • Let E_X(H_B) be the total error between the actual data sequence X and the histogram H_B values:
    SqError(histogram) = ∑_r=1..B ( ∑_k=sr..er (h_r - x_k)² )
    • Notice that SqError(histogram) will change when we divide the domain up into different bucket ranges (even when we use the same number of bucket B)

    • Another problem that we must solve is:
      What are the ranges of the B buckets so that SqError(histogram) is minimized

  • The V-Optimal histogram is the histogram of B buckets Histogram((s_r, e_r, h_r), r = 1, 2, .., B) that minimizes the histogram error SqError(histogram)

  ---

  ---

• Finding the histogram with the minimum error - Part 1 (value for a bucket)
  • It may seem almost impossible to find the histogram that minimizes the Square Error at first glance, but researchers have come up with some very fast algorithm to find the V-optimal histogram.

  • Notice that there are 2 subproblems involved in finding the V-optimal histogram:
    1. First we have to divide the domain into the "best" ranges, i.e., find the buckets (ranges) of the optimal histogram

    2. Then, for each bucket b_r, determine the value h_r that minimizes the error within that bucket.

  • We will first deal with the second problem (which is the easiest).

    So, let us now assume that the optimum bucket division has been found already (so the bucket ranges are fixed)...

  • The expression for the error of the histogram
    SqError(histogram) = ∑_r=1..B ( ∑_k=sr..er (h_r - x_k)² )

    is in fact the following sum:

    SqError(histogram) = ∑_k=s1..e1 (h₁ - x_k)² + ∑_k=s2..e2 (h₂ - x_k)² + ... + ∑_k=sB..eB (h_B - x_k)²

  • If the bucket boundaries do not change, that means that s₁, e₁, s₂, e₂, ... s_B, e_B are constant

  • Then the whole sum
    SqError(histogram) = ∑_k=s1..e1 (h₁ - x_k)² + ∑_k=s2..e2 (h₂ - x_k)² + ... + ∑_k=sB..eB (h_B - x_k)²

    is minimized if individual sums are minimized.

    (This sounds subtle, but if just think how much more complex the minimalization process would be if the boundary was NOT fixed. When the boundaries are not fixed, some values of x_k are subtracted from different h_r's and we could not make the above statement....)

  • Consider one of the sums in SqError(histogram) which is the error made in some bucket b_r:
    S_r = ∑_k=sr..er (h_r - x_k)²

    It may be clearer if you write the sum out:

    S_r = (h_r - x_sr)² + (h_r - x_sr+1)² + (h_r - x_sr+2)² + .... + (h_r - x_er)²

  • Each of the x_... is constant value, so S_r depends only on h_r:
    S_r = (h_r - c₁)² + (h_r - c₂)² + (h_r - c₃)² + .... + (h_r - c_?)²

  • From high school calculus, you must have learned that to find the maximum/minimum of a function, you take the derivative and find the zero.

    Since S_r depends only on h_r, we find that the derivate is (if it helps, imagine h_r to be "x"):

    S'_r = 2 (h_r - c₁) + 2 (h_r - c₂) + 2 (h_r - c₃) + .... + 2 (h_r - c_p)

  • We find that S'_r = 0, when:
    2 (h_r - c₁) + 2 (h_r - c₂) + 2 (h_r - c₃) + .... + 2 (h_r - c_p) = 0

    or:

    p × h_r = c₁ + c₂ + c₃ + .... + c_p

    thus:

    h_r = (c₁ + c₂ + c₃ + .... + c_p)/p

    h_r = (x_sr + x_sr+1 + x_sr+2 + ... + x_er)/p

  • In other words:
    • The values that will minimize the error in a bucket is the average value for the items in the bucket.

  ---

  ---

• The (minimum) error in a bucket
  • So we have determined that when
    h_r = (x_sr + x_sr+1 + x_sr+2 + ... + x_er)/p

    the error made in bucket b_r is minimized.

  • We still need to compute the error itself...

  • Before I proceed with the derivation, I want to make a change in the indices used, it's too clumpsy. I will write h_r as follows:
    h_r = (x₁ + x₂ + x₃ + ... + x_p)/p

  • The error made in the bucket b_r is given by (see click here) (after replacing the clumpsy index with 1, 2, 3, ..., p):

    Sr = (hr - x1)2 + (hr - x2)2 + (hr - x3)2 + .... + (hr - xp)2 or: Sr = (hr2 - 2hrx1 + x12) + (hr2 - 2hrx2 + x22) + + .... + (hr2 - 2hrxp + xp2) or: Sr = p × hr2 - 2hr × (x1 + x2 + .... + xp) + (x12 + x22 + .... + xp2) or: Sr = p × hr2 - 2hr × p × hr + (x12 + x22 + .... + xp2) or: Sr = p × hr2 - 2p × hr2 + (x12 + x22 + .... + xp2) or: Sr = p × hr2 - 2p × hr2 + (x12 + x22 + .... + xp2) or: Sr = (x12 + x22 + .... + xp2) - p × hr2 or: Sr = (x12 + x22 + .... + xp2) - p × (x1 + x2 + ... + xp)2/(p2) or: Sr = (x12 + x22 + .... + xp2) - (x1 + x2 + ... + xp)2/p Now we replace back the clumpsy notation: Sr = (xsr2 + xsr+12 + .... + xer2) - (xsr + xsr+1 + ... + xer)2/p

  ---

  ---

• Programming Trickt to compute S_r = (x_sr² + x_sr+1² + .... + x_er²) - (x_sr + x_sr+1 + ... + x_er)²/p
  • From the above, we know that we must compute S_r often, and so we must do so efficiently:

  • Notice that we have not found the optimal partitioning of the histogram boundaries yet - i.e., we don't know the optimal buckets.

    (All we know so far is when we are given a certain bucket division of the histogram, we can find the optimal value h_r for each bucket).

    During the process of finding the B>optimal partitioning of the histogram boundaries, we will need to compute the error value S_r for each histogram, and so we must find a way to compute it efficiently.

  • To compute S_r efficiently, we must be able to compute the following 2 subrange sums efficiently:
    • x_sr² + x_sr+1² + .... + x_er²

    • x_sr + x_sr+1 + ... + x_er

  • You need to maintain the following 2 array of values
    • An array P[] where:
      • P[1] = x₁
      • P[2] = x₁ + x₂
      • P[3] = x₁ + x₂ + x₃
      • ...
      • P[k] = x₁ + x₂ + x₃ + ... + x_k

    • An array PP[] where:
      • PP[1] = x₁²
      • PP[2] = x₁² + x₂ ²
      • PP[3] = x₁² + x₂ ² + x₃ ²
      • ...
      • PP[k] = x₁² + x₂ ² + x₃ ² + ... + x_k²

  • Now, if you can find any 2 subrange sums very easily. For example:

    x1 + x2 + ... + x30 = P[30] - P[0] (initialize P[0] = 0) x5 + x6 + ... + x30 = P[30] - P[4] x25 + x26 + ... + x78 = P[78] - P[24] x12 + x2 2 + ... + x302 = PP[30] - PP[0] (initialize PP[0] = 0) x52 + x6 2 + ... + x302 = PP[30] - PP[4] x252 + x26 2 + ... + x782 = PP[78] - PP[24]

  ---

  ---

• Lemma 2: S_[a,b] ≥ S_[a,k] + S_[k+1,b]
  • Lemma 2 in the paper click here shows that any solution using more buckets is better than one that uses less buckets.

  • Lemma 2 says:

    Consider a subrange of number [a..b] (and the corresponding values xa, xa+1, ..., xb) If we use a single-bucket histogram to represent these value, the smallest possible error is S[a,b] If we use a two-bucket histogram to represent these values, then we can split the interval [a..b] into two intervals [a..k] and [k+1..b]. Lemma 2 says that the combined error of a histogram using any two intervals [a..k] and [k+1..b] (i.e., any k) will be less than or equal to the error of a single-bucket histogram.

  • Proof: come see me if you want to see it.

  ---

  ---

• Finding the histogram with the minimum error - Part 2 (bucket boundaries)
  • While finding the optimal value for a bucket can be solved using simple calculus, finding the best boundaries for the buckets require computer science...

  • Jagadish et. al., presented a dynamic programming approach to find the optimal bucket partitioning in this paper: click here

  • The approach is based on the following idea:

  • Suppose we want to find the best histogram for x₁, x₂, x₃, ... x_N that has k buckets

    That histogram must use as the last bucket:

    x_?, x_?+1, x_?+2, ... x_N

    We don't know the range of the "best" last bucket.

  • No problem, if we try every single possible case:
    • Last bucket is: x_N
    • Last bucket is: x_N-1...x_N
    • Last bucket is: x_N-2...x_N
    • ...
    • Last bucket is: x₁...x_N

    we will surely have the bases covered.

  • Furthermore, as the figure above illustrates, a histogram of k buckets consists of a histogram of k-1 buckets plus the last bucket.

    So when we try every possible range for the last bucket, the remaining ranges must be covered by an optimal histogram of k-1 buckets.

  • In other words, we have the following recursive relationship:

    Optimal Histogram for [a,b] using k buckets                     = minx=a..b{ Optimal Histogram of [a..x-1] using k-1 buckets + last bucket is [x..b]}

  • The procedure given above indicates that:
    • In order to find the best histogram for [a..b] using k buckets, we must know the best histogram for every possible subrange [a..x] (x = a..b) using k-1 buckets.

  • This type of algorithm is known as dynamic programming - it is taught in CS171 (I know because I taught CS171 in Fall 2005)

    ---

    ---

    Example: Computes a 2 bucket histogram with the following inputs: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 19

    After processing 1 item (1):

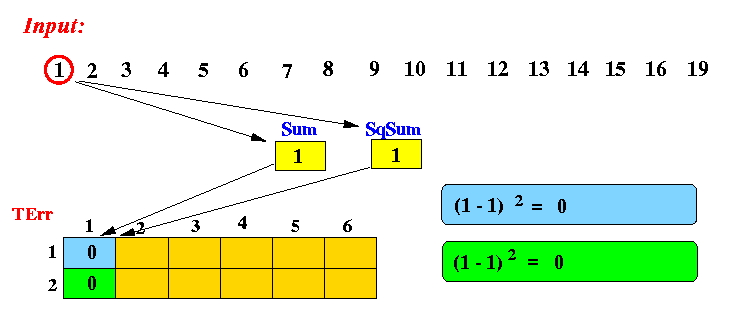
    After processing 2 items (2):

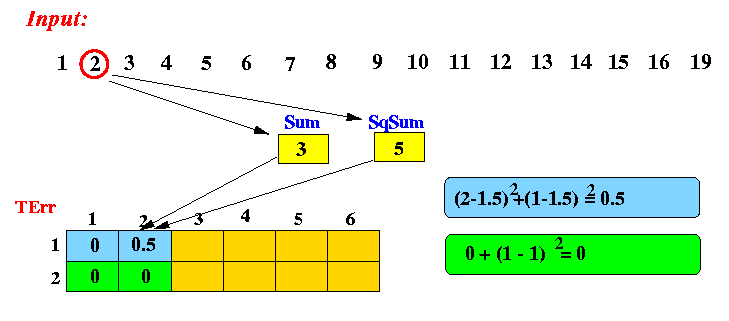
    After processing 3 item (3):

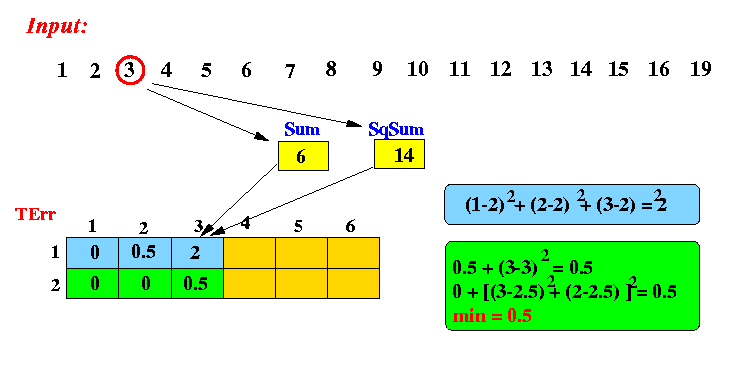
    After processing 4 item (4):

    ---

    ---

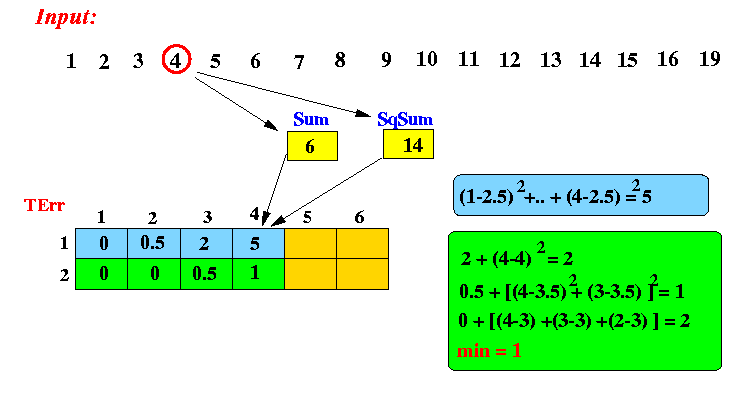
  • Here is the algorithm by Jagadish:

    Procedure V-Opt BestError[i][k] = best error of histogram using k buckets on (1..i) // Squared Error Function: SqError(int a, int b) { s2 = SqSum[b] - SqSum[a]; s1 = Sum[b] - Sum[a]; return (s2 - s1*s1/(b-a+1)); } // Prepare arrays to compute error efficiently Sum[0] = 0; SqSum[0] = 0; for (i = 1; i <= N; i++) { Sum[i] = Sum[i-1] + xi SqSum[i] = SqSum[i-1] + xi2 } // The dynamic algorithm to find the best histogram // // k = # buckets // i = current item - items processed are: (1..i) for (k = 1; k <= B; k++) { // Find optimal histograms for [1..k] for (i = 1; i <= N; i++) { if ( k == 1 ) BestErr[i][k] = SqError(1,i); // Single bucket (easy) else { // Multiple buckets BestError[i][k] = INFINITE; // Start value // Try every possible last bucket for (j = 1; j <= i-1; j++) // Last bucket is [j..i] { if ( BestError[j][k-1] + SqError(j+1,i) < BestError[i][k] ) { BestError[i][k] = BestError[j][k-1] + SqError(j+1,i); } } } } }

  • Example Program: (Demo above code)                        
    • Jagadish's algorithm Prog file: click here
    • A version of Jagadish's algorithm that only prints the min. errors: click here

    • Sample input data file 1: click here
    • Sample input data file 2: click here