- The most time-consuming operation
in Database processing is the:
- join operation.
- The join operation
pairs up tuples from
2 sources based on
key values
in some attribute(s).
- Example:

When a new tuple arrives from stream 1, all tuples in stream 2 must be searched to identify the matching tuples, and vice versa.
- Obviously, it takes a
lot of processing time
to
go through all the tuples...
- If you want to find the
exact answer, there is no shortcut.
You must look through all tuples in the other stream...
- However, often,
all we need is an
approximate answer.
- Example:
- What fraction of econ. students has taken CS170 ?
- What fraction of students who has taken CS170 goes on to take CS171 ?
- The first method
that we will study to
reduce query processing cost
(to meet real time processing requirements) is a simple
statistical technique using
Random Sampling
- Principle of Random Sampling:
- A small
representative (random) sample
is taken from each input.
- The join operation is performed
on the samples
- Results:
- The output will
be much smaller (= different)
than the original result
- Question:
- Is the (different) output
representative
for the
original
(accurate) output ???
- I.e.: we can scale the smaller output to obtain an approximate answer for the original output.
- Is the (different) output
representative
for the
original
(accurate) output ???
- Further question:
- How do you pick s representative sample ???
- The output will
be much smaller (= different)
than the original result
- NOTE: we know that the answer is approximate, and we are willing to sacrifice accuracy for efficiency ...

- A small
representative (random) sample
is taken from each input.
- Random Sample:
- A random sample of r items is obtained by humans by blind-folding someone and ask him/her to pick out r item.
- Different ways to select (random) items:
-
Random Sampling without Replacement
(WoR):
- Pick an item (blind-folded - so every item gets the same chance
on being picked)
do not put the selected item back
- Pick another item
from the remaining ones
(blind-folded - so every remaining item gets the same chance
on being picked), do NOT put the item selected back
- And so on...
Stop when you have selected r items.
- Pick an item (blind-folded - so every item gets the same chance
on being picked)
-
Random Sampling with Replacement
(WR):
- Pick an item, write down its value and
put the item back
- Repeat...
Stop when you have selected r items.
- NOTE:
-
you can select a previously selected item again...
- Pick an item, write down its value and
-
Random Sampling by Independent Coin Flip
(CF):
- Pick out an item
and
flip a coin.
The coin will come up head with some probability f.
If the coin comes up head, then select the item out.
(Otherwise, discard the item. I.e., the same item will not get picked again).
- Repeat for every item in the input until exhausted.
- NOTE:
-
Each item gets selected with
probability f.
The will be approximately f × r items selected
You are not guaranteed to select exactly r items
- Pick out an item
and
flip a coin.
-
Random Sampling without Replacement
(WoR):
- Picking a given number
(r) of tuples from an
input stream
presents a
new problem
in Random Sampling
- Problem description:
- You are given an
input stream of tuples
- You need to
select
r tuples
randomly from the
input stream
You must decide to select the item as the items arrive.
- You are given an
input stream of tuples
- Difficulty of this problem:
- Selecting r tuples
from the input is
easy
if you know in advance
how many tuples there will be
in the input.
- The main difficulty
in this problem is:
- We must not
store every tuple
from the input
(But we do need to store some tuples, just not every tuple)
We want to construct the random sampling by looking at the current input tuple, process that tuple, and disgard it (do not look at it again).
- We do not know in advance how many tuples there will be in the input...
- We must not
store every tuple
from the input
- Selecting r tuples
from the input is
easy
if you know in advance
how many tuples there will be
in the input.
- The paper
"Random Sampling with a Reservoir"
presents an algorithm that constructs
a Random Sample
of r items
from an input stream
without Replacement.
The paper can be obtained here: click here
- Each item
in the input stream
is selected with the
same probability
(i.e., unweighted)
The paper presents more sophisticated algorithms (Algorithm X, Y and Z).
I present the simplest algorithm R which will serve our purpose...
- Uniform WoR Random Sample algorithm:
N = 0; // N = Number of items processed Sample[0..r] is the random sample obtain at the end of the algorithm /* ---------------------------------------------------- Step 1: fill the output with the initial N items ---------------------------------------------------- */ for (j = 0; j < r; j++) { Sample[j] = read_next_tuple(); // Get next tuple from input N++; } /* ------------------------------------------------------ Step 2: replace item with new items probabilistically ------------------------------------------------------ */ while ( not EOF ) { t = read_next_tuple(); // Get next tuple from input N = N+1; // N = total number of items M = TRUNC( N*random() ); // Generate random num [0..(N-1)] // Replace item M is M < r (P[success] = r / N if ( M < r ) { Sample[M] = t; } }
- Claims:
- Let N
= total number items in the
input stream
- r items from
the input stream will be selected
in Sample[0..(r-1)]
- Each item is selected with probability 1/N
- Let N
= total number items in the
input stream
- Proof:
- It should be obvious that
r items will be selected
(assuming that there are at least
r items in the
input stream)
- The xth is selected if
- Mx < r at the
time that
the xth item
arrives
- The (x+1)th, (x+2)th, ... Nth items do not replace the xth item
- Mx < r at the
time that
the xth item
arrives
- These probabilities are:
-
Prob[Mx < r] = r/x
- Prob[
(x+1)th replaces
the xth item] =
(r/(x+1)) * 1/r = 1/(x+1)
Prob[ (x+1)th does not replace the xth item] = = x/(x+1)
- Prob[ (x+2)th replaces the xth item] = (r/(x+2)) * 1/r = 1/(x+2)
Prob[ (x+2)th does not replace the xth item] = = (x+1)/(x+2)
- And so on..
- Prob[ (x+2)th replaces the xth item] = (r/(x+2)) * 1/r = 1/(x+2)
-
Prob[Mx < r] = r/x
- Then:
-
Prob[
xth item selected
and
xth is not replaced by later items] =
= r/x * [ (x/(x+1)) * ((x+1)/(x+2)) * ... * (N-1)/N ]
= r/N
- It should be obvious that
r items will be selected
(assuming that there are at least
r items in the
input stream)
- The following is an algorithm that constructs
a Random Sample
from an input stream
with Replacement.
The algorithm canbe found in the same paper: click here
- Each item
is selected
with the same probability
(i.e., unweighted)
- Note: the
behavior of the
sequential sampling
algorithm on the input stream is as follows:
- It is as if all data items
has arrived already
(and collected in a huge buffer)
- Then r items are selected from the input stream with replacement
- It is as if all data items
has arrived already
(and collected in a huge buffer)
- Uniform WR Random Sample algorithm:
N = 0; // N = Number of items processed while ( not EOF ) { t = read_next_tuple(); // Get next tuple from input N = N+1; // N = current number of tuples for (j = 0; j < r; j++) { // Replace item Sample[j] with probab 1/N if ( random() < 1/N ) { Sample[j] = t; } } }
- The following algorithm that constructs
a
Random Sample
from an input stream using the
coin-toss
method.
- Each item is selected with the same probability f
(i.e., unweighted)
It is very intuitive...
- Uniform CF Random Sample algorithm:
N = 0; // N = Number of items processed NOTE: algorithm will select an avg. of f*N tuples... while ( not EOF ) { t = read_next_tuple(); // Get next tuple from input // Select tuple if coin toss is success... if ( random() < f ) { Sample[N] = t; N = N+1; } }
- The unweighted sampling algorithm
are not useful
in simplifying
join operations
- The main idea
to obtain an approximate solution
for a join operation
requires
that the
sample
represents the original
input data
- Recall the objective of
sampling
is:
- to obtain a smaller, but representative (sub)set of the input.
Example:

- Consider what
could happen
if we use a
uniform random sample
of the input
in a join operation
Example:
- There is one tuple (a1, ..) in R1
- And there are k tuples
(a2, ..) in R1
-
k is very large (say: 1,000,000)
- Conversely: there is one tuple (a2, ..) in R2
- And there are k tuples
(a1, ..) in R2
- The probability
that the tuple (a1, b0)
in R1 is selected
is extremely small !!!
- So also, the
probability
that the tuple
(a2, c0)
in R2 is select
is extremely small !!!
- The
most likely scenario
of a (uniform) sample will be:
- Buffer 1 contains only (a2, ..) tuples
- Buffer 2 contains only (a1, ..) tuples
The join operation will produce no output tuples !!!
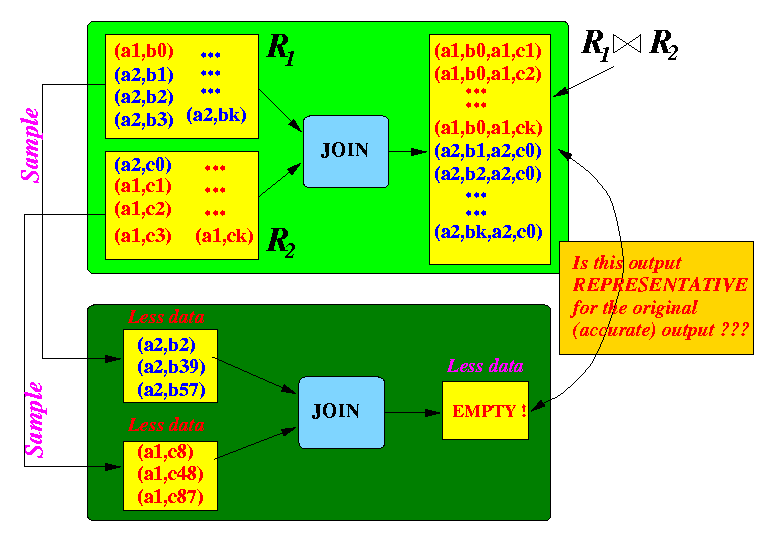
- The result is empty and it is certainly not representative to the original output...
- Consider the distribution
of the tuples in the
input sources
and the
result:
Input 1: Input 2: Output: --------- ---------- ------------ (a1,b0) (a2,c0) (a2,b1) (a1,c1) (a1,b0,a1,c1), (a1,b0,a1,c2), ..., (a1,b0,a1,ck), (a2,b2) (a1,c2) (a2,b1,a2,c0), (a2,b2,a2,c0), ..., (a2,bk,a2,c0) ... ... (a2,bk) (a1,ck)
- The result set of the
join
R1 ▷◁ R2
contains the
source tuple
(a1,b0)
from R1
There is only a single tuple (a1,b0) in R1
- The result set of the
join
R1 ▷◁ R2
contains the
source tuple
(a2,c0)
from R2
There is only a single tuple (a1,b0) in R1
- Observation:
- Tuples in R1 and R2 are not sampled uniformly but weighted
- Weighted by what factor ???
Answer:
- A tuple x from the relation R1 is sampled with a probability that is proportional the number of tuples in R2 that join with x
- A weighted sample
is a random sample where
different items
are selected
with
different probablity
- The following figure illustrates the
difference
between:
- unweighted sampling
of the elements 1, 2, 3, and 4
- weighted sampling of 1, 2, 3 and 4 where Prob[select 1] = 1/2, Prob[select 1] = 1/6, Prob[select 1] = 1/6, and Prob[select 1] = 1/6
Example:
- Because the probablity of selecting 1 is 3 times as high as the other items, it is as if the value 1 is duplicated 3 times in the input set
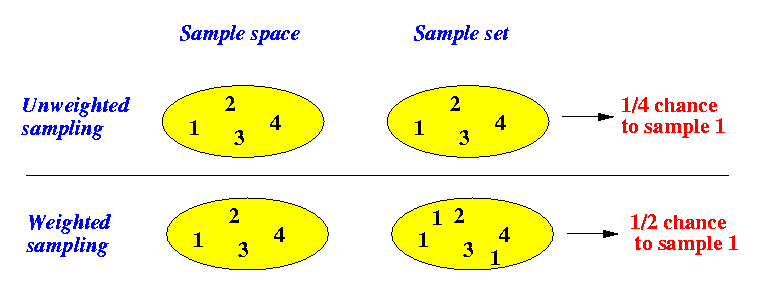
- unweighted sampling
of the elements 1, 2, 3, and 4
- Definition: Weighted Sampling
- Let w(t)
be a non-negative integer
(weight) assigned to
a
tuple t
in a relation R
- A weighted WR (With Replacement) sample from relation R is the same as an unweighted WR sample from a modified relation R* where there are w(t) copies of each tuple t.
- Let w(t)
be a non-negative integer
(weight) assigned to
a
tuple t
in a relation R
- The following algorithm (WR2) constructs a
weighted WR
(With Replacement) sample
from an input stream:
W = 0; // W = Weight while ( not EOF ) { t = read_next_tuple(); // Get next tuple from input W = W + w(t); // Sum of weights so far... for (j = 0; j < r; j++) { if ( random() < w(t)/W ) { Sample[j] = t; } } }
- The algorithm is adapted from the unweighted version (See: click here )
- The weighted sampling algorithm
requires the
weight w(t)
of each tuple
t
- Remember we work with
data streams...
where the input data in the stream may not be known in advance...
- The weight w(t)
of each tuple
t
depends
on the
number of occurences
of the tuple
t
in the input stream...
- Therefore:
- a representative weighted
sample can only be constructed if we
have the
information on the
data distribution
in the input stream...
- The more information we have on the data data distribution, the better the weighted sample we can construct...
- a representative weighted
sample can only be constructed if we
have the
information on the
data distribution
in the input stream...
- The paper
(click here)
distinguishes the following cases:
- No information available
on R1 and
R2:
Naive-Sample
- Index on R1
and
Index/Statistics info. on R2:
Olken-Sample
- has been previously studied by Olken. - No information on R1
and
Index/Statistics info. on R2:
Stream-Sample
- this is new research presented in the paper - No information on R1
and
only Statistics info. on R2:
Group-Sample
- this is new research presented in the paper - No information on R1
and
partial Statistics info. on R2:
Frequency-Partition-Sample
- this is new research presented in the paper
- No information available
on R1 and
R2:
Naive-Sample
xxxxx
- NOTE: the problem we are solving is to obtain a
representative (smaller) set of the output of a join
operation.
- If no information on the inputs R1 and R2
are available, we have seen above that there is no way
we can sample the inputs R1 and R2,
and apply a join operation to get a representative
(smaller) set of the original output...
- If we insist on getting a representative (smaller) set of the output
of a join operation, this is the only way to do it:

- NOTE: F. Olken at Univ. of California, Berkeley had studied this
problem in 1993 as his PhD thesis.
He studied the problem of constructing a sample of a join output when a lot of information on the inputs are available:
- R1 is indexed (look up is fast)
- R2 is indexed and we know statistics (number of occurence) on the different values of the attributes
- According to the paper
(click here)
Olken proposed the following solution
(to obtain a representative sample of the output of a Join operation):
M = largest frequency of the joining attribute (A) values in R2 (remember: we know the statistics !) r = output sample size; NtuplesOutput = 0; while (NtuplesOutput < r) { Sample a tuple t1 ∈ R1, uniformly at random; Sample a random tuple t2 ∈ R2 from among tuples t ∈ R2 that have t.A = t1.A Output tuple t1 * t2 with probability m2(t2.A)/M, and with probaility 1 - m2(t2.A)/M, reject the sample (Not sure what it means, reject one tuple or reject all tuples) NtuplesOutput += number of tuples outputted; } - We will not dwell on Olken sample, because it does not apply to streams.
And we are mostly interested in stream data...
- Suppose we have the following situation:
- No information on R1 available
- R2 is indexed and statistics info. on R2 are available.

- This is the case when R1 is a stream and
R2 is a materialized database.
- A representative sample can be constructed more efficiently as follows:
Use Weighted Sampling algorithm (weights from statistics in R2) to produce a Weighted Sample with Repetition set S1 ⊂ R1 (The weight of sampling w(t) of tuple t is the frequency count of t.A in R2 !!!) (The weighted sampling algorithm will end and produce a set of "r" tuples.) For each output tuple in sample S1 do { let t1 = next tuple in S1; Sample a random tuple t2 &isin R2 among the tuples t &isin R2 that have t.A = t1.A (Note: because R2 is indexed, we can find all tuples t &isin R2 that have t.A = t1.A very easily by using the index !) Output t1 * t2 (join) }
- Suppose we have the following situation:
- No information on R1 available
- R2 is NOT indexed (i.e., we cannot get the individual tuples), but statistics info. on R2 are available (we know how many tuples has A=1, A=2, etc...).

- This is the case when R1 is a stream and
R2 is not a materialized database.
- A representative sample can be constructed efficiently as follows:
Use Weighted Sampling algorithm (weights from statistics in R2) to produce a Weighted Sample with Repetition set S1 ⊂ R1 (The weight of sampling w(t) of tuple t is the frequency count of t.A in R2 !!!) (The weighted sampling algorithm will end and produce a set of "r" tuples.) Let S1 consists of the tuples (s1, sr, ..., sr) For each tuple si &isin S1 do { Compute: Xi = si * R2 // Join tuple si with every tuple in R2 // NOTE: We do this, because R2 is not indexed, // so we can't find tuples in R2 // with a given value t.A quickly Pick 1 tuples from Xi Output the selected tuple }
- Too complicated and not very relevant - skipped...
- I will provide 2 programs:
- Uniform a b: generate uniform numbers between a and b
- Sift a b c: generate Sift distributed numbers, 80% of the numbers will fall between a and b and 20% falls between b and c.
- Implement Naive-Sample Algorithm (to verify results) (1 student)
- Implement Stream-Sample Algorithm (2 student)
- Implement Group-Sample Algorithm (2 student)