- One-pass algorithm:
initialize a search structure H on all attributes of S; /* =========================================================== Phase 1: Use 1 buffer and scan the SMALLER relation first. Build a search structure on the SMALLER relation to help speed up finding common elements. =========================================================== */ while ( S has more data blocks ) { read 1 data block in buffer b; for ( each tuple t ∈ b ) { insert t in H; // Build search structure // (hash table or search tree) } } /* ======================================================== Phase 2: Output only those tuples in R that are also in S We use the search structure H to implement the test t ∈ H efficiently !!! For H, we can use hash table or some bin. search tree ========================================================= */ while ( R has more data blocks ) { read 1 data block in buffer b; for ( each tuple t ∈ b ) { if ( t ∈ H ) { output t; // t in R and S } } }
Buffer utilization using M buffers:
- Phase 1:
partition the M buffers as
follows:
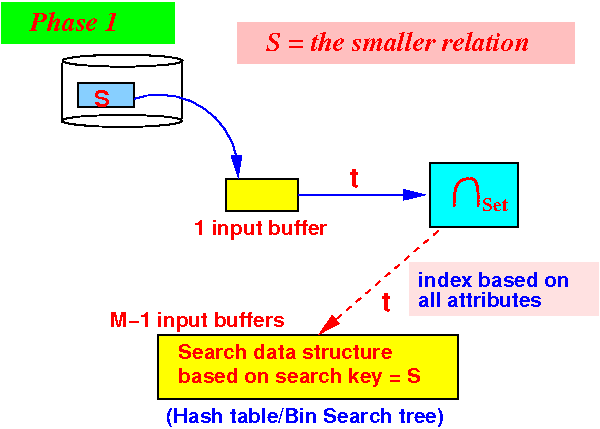
Use 1 buffer for input from S
Use M−1 buffers for the search structure
- Phase 2:
partition the M buffers as
follows:
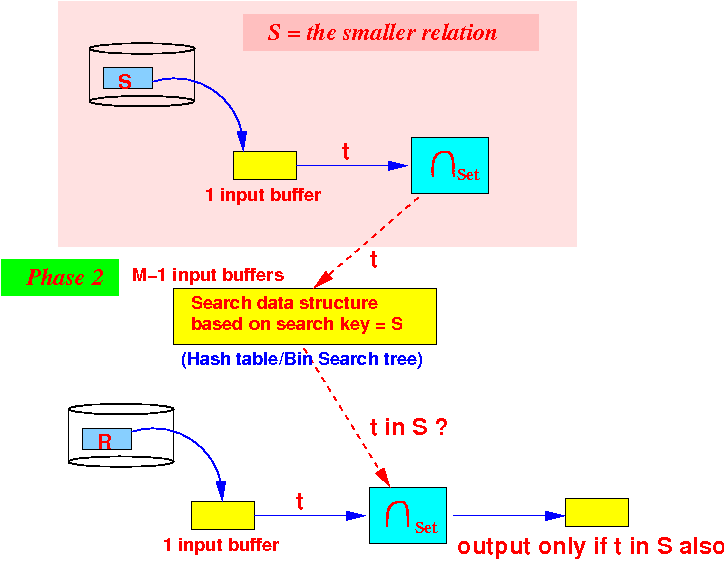
Use 1 buffer for input from R
We are still using M−1 buffers for the search structure in phase 2
- Phase 1:
partition the M buffers as
follows:
- Fact:
- R ∩ S can be
computed on
one processor if:
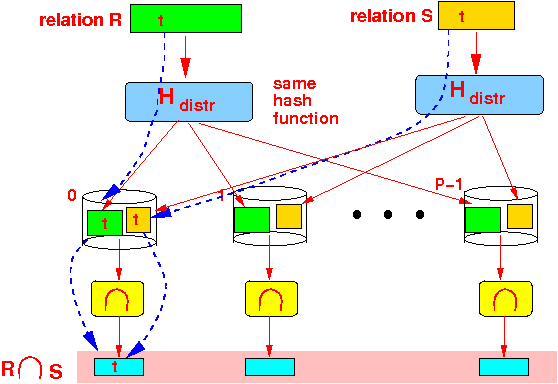
- The same tuple in both R and S are stored (hashed) on the same processsor
- R ∩ S can be
computed on
one processor if:
- Therefore:
- If Hashdistribution used
for relations
R and
S are
same:
- The parallel execution of the uni-processor R ∩ S algorithm will compute the intersection correctly
- Otherwise:
- We must pre-process the (smaller) relation S by re-distributing the tuples in relation S using the Hashdistribution of the relation R
- If Hashdistribution used
for relations
R and
S are
same:
- Parallel algorithm for
R ∩ S when
using
same
hash distribution function:
- Each processor executes
the uni-processor σcond( )
locally on its
fragment of
relation R:
Result:
- The collection (bag) of the output of (at) each processor is the output of R ∩ S
- Each processor executes
the uni-processor σcond( )
locally on its
fragment of
relation R:
- Performance
of the parallel
R ∩ S:
- Assuming that
the hash function will
scatter the
relation R
evenly among
P processors:
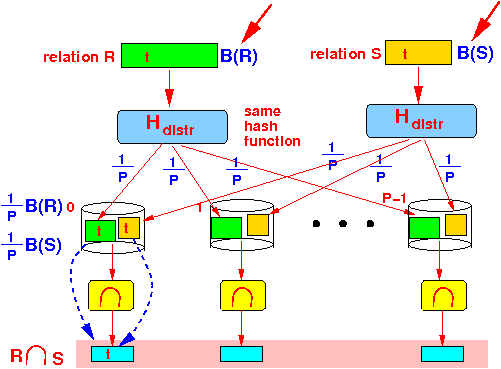
- Each processor will
perform:
1 --- ( B(R) + B(S) ) disk block read operations P
Therefore:
- The parallel
R ∩ S
operation will
- complete in 1/P of the time
- Assuming that
the hash function will
scatter the
relation R
evenly among
P processors:
- Parallel algorithm for
R ∩ S when
using
different
hash distribution function:
- Re-distribute the
tuples of the
the (smaller) relation S :
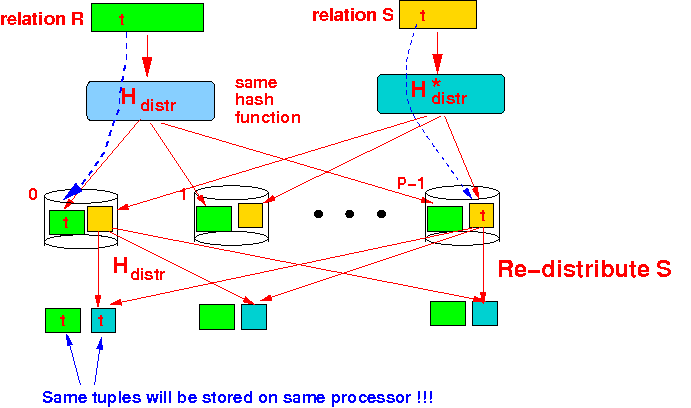
- Each processor executes
the uni-processor σcond( )
locally on its
fragment of
relation R:
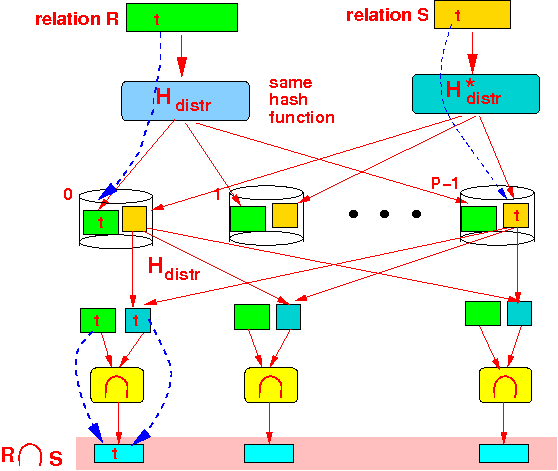
Result:
- The collection (bag) of the output of (at) each processor is the output of R ∩ S
- Re-distribute the
tuples of the
the (smaller) relation S :
- Performance
of the parallel
R ∩ S:
Total amount of work performed: Re-distribute S: Read (re-distribute) relation S: B(S) 1-P Transfer tuples in S: --- B(S) P Write tuples of relation S: B(S) Performing the one-pass intersection: Read R and S: B(R) + B(S) Write tuples in R ∩ S: 0 (not counted)Note:
- Binary
relational algebra operations
sometimes need to use
multi-pass algorithms
- You must adjust the performance computation when a multi-pass algorithm is used.
- Binary
relational algebra operations
sometimes need to use
multi-pass algorithms
- Per processeor
performance:
1 --- ( B(R) + 3 B(S) ) read/write disk block operations P