- Theorem:
- Let S = a schedule for transactions T1, T2, ..., Tn
- Let G = the
precedence graph of
schedule S
- Then:
- The precedence graph G has
no cycles
⇔ (iff)
- Schedule S is conflict-serializable
- The precedence graph G has
no cycles
⇔ (iff)
- Proving the ⇐ part:
- The precedence graph G has
no cycles
⇐
- The schedule S is conflict-serializable
- Reformulated:
If schedule S is conflict-serializable, then
- the precedence graph G has no cycles
- We will prove the
logical inverse
of the statement:
If the precedence graph G has a cycle, then:
- The schedule S is not conflict-serializable,
Proof:
- Given: the
precedence graph G has a
cycle
Suppose the cycle consists of the transactions T1, T2, ..., Tk :
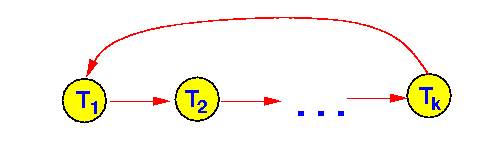
- Then the schedule S
must contains the following
non-swappable actions
in this order:

- In order to make a
serial schedule
(= we need to
group the
operations of
transaction T1), we
must make
one of the following
swaps:
- Swap the
last
op1(X)
forward as follows:

This is not allowed because it swaps the following conflicting operations:
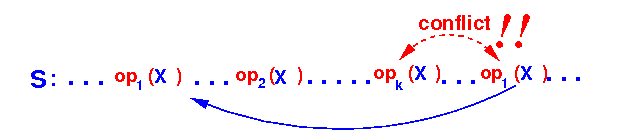
- Swap the
first
op1(X)
backward as follows:
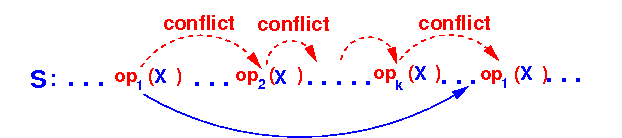
This is also not allowed because it swaps the following conflicting operations:
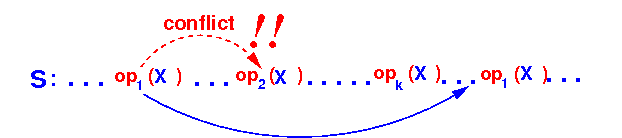
Therefore:
- Schedule S can not be transformed into a serial schedule by swapping non-conflicting actions
In other word (by definition):
- Schedule S is not conflict-serializable
- Swap the
last
op1(X)
forward as follows:
- The precedence graph G has
no cycles
⇐
- Proving the ⇒ part:
- The precedence graph G has
no cycles
⇒
- Schedule S is conflict-serializable
- In other words:
If the precedence graph G has no cycles then
- Schedule S is conflict-serializable
Proof:
- by induction on the number of transactions
Basis: n = 1
- Schedule S is
a schedule of
1 transaction:
T1
- Schedule S is
trivially equal to a
serial schedule !!!
- Schedule S is conflict-serializable !!!
Induction Step:
- Induction assumption:
- If
the precedence graph G
of n transactions
has
no cycles
then (⇒)
- Schedule S of n transactions is conflict-serializable
- If
the precedence graph G
of n transactions
has
no cycles
then (⇒)
- Prove that:
- If
the precedence graph G
of n+1 transactions
has
no cycles
then (⇒)
- Schedule S of n+1 transactions is conflict-serializable
Proof:
- Given: the precedence graph G
of n+1 transactions
has
no cycles
(I.e.: G is a tree !!!)
- Then:
- There is at least
1 node (= root of the tree)
(say: Tk) in
graph G
that has
no ingoing edges:
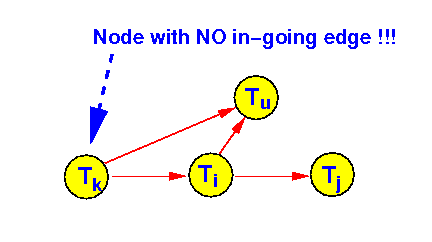
I.e.: Tk "preceeds" all other transactions
That means that we have the following property in the schedule S:
-
Every action (operation) of
Tk
in schedule S is
preceded by
non conflicting actions
from other transactions
Graphically:
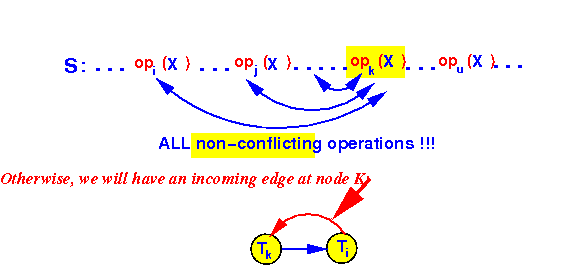
Because:
- Otherwise, there will be an in-going edge to Tk !!!
Therefore, we can move all of the actions of Tk to the front of the schedule:
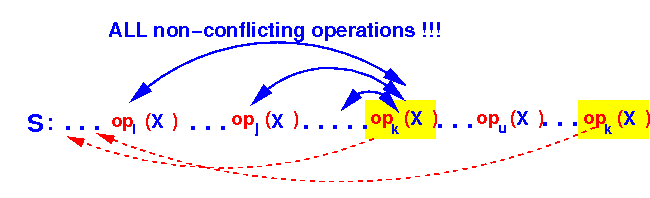
Result:
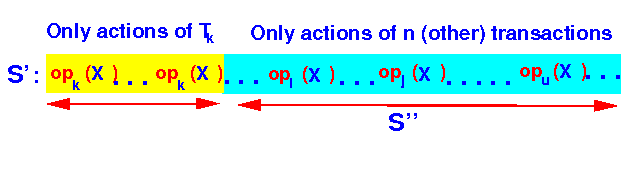
Therefore, schedule S is conflict equivalent to the following schedule:
S "==" Tk ; S'' where: S'' is a schedule of n transactions
- There is at least
1 node (= root of the tree)
(say: Tk) in
graph G
that has
no ingoing edges:
- Furthermore, the
dependency graph for
the schedule S'' is
as follows:
- The original dependency graph
with the node Tk and
all outgoing edgs
removed:
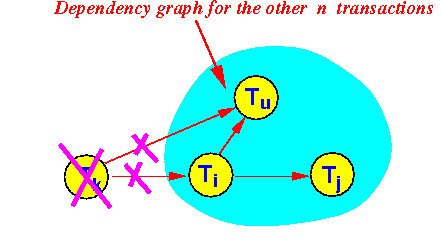
(Because we did not introduce new dependencies nor remove any existing dependency between the other n transactions)
- The original dependency graph
with the node Tk and
all outgoing edgs
removed:
- The dependency graph for
the schedule S''
does not have
cycles:
- Because removing a node Tk and all its outgoing edgs will not create cycles in a graph
So:
- S'' is a schedule of n transactions
- Its dependency graph does not have cycles
By the induction assumption, we conclude that:
- S'' is a conflict-serializable schedule
Therefore:
S "==" Tk ; S'' (from above) S'' is conflict-serializable S'' is conflict-equivalent to some serial schedule
===> S "==" Tk ; Serial Schedule "==" also a Serial Schedule ===> S is conflict-serializable
- If
the precedence graph G
of n+1 transactions
has
no cycles
then (⇒)
- The precedence graph G has
no cycles
⇒