Slideshow:
Why left-deep trees work best for 1-pass algorithms
Claim:
is the best way to execute R ⋈ S ⋈ T ⋈ U when using one-pass algorithm to perform the ⋈ operation
Why left-deep trees work best for 1-pass algorithms
We consider how the query plan will be executed using pipelining to pass results between operators
Why left-deep trees work best for 1-pass algorithms
Initally, all ⋈ operators are active
Why left-deep trees work best for 1-pass algorithms
So operator ⋈3 is now blocked (i.e., it is not active)
Why left-deep trees work best for 1-pass algorithms
So operator ⋈2 is now blocked (i.e., it is not active)
Why left-deep trees work best for 1-pass algorithms
Operator ⋈1 will acquire memory buffers for its execution !!
Why left-deep trees work best for 1-pass algorithms
Remember that memory buffers are premium resources in data processing !!
It's very important that the query execution manage buffer allocation
Why left-deep trees work best for 1-pass algorithms
⋈2 must index all tuples in the build relation before executing phase 2 of the 1 pass algorithm !
So ⋈2 must wait until ⋈1 has finished before starting its phase 2 !
Why left-deep trees work best for 1-pass algorithms
Notice that:
Why left-deep trees work best for 1-pass algorithms
Notice that:
Why left-deep trees work best for 1-pass algorithms
Advantage of left-deep trees execution of 1-pass algorithms: buffer re-use
Why other types of trees are less suitable for 1-pass algorithms
With:
Why other types of trees are less suitable for 1-pass algorithms
Why other types of trees are less suitable for 1-pass algorithms
We must introduce additional synchronization mechanisms to block some ⋈ algorithms !
Why left-deep trees work best for 1-pass algorithms
- Consider the processing steps
of the following
join:
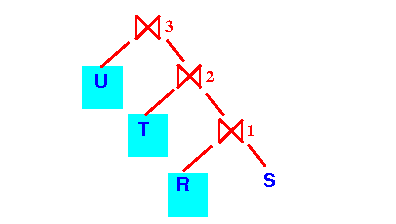
R ⋈ S ⋈ T ⋈ Uusing the one-pass join algorithm.
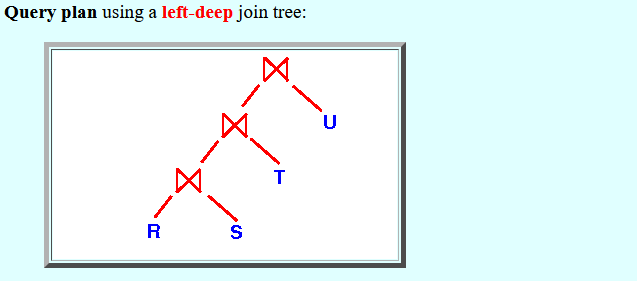
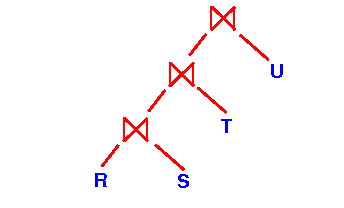
- Processing
R ⋈ S ⋈ T ⋈ U
using a left-deep join tree:
- Query plan using a
left-deep join tree:
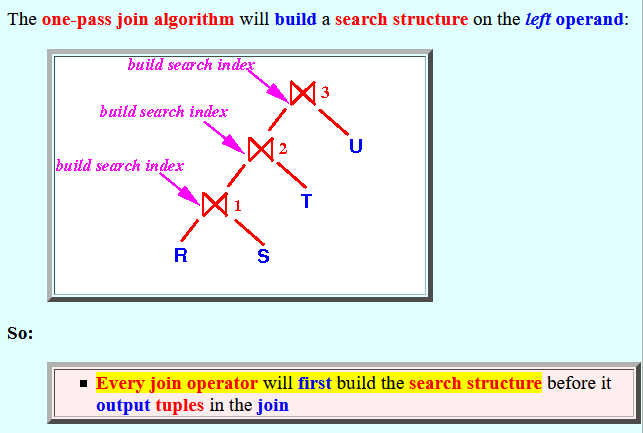
The one-pass join algorithm will build a search structure on the left operand:
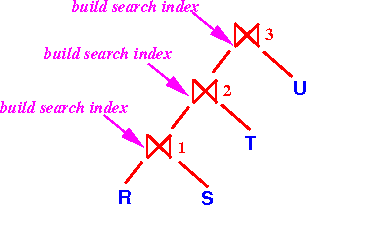
So:
- Every join operator will first build the search structure before it output tuples in the join
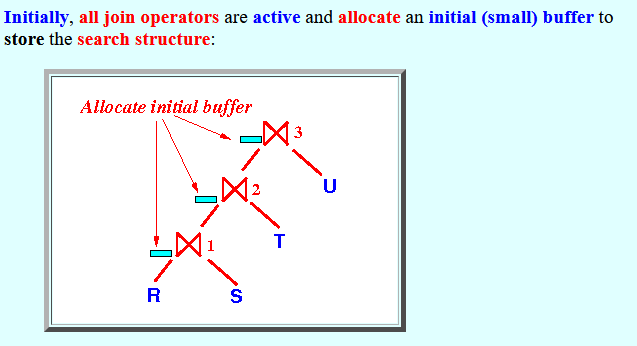
- Initially,
all join operators are
active and
allocate an
initial (small) buffer to
store the
search structure:
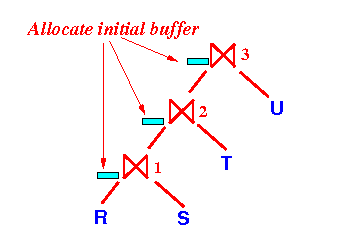
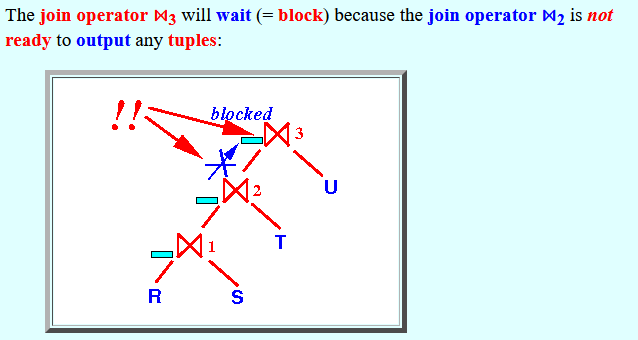
- The join operator ⋈3
will wait
(= block) because
the join operator ⋈2
is not ready to
output any
tuples:
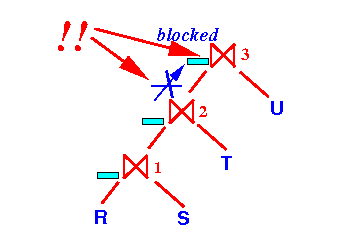
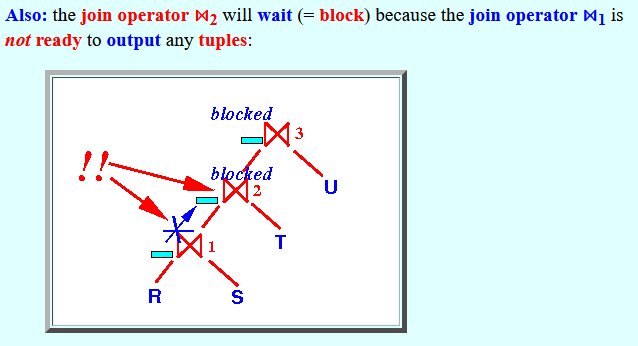
Also: the join operator ⋈2 will wait (= block) because the join operator ⋈1 is not ready to output any tuples:
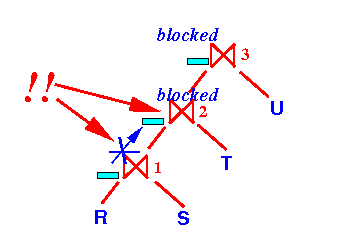
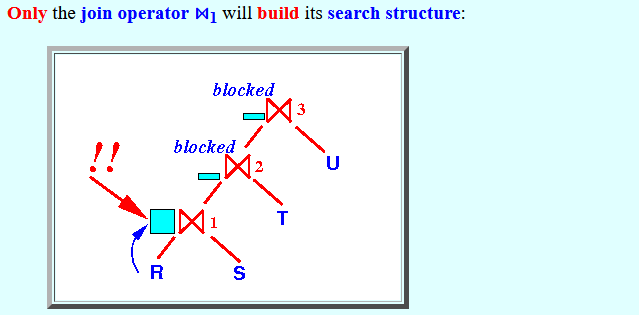
Only the join operator ⋈1 will build its search structure:
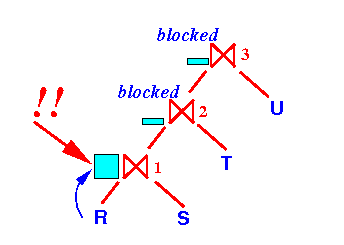
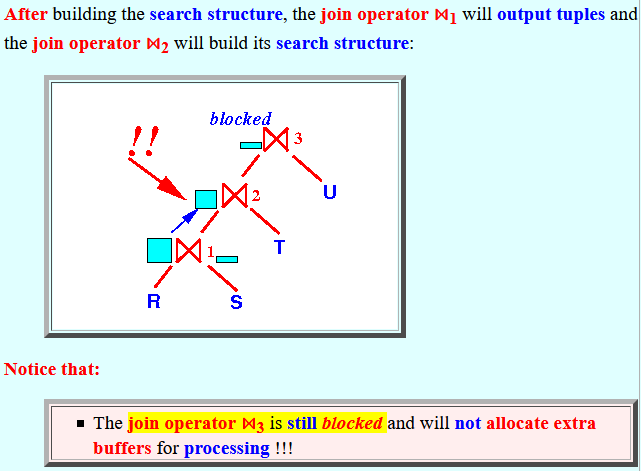
- After building the
search structure,
the
join operator ⋈1 will
output tuples and
the join operator ⋈2 will
build its
search structure:
Notice that:
- The join operator ⋈3 is still blocked and will not allocate extra buffers for processing !!!
-
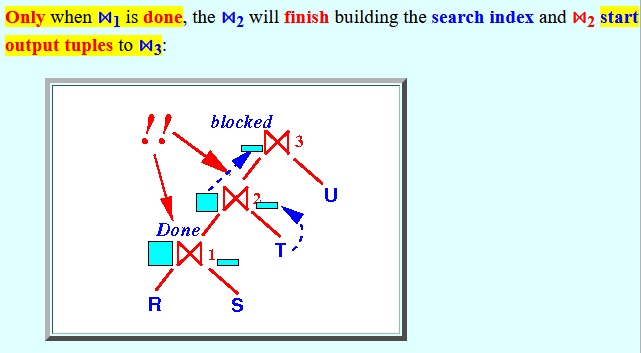
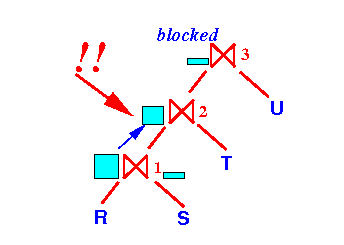
Only when
⋈1 is
done,
the
⋈2
will
finish
building the search index and
⋈2
start
output tuples
to ⋈3:
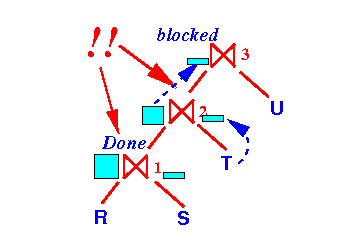
Notice that:
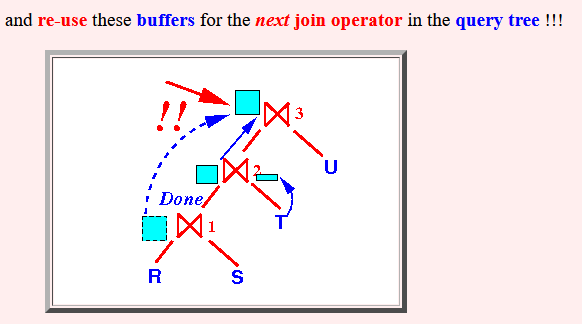
- We can free (= de-allocate) the
buffers used by
the join operator ⋈1
now:
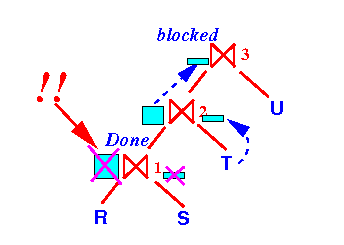
and re-use these buffers for the next join operator in the query tree !!!
- We can free (= de-allocate) the
buffers used by
the join operator ⋈1
now:
- Query plan using a
left-deep join tree:
- Conclusion:
- In
a left-deep join tree:
- When ⋈2 begins to execute the join operation (= generate output tuples), the buffers used in ⋈1 can be re-used
- An similarly:
- When ⋈3 begins to execute the join operation (= generate output tuples), the buffers used in ⋈2 can be re-used
And so on !!!
Because query processing is memory-bound operation:
-
Re-using of
memory buffers
between operators in the
same query plan will
increase the
processing capacity !!!
(I.e.: we can handle larger relations)
- In
a left-deep join tree:
- Now consider the
processing of
R ⋈ S ⋈ T ⋈ U
using a another type of join tree
(e.g., a
right-deep join tree)
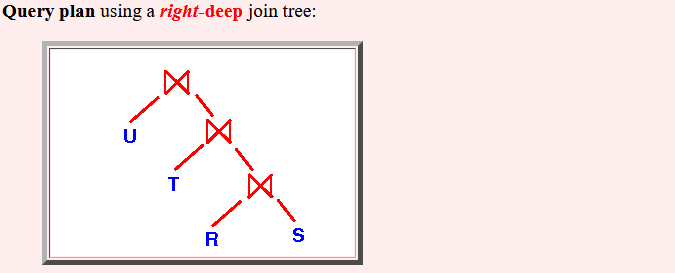
- Query plan using a
right-deep join tree:
- Phase 1 of the
one-pass algorithm is:
- Build a
search index for the
left operand:
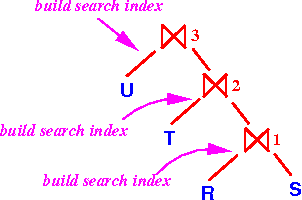
Because each left operand is a relation, all the join operators will be able to read tuples from the relation and build their index !!!
- Build a
search index for the
left operand:
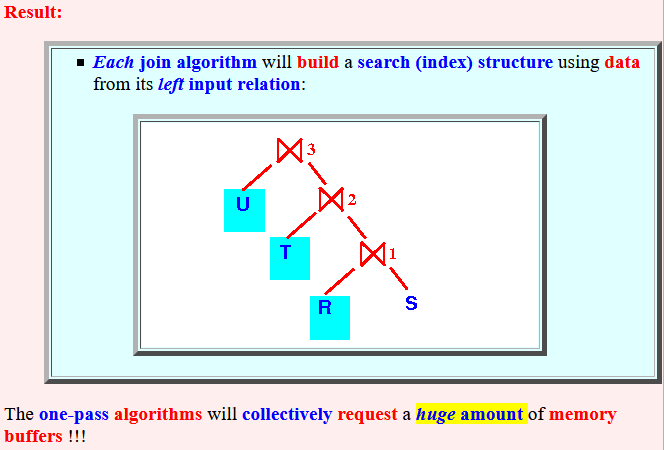
- Result:
- Each join algorithm will
build a
search (index) structure using
data from its
left input relation:
The one-pass algorithms will collectively request a huge amount of memory buffers !!!
- Each join algorithm will
build a
search (index) structure using
data from its
left input relation:
- Query plan using a
right-deep join tree:
- Conclussion:
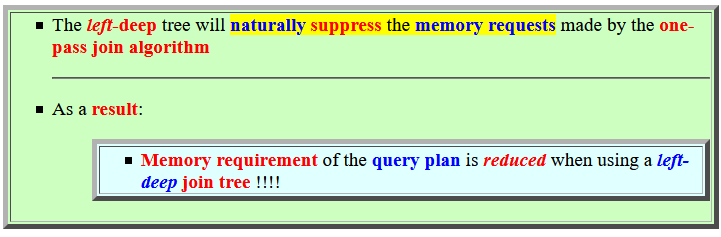
- The left-deep tree
will
naturally
suppress
the memory requests
made by
the one-pass join algorithm
- As a result:
- Memory requirement of the query plan is reduced when using a left-deep join tree !!!!
- The left-deep tree
will
naturally
suppress
the memory requests
made by
the one-pass join algorithm