Slideshow:
- Initialization:
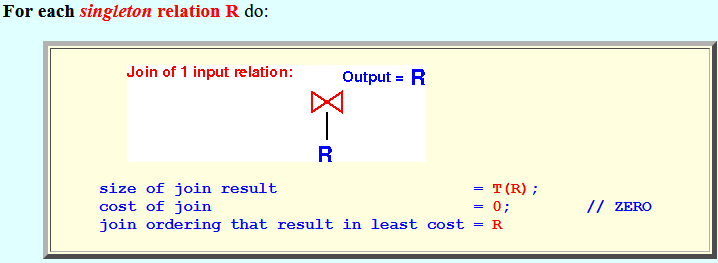
- For each
singleton relation R do:
 size of join result = T(R);
cost of join = 0; // ZERO
join ordering that result in least cost = R
size of join result = T(R);
cost of join = 0; // ZERO
join ordering that result in least cost = R
Example:
- For each
singleton relation R do:
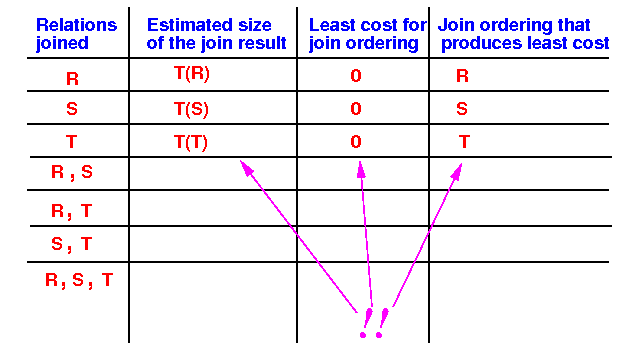
- The first iteration of
the dynamic programming algorithm is
very straightforward
to compute:
- The result of
the join of
Ri ⋈ Rj
is as follows:
 T(Ri) × T(Rj)
size of join result = ---------------------
max(V(Ri,A), V(Rj,A))
cost of join = 0; // because there is
// no intermediate result !!!
join ordering that
result in least cost = Ri ⋈ Rj if T(Ri) ≤ T(Rj)
= Rj ⋈ Ri if T(Rj) ≤ T(Ri)
T(Ri) × T(Rj)
size of join result = ---------------------
max(V(Ri,A), V(Rj,A))
cost of join = 0; // because there is
// no intermediate result !!!
join ordering that
result in least cost = Ri ⋈ Rj if T(Ri) ≤ T(Rj)
= Rj ⋈ Ri if T(Rj) ≤ T(Ri)
Example:
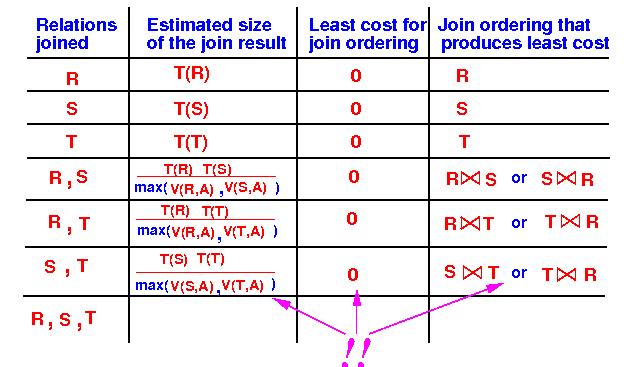
- The result of
the join of
Ri ⋈ Rj
is as follows:
- Note:
- If we need to optimize the join of 2 input relations, we have found the optimal solution !!
- Dynamic Programing Algorithm in
English:
- Use the optimal solution for
joins using
≤ 2 relations to:
- Find the optimal solution for joins using ≤ 3 relations
- Then:
use the optimal solution for
joins using
≤ 3 relations to:
- Find the optimal solution for joins using ≤ 4 relations
- Then:
use the optimal solution for
joins using
≤ 4 relations to:
- Find the optimal solution for joins using ≤ 5 relations
- And so on....
- Use the optimal solution for
joins using
≤ 2 relations to:
- Pseudo code:
N = # relations in the join problem (R1,R2,...,RN) /* =================================================== k = # relations in the join expression (We build the size k up one by one) =================================================== */ for ( k = 3, 4, ...., N ) do { /* ======================================================== Visualize help: if k = 4 then Φ = { {R1,R2,R3,R4}, {R1,R2,R3,R5}, .... ======================================================== */ for ( each subset Φ of size k ) do { /* ====================================== Initilaize (assume some minimum cost) ====================================== */ minCost = ∞; // minCost to join the setset relations in Φ optSol = ∅; // Best join ordering (left-deep join tree) /* -------------------------------------------- Try each possible relation Ri as the last relation in left-deep join tree ⋈ / \ opt Si Ri <-- Try each relation Ri here (opt Si can be found in data structure !) -------------------------------------------- */ for ( each elem Ri ∈ Φ ) do { Si = Φ − Ri // Notice that: // the optimal join order on S has already been computed !!! Cost(Ri) = cost of this (left-deep) join tree ⋈ / \ opt Si Ri <-- Try each relation Ri here if ( Cost(Ri) < minCost ) { minCost = Cost(Ri); optSol = ⋈ / \ opt Si Ri } } /* =============================================== Now we found the lowest cost for the join order for the list of relations Φ =============================================== */ Enter minCost in the Least cost column Enter optSol in the order column Compute the estimate join size and enter } }We will see a worked-out example in the next webpage.