Slideshow:
Estimating the size of the result set
R ⋈ S
Problem description:
Estimating the size of the result set
R ⋈ S
Some possible outcomes:
Estimating the size of the result set
R ⋈ S
Some possible outcomes:
Simplifying assumption 1:
value set containment assumption
The containment of value sets assumption:
Simplifying assumption 2:
value set perservation assumption
The preservation of value sets assumption:
- Given:
- R(X,Y)
- S(Y,Z)
- T(X,Y,Z) = R(X,Y) ⋈ S(Y,Z)
Question:
- Estimate the size of T(X,Y,Z)...
- Possible outcomes of
R(X,Y)
⋈
S(Y,Z)
:
- If the Y attribute values
in
R(X,Y)
and
S(Y,Z)
are
disjoint:
- T( R(X,Y) ⋈ S(Y,Z) ) = 0
- If Y attribute
is a key in
S:
- T( R(X,Y) ⋈ S(Y,Z) ) = T(R)
- If every tuple
in R and
S has the
same Y attribute value:
- T( R(X,Y) ⋈ S(Y,Z) ) = T(R) × T(S)
- If the Y attribute values
in
R(X,Y)
and
S(Y,Z)
are
disjoint:
- Range of
T( R ⋈ S ):
0 ≤ T( R ⋈ S ) ≤ T(R)×T(S)
- Fact:
- Without any assumptions on the joining attribute values, it is not possible to provide an estimation on the result T(R ⋈ S)
- Assumptions that helps
use find an
estimate of
R(X,Y)
⋈
S(Y,Z)
:
- The containment of
value sets
assumption:
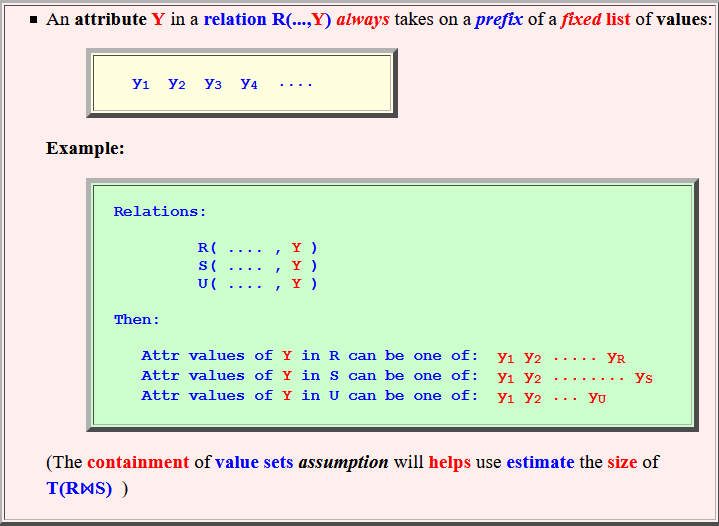
- An attribute Y in a
relation R(...,Y)
always
takes on a prefix
of a fixed list of
values:
y1 y2 y3 y4 ....Example:
Relations: R( .... , Y ) S( .... , Y ) U( .... , Y ) Then: Attr values of Y in R can be one of: y1 y2 ..... yR Attr values of Y in S can be one of: y1 y2 ........ yS Attr values of Y in U can be one of: y1 y2 ... yU(The containment of value sets assumption will helps use estimate the size of T(R⋈S) )
- An attribute Y in a
relation R(...,Y)
always
takes on a prefix
of a fixed list of
values:
- The preservation of
value sets
assumption:
- The join operation
R(X,Y)
⋈
S(Y,Z)
will
preserve
all the
possible values of
the non-joining attributes
In other words:
- The attribute values taken on by X in R(X, Y) ⋈ S(Y,Z) and R(X, Y) are same
- The attribute values taken on by Z in R(X, Y) ⋈ S(Y,Z) and S(Y, Z ) are same
(The preservation of value sets assumption will helps use estimate the size of T(R⋈S⋈U) )
- The join operation
R(X,Y)
⋈
S(Y,Z)
will
preserve
all the
possible values of
the non-joining attributes
- The containment of
value sets
assumption: