---

One-pass Algorithm for ∪_S

---

---

---

 

Slideshow:

The set union (∪_S) operator
 
Note: search (hash) structure need only record the presence of a key
Note: the output contains all tuples in the one input relation + addition tuples in the other relation
The set union (∪_S) operator

The one-pass set union (∪_S) algorithm - Assumptions
 
The one-pass set union (∪_S) algorithm - phase 1

The one-pass set union (∪_S) algorithm - phase 2

The one-pass set union (∪_S) algorithm - phase 1
 
Phase 1 constructs a search (hash) structure using the smaller input relation S.
Phase 1 will output all tuples in S
The one-pass set union (∪_S) algorithm - phase 2
 
Phase 2 re-uses the 1 input buffer to scan input relation R
Phase 2 will output a tuple ∈ R only if the tuple is not found in the search structure
IO cost and buffer requirement for ∪_S
 
❮ ❯



---

---

---

---

• Set Union ∪_S
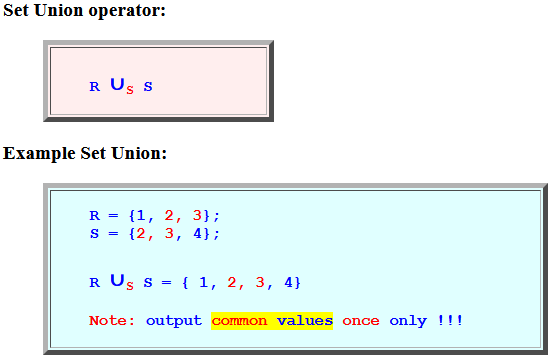
  • Set Union operator:

    R ∪S S

  • Example Set Union:

    R = {1, 2, 3}; S = {2, 3, 4}; R ∪S S = { 1, 2, 3, 4} Note: output common values once only !!!

    Important observation:

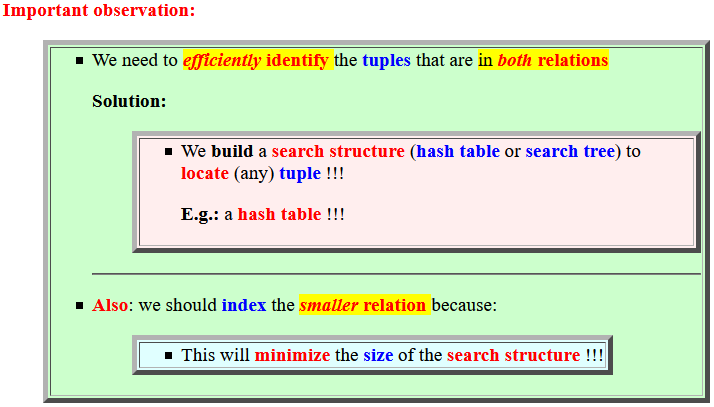
    We need to efficiently identify the tuples that are in both relations Solution: We build a search structure (hash table or search tree) to locate (any) tuple !!! E.g.: a hash table !!! Also: we should index the smaller relation because: This will minimize the size of the search structure !!!

    ---

    ---

  • One-pass algorithm:

    Assumption:

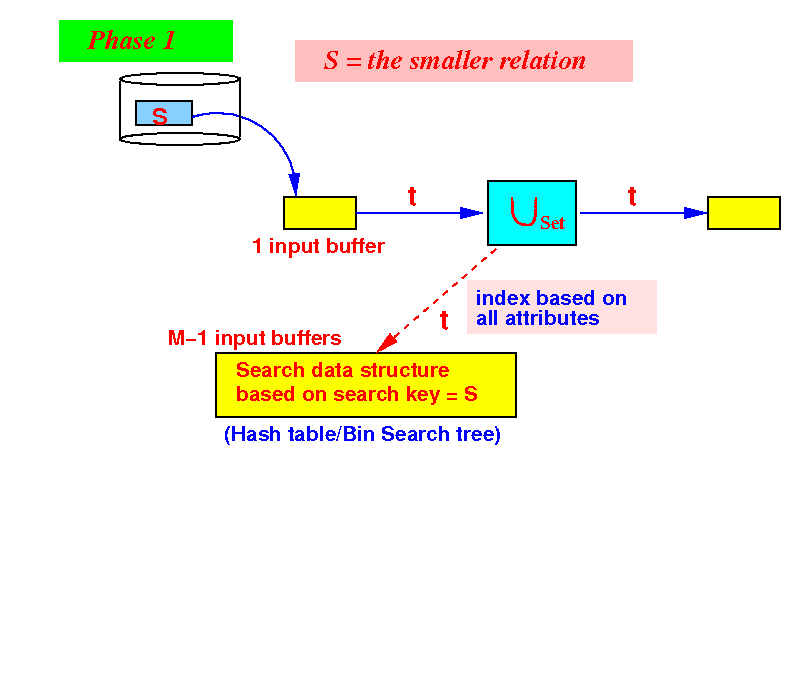
    The input relations are sets.... I.e.: No duplicates in the input !!! The output must be a set !!! I.e.: No duplicates in the output !!! The relation S is the smaller relation Building a search structure using S will minimize the memory requirement

    Algorithm:

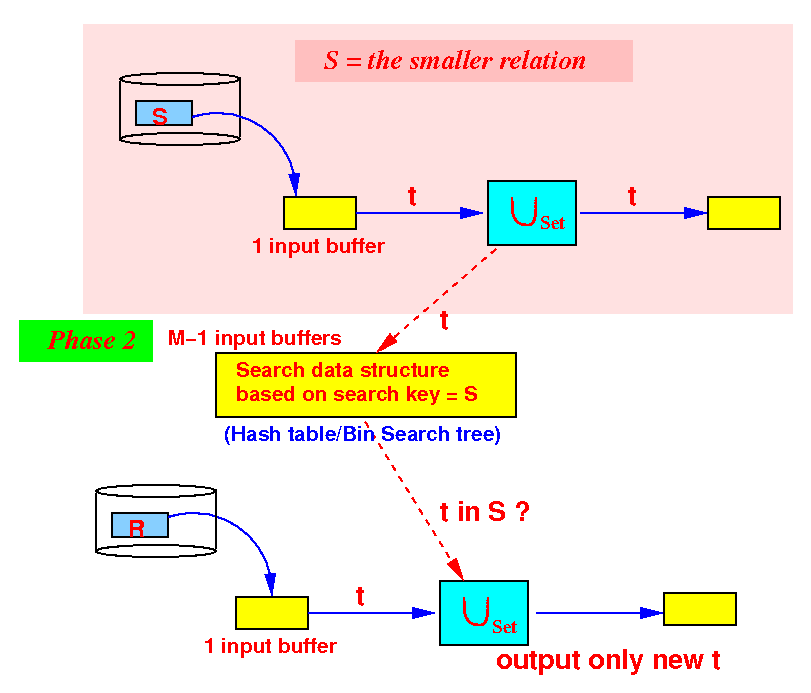
    initialize a search structure H on all attributes of S; /* =========================================================== Phase 1: Use 1 buffer and scan the SMALLER relation first. Build a search structure on the SMALLER relation to help speed up removal of duplicates. Because R ∪S S contains S: we output every tuples in S =========================================================== */ while ( S has more data blocks ) { read 1 data block in buffer b; for ( each tuple t ∈ b ) { insert t in H; // Build search structure // (hash table or search tree) output t; // S is part of the union. } } /* ======================================================== Phase 2: Output only those tuples in R that are NOT in S We use the search structure H to implement the test t ∈ H efficiently !!! For H, we can use hash table or some bin. search tree ========================================================= */ while ( R has more data blocks ) { read 1 data block in buffer b; for ( each tuple t ∈ b ) { if ( t ∈ H ) { /* ----------------------------------- This tuples was in S, duplicate ! ----------------------------------- */ discard t; // I.e.: do not output t } else { output t; // We do not need to insert t in H // because R is a set !!! } } }

    Buffer utilization when there are M buffers available:

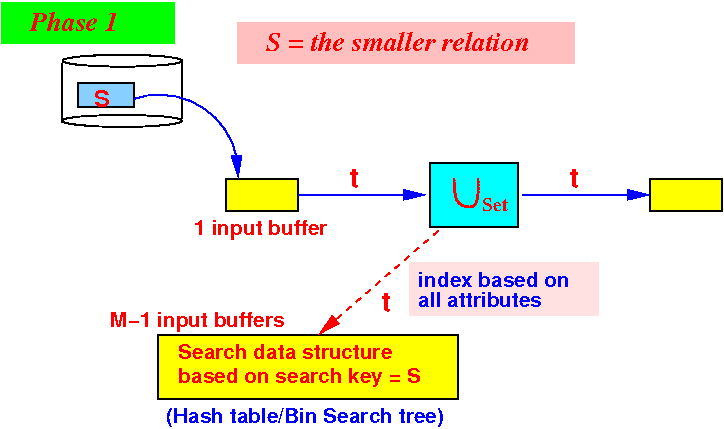
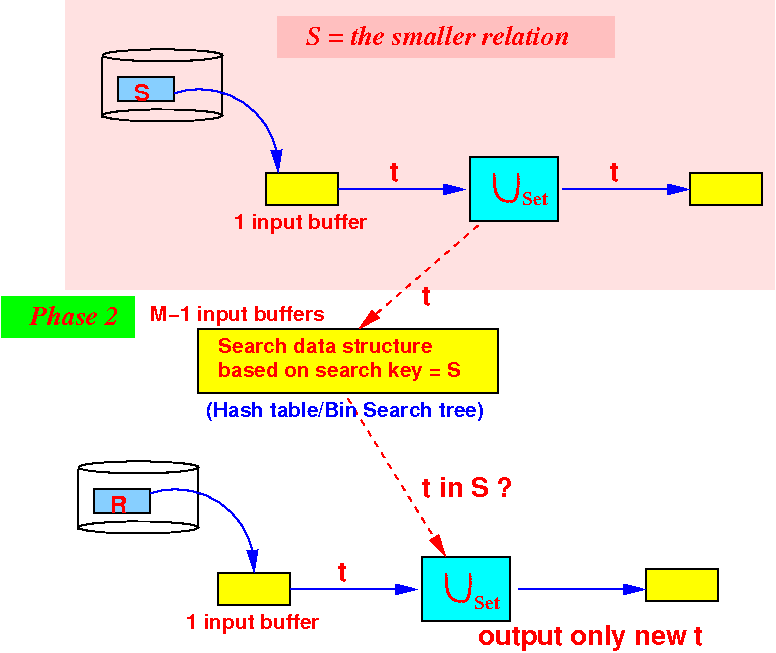
    Phase 1: partition the M buffers as follows: Use 1 buffer for input from S Use M−1 buffers for the search structure Phase 2: partition the M buffers as follows: Use 1 buffer for input from R We are still using M−1 buffers for the search structure in phase 2

  ---

  ---

  ---

  ---

• Cost Analysis for ∪
  • # disk I/O used:

    We read R and S once: B(R) + B(S) --- if the relations R and S are clustered

    ---

  • Memory requirement:

    M ≥ B(S) + 1 buffer            Because we must store a search structure on all tuples in S !!! Relation S is the smaller relation in the union (to minimize the buffer requirement !!)