Slideshow:
The set intersection (∩s) operator
Note: search (hash) structure need only record the presence of a key (see teaching note in this webpage)
However: we can use the ∩B algorithm to compute ∩S !
The set intersection (∩s) operator
- assumptions
In the slide presentation, I will use the ∩B algorithm to compute ∩S...
The one-pass
set intersection (∩s) algorithm
- Example
{a,b,c,e} ∩S {b,c,d}:
Phase 1: read S and build search index with (key, #occurence)
The one-pass
set intersection (∩s) algorithm
- Example
{a,b,c,e} ∩S {b,c,d}:
Phase 2: read R and decrement the search key count; output the key if count > 0
The one-pass
set intersection (∩s) algorithm
- Example
{a,b,c,e} ∩S {b,c,d}:
Phase 2: a ∉ search structure → discard a
The one-pass
set intersection (∩s) algorithm
- Example
{a,b,c,e} ∩S {b,c,d}:
Phase 2: count(b) > 0 → output b (and decrement count(b) is optional because b is unique in set !)
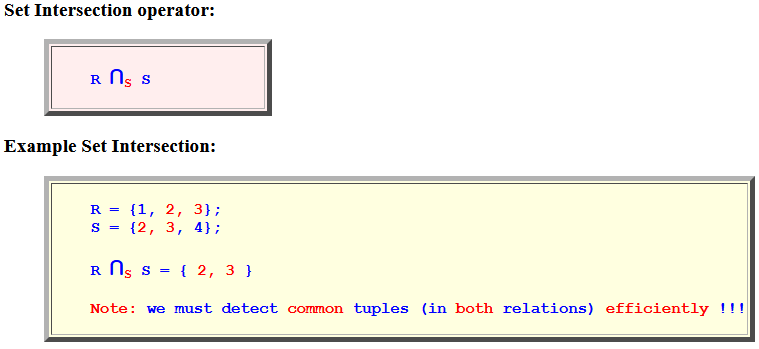
- Set Intersection operator:
R ∩S S - Example Set Intersection:
R = {1, 2, 3}; S = {2, 3, 4}; R ∩S S = { 2, 3 } Note: we must detect common tuples (in both relations) efficiently !!!
- One-pass algorithm:
Assumption:
- The input relations
are
sets....
- The relation S is
the
smaller relation
- Building a search structure using S will minimize the memory requirement
Algorithm:
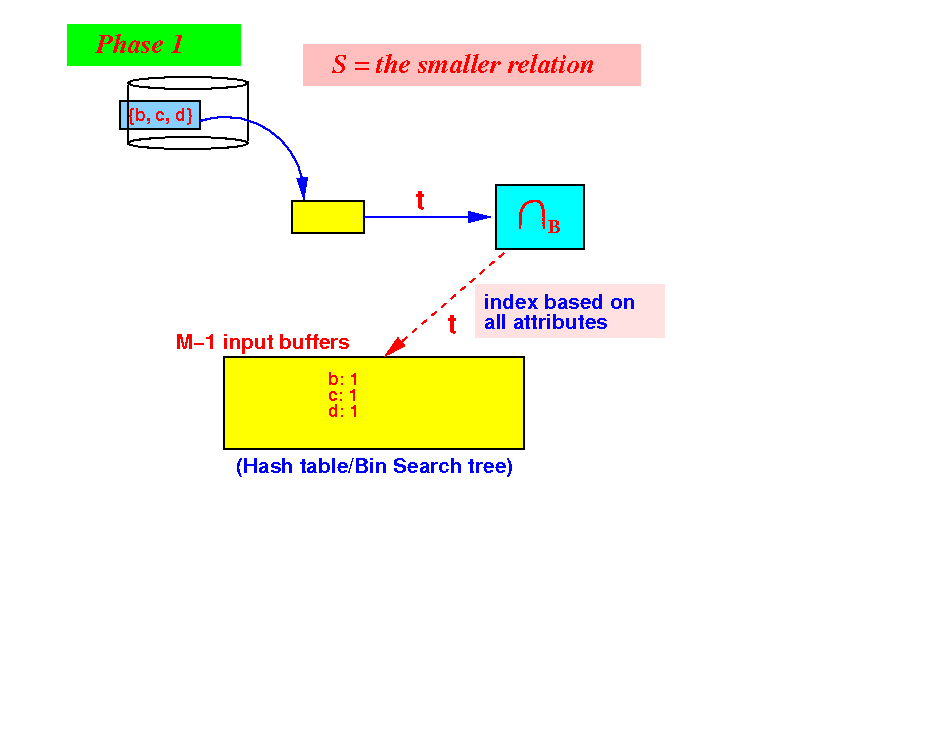
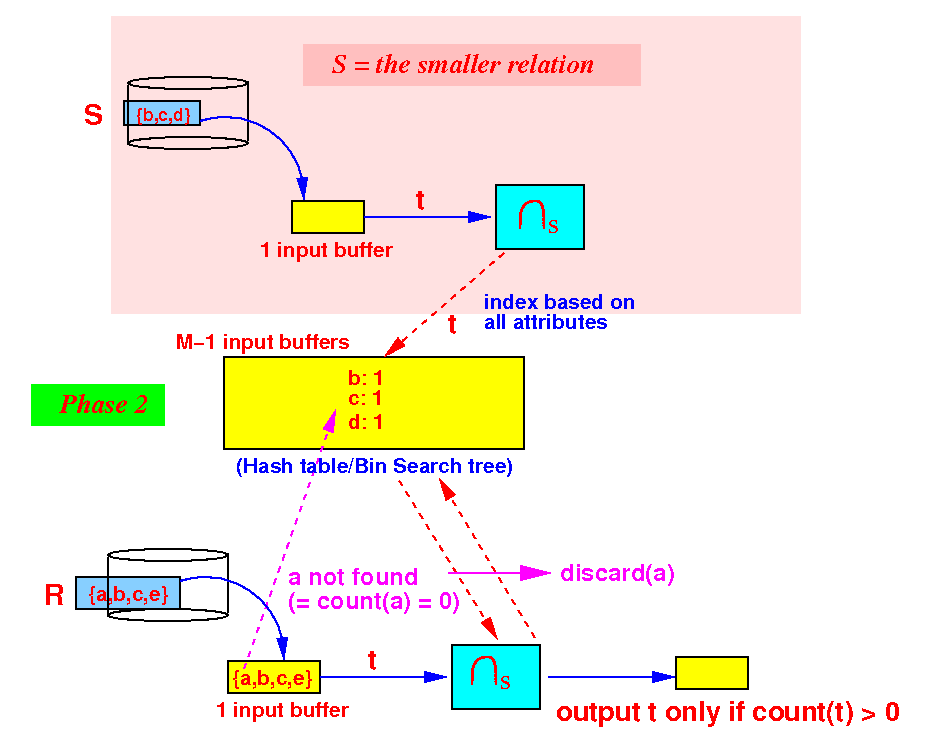
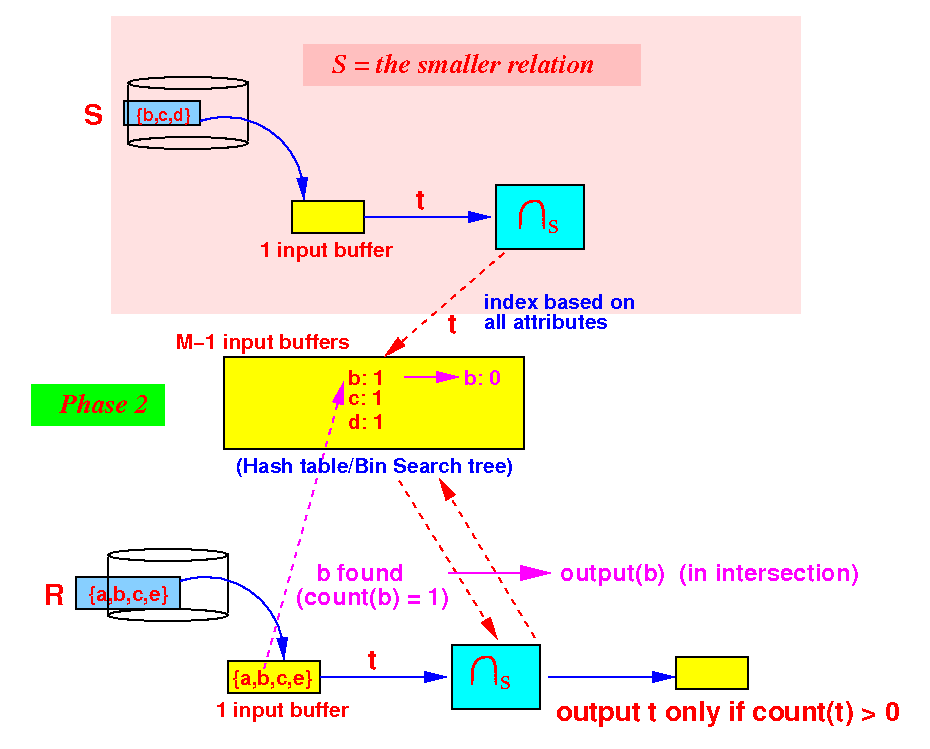
initialize a search structure H on all attributes of S; /* =========================================================== Phase 1: Use 1 buffer and scan the SMALLER relation first. Build a search structure on the SMALLER relation to help speed up finding common elements. =========================================================== */ while ( S has more data blocks ) { read 1 data block in buffer b; for ( each tuple t ∈ b ) { insert t in H; // Build search structure // (hash table or search tree) } } /* ======================================================== Phase 2: Output only those tuples in R that are also in S We use the search structure H to implement the test t ∈ H efficiently !!! For H, we can use hash table or some bin. search tree ========================================================= */ while ( R has more data blocks ) { read 1 data block in buffer b; for ( each tuple t ∈ b ) { if ( t ∈ H ) { output t; // t in R and S } } }
Buffer utilization when there are M buffers available:
- Phase 1:
partition the M buffers as
follows:
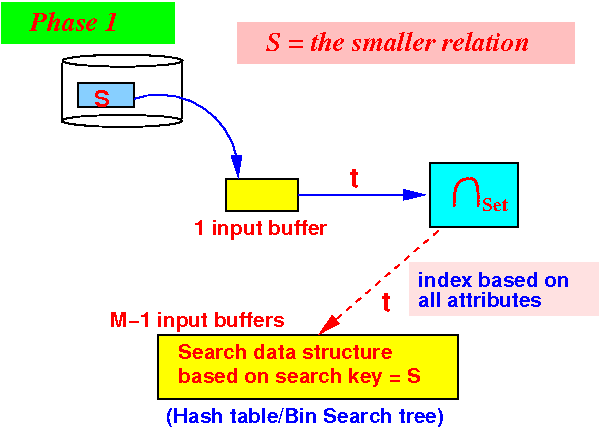
Use 1 buffer for input from S
Use M−1 buffers for the search structure
- Phase 2:
partition the M buffers as
follows:
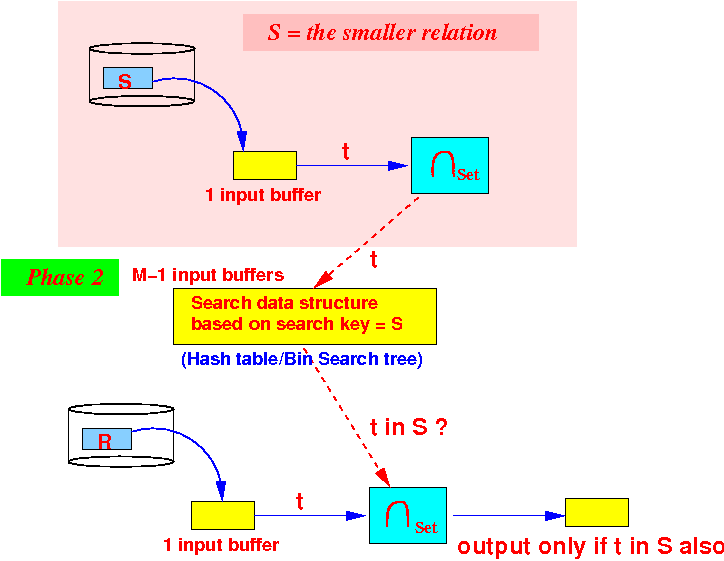
Use 1 buffer for input from R
We are still using M−1 buffers for the search structure in phase 2
- The input relations
are
sets....
- # disk I/O used:
- B(R) + B(S) --- if the relations R and S are clustered
- Memory requirement:
- M ≥ B(S) + 1 buffer
- Relation S is the smaller relation in the intersection
- M ≥ B(S) + 1 buffer