---

One-pass Algorithm for γ

---

---

---

 

Slideshow:

The grouping operator (γ)

The one-pass grouping algorithm (γ)

The one-pass grouping algorithm (γ) - Example
Initial state: group by attr 1 and find max(2nd attr) for each group

 
The one-pass grouping algorithm (γ) - Example
Process next block of data: (read disk block into buffer)

 
The one-pass grouping algorithm (γ) - Example
Process next block of data: (process first tuple)

Find(a): not found → insert(a, max=3) in search structure
The one-pass grouping algorithm (γ) - Example
Process next block of data: (process second tuple)

Find(b): not found → insert(b, max=5) in search structure
The one-pass grouping algorithm (γ) - Example
Process next block of data: (process third tuple)

Find(a): found → update(a, max=7) in search structure
And so on....    After procssing all tuples, we can output the statistic (=max)
Buffer utilization
How to assign buffers when there are M buffers avialable:
   
IO cost and buffer requirement for γ

Note: V(R, [A1, A2, .., An]) = # distinct values in the attributes [A1, A2, .., An]
❮ ❯



---

---

---

---

• Grouping γ
  • Grouping operator:

    γL ( R )

    Note: L can be one of the following functions:

    min   (find the minimum value in each group max   (find the maximum value in each group count   (find the cardinality (# members) in each group sum   (find the sum (of some attribute value) in each group avg   (find the average (of some attribute value) in each group

  • Example Grouping:

    R = (x,y) R = { (a,2), (a,3), (b,1), (b,3) } γavg(y) ( R ) = { (a, 2.5), (b, 2.0) }

    ---

    ---

  • One-pass algorithm:

    initialize a search structure H on grouping attributes of γ; /* ========================================================= Process the statistics for each group ========================================================= */ while ( R has more data blocks ) { read 1 data block in buffer b; for ( each tuple t ∈ b ) { /* ===================================================== We need a search structure H to implement the test t ∈ H efficiently !!! We can use hash table or some bin. search tree ====================================================== */ if ( t ∈ H ) { Update the statistics for group(t); } else { insert t in H; Initialize the statistics for group(t); } } } /* ========================================================= Now we can output the aggregate function for each group ========================================================= */ for ( each group ∈ H ) { Output group search key + statistics; }

    The statistics depends on the aggregate function applied:

    Aggregate function Statistics --------------------------------------------------------------- min current min value in each group max current max value in each group count current size of each group sum current running sum for each group avg current running sum for each group + current size of each group

  • Example: the maximum aggregate function

    initialize a search structure H on grouping attributes of γ; while ( R has more data blocks ) { read 1 data block in buffer b; for ( each tuple t ∈ b ) { /* ===================================================== We need a search structure H to implement the test t ∈ H efficiently !!! We can use hash table or some bin. search tree ====================================================== */ if ( t ∈ H ) { if ( value(t) > max( group(t) ) ) { max ( group(t) ) = value(t) ; } } else { insert t in H; max ( group(t) ) = value(t) ; } } } for ( each group ∈ H ) { Output group search key + max( group ); }

    ---

    ---

    ---

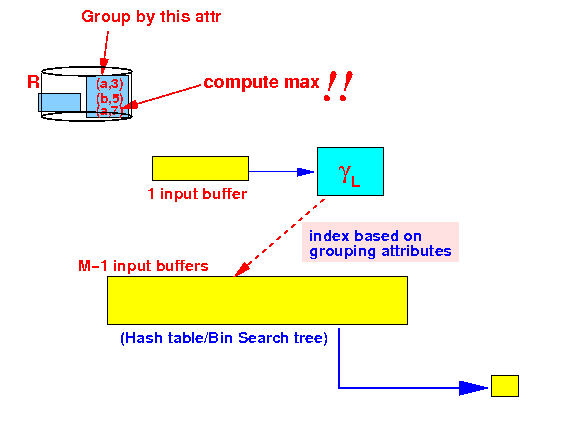
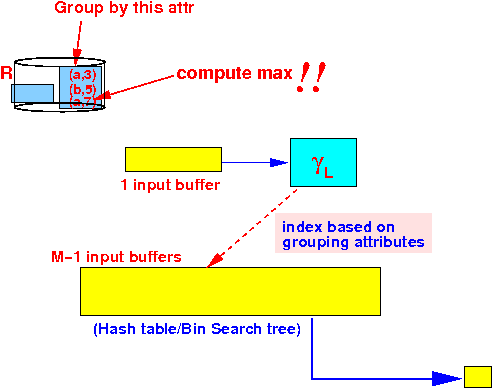
  • Example:

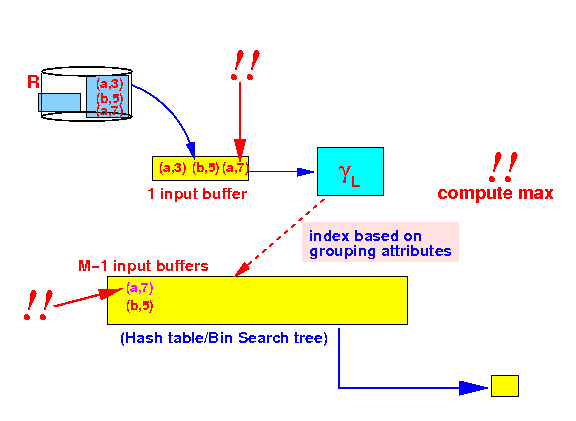
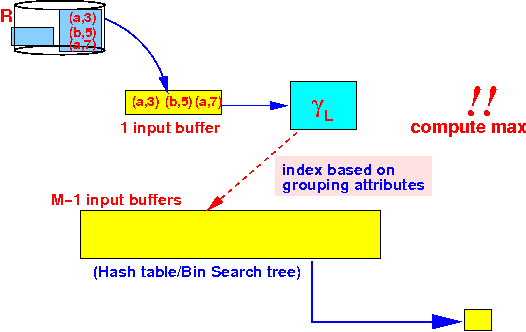
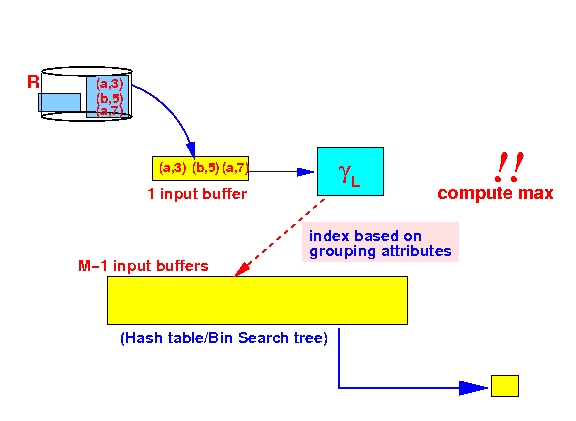
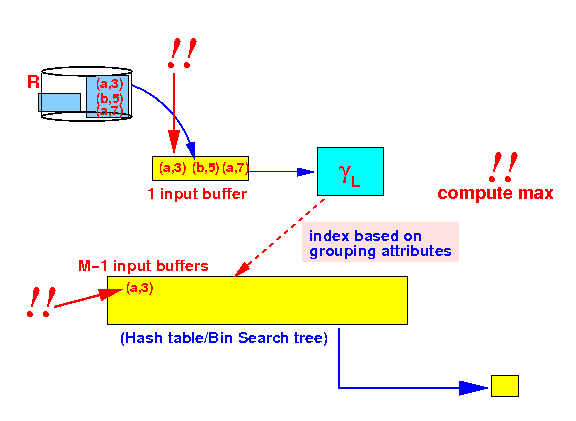
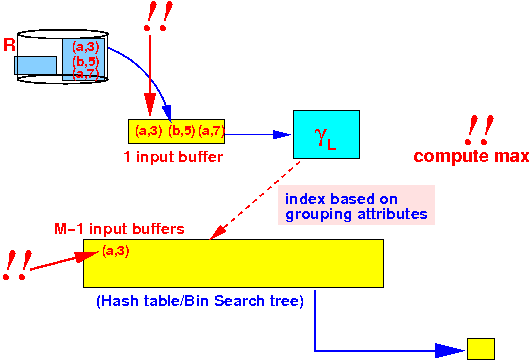
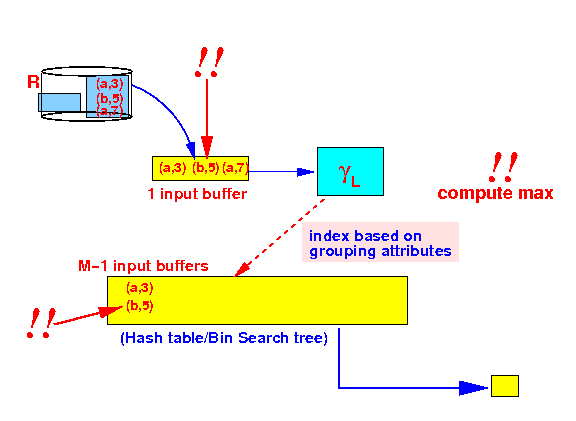
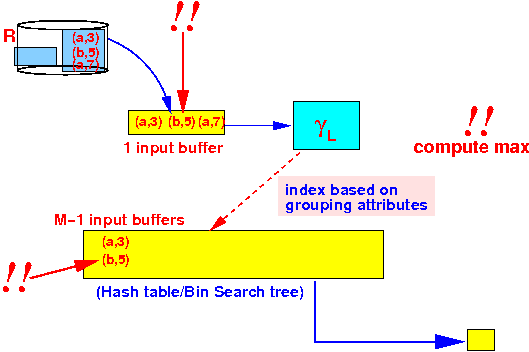
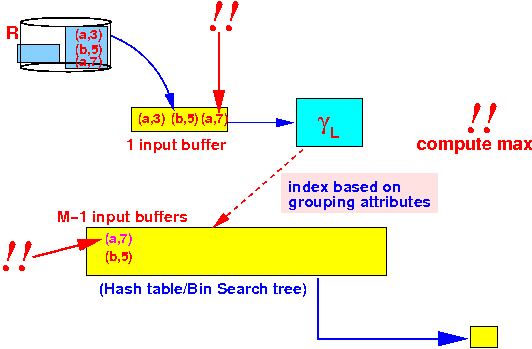
    Compute maximum of the 2nd attribute value on groups based on the first attribute: Read one block in: Process first tuple: Process 2nd tuple: Process 3rd tuple: Note: we update the current maximum value !!! And so on After all tuples are processed, then we output the statistics !!!

  ---

  ---

  ---

  ---

• Buffer utilization for γ_L (how to use buffers)

  • Buffer utilization when there are M buffers available:

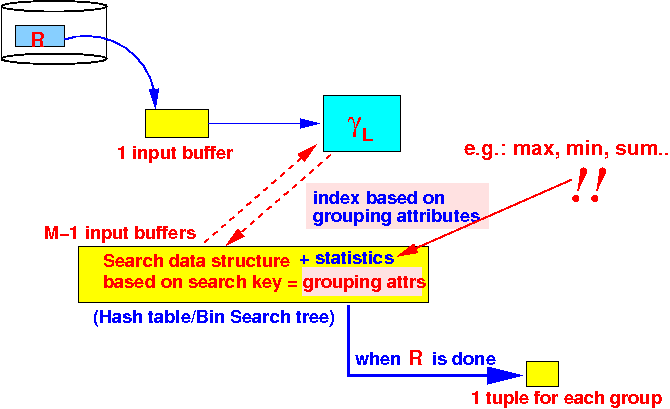
    Explanation:

    Use only one buffer to read in the tuples Use the remaning M−1 buffers to store the search structure (hash table)

  ---

  ---

  ---

  ---

• Cost Analysis (and constraint) for γ_L
  • # disk I/O used:

    B(R) --- if the relation R is clustered T(R) --- if the relation R is UNclustered

    ---

  • Memory requirement:

    M = O( V(R, [A1, A2, .., Ak]) )            where [A1, A2, .., Ak] are the grouping attributes V(R, [A1, A2, .., Ak]) × (size of k+1 attrs) M = --------------------------------------------- buffers block size

    Recall:

    V(R, [A1, A2, .., Ak]) = # distinct values that [A1, A2, .., Ak] can assume V(R, [A1, A2, .., Ak]) = | δ ( π A1, A2, .., Ak ( R ) ) |