Slideshow:
The bag difference
(−B) operator
Note: we need a search structure that contains (key, count (# occurences)) !
The bag difference
(−B) operator
- assumption
The bag difference
(−B) operator
- notable fact
Consequently: there are 2 algorithms for −B !!
The one-pass bag difference
S −B R
algorithm
S (smaller) −B R:
We must index the subtractor set
The one-pass bag difference
S −B R
algorithm
The one-pass bag difference
S −B R
algorithm
The one-pass bag difference
S −B R
algorithm
- Example
Phase 1: build search structure on S containing (key, count)
The one-pass bag difference
S −B R
algorithm
- Example
Phase 1: build search structure on S containing (key, count)
The one-pass bag difference
S −B R
algorithm
- Example
Phase 2: scan R and update count in search structure
The one-pass bag difference
S −B R
algorithm
- Example
Phase 2: scan R and update count in search structure - completed
The one-pass bag difference
S −B R
algorithm
- Example
Phase 2: after completion , we can output the bag difference
The one-pass bag difference
R −B S
algorithm
R −B S (smaller):
We must index the subtracted set
The one-pass bag difference
R −B S
algorithm
The one-pass bag difference
R −B S
algorithm
The one-pass bag difference
R −B S
algorithm
- Example
Phase 1: build search structure on S containing (key, count)
The one-pass bag difference
R −B S
algorithm
- Example
Phase 1: build search structure on S containing (key, count)
The one-pass bag difference
S −B R
algorithm
- Example
Phase 2: scan R and update count in search structure - if count = 0, output tuple
The one-pass bag difference
S −B R
algorithm
- Example
Phase 2: scan R and update count in search structure - if count > 0, decrement count
IO cost and buffer requirement for
−B
- Bag Difference operator:
R −B S - Example Bag Difference:
R = {1, 2, 2, 2, 3}; S = {2, 2, 3, 3, 4}; R −B S = { 1, 2 }
Assumption:
- The relation S is
the
smaller relation
- Building a search structure on S will minimize the memory requirement
- The relation S is
the
smaller relation
- There are actual
two difference operations:
1. S - R (S is the smaller of the 2 relations) 2. R - S (S is the smaller of the 2 relations)
- Example:
S = {2, 2, 3, 3, 4}; R = {1, 2, 2, 2, 3, 5}; {2, 2, 3, 3, 4} − {1, 2, 2, 2, 3, 5} = { 3, 4 } ^^^^^^^^^^^^^^ Index this set
- One-pass algorithm:
initialize a search structure H on all attributes ; /* ============================================================ Phase 1: Use 1 buffer and scan the SMALLER relation first. Build a search structure on the SMALLER relation The search structure contains a count for the search key ============================================================ */ while ( S has more data blocks ) { read 1 data block in buffer b; for ( each tuple t ∈ b ) { /* ===================================================== We need a search structure H to implement the test t ∈ H efficiently !!! We can use hash table or some bin. search tree ====================================================== */ if ( t ∉ H ) { insert t in H; initialize count(t) = 1 for H; } else { update count(t) = count(t) + 1 for H; } } } /* =================================================== Now we know how many of each element is in S =================================================== */ /* ============================================================ Phase 2: output tuples in S Use 1 buffer and scan the other relation. Use the search structure to remove common elements, but at most count times !! ============================================================ */ while ( R has more data blocks ) { read 1 data block in buffer b; for ( each tuple t ∈ b ) { /* ===================================================== We use search structure H to implement the test t ∈ H efficiently !!! We can use hash table or some bin. search tree ====================================================== */ if ( t ∈ H ) { if ( count(t) > 0 ) { Update count(t)-- in H; // We lost 1 copy of t } } else { // Ignore t, it's not in difference ! } } } /* =================================================== ONLY now we can output the difference =================================================== */ for ( every t ∈ H ) { output count(t) number of tuples t ; }
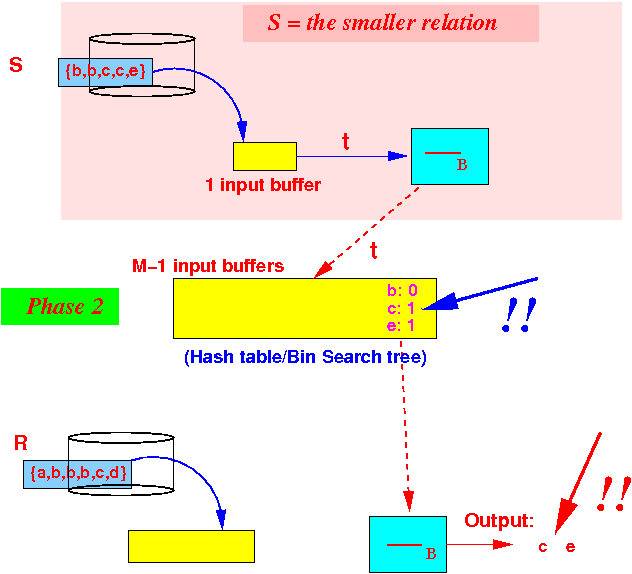
- Example:
compute:
S {b,b,c,c,e}
−B
R {a,b,b,b,c,d}
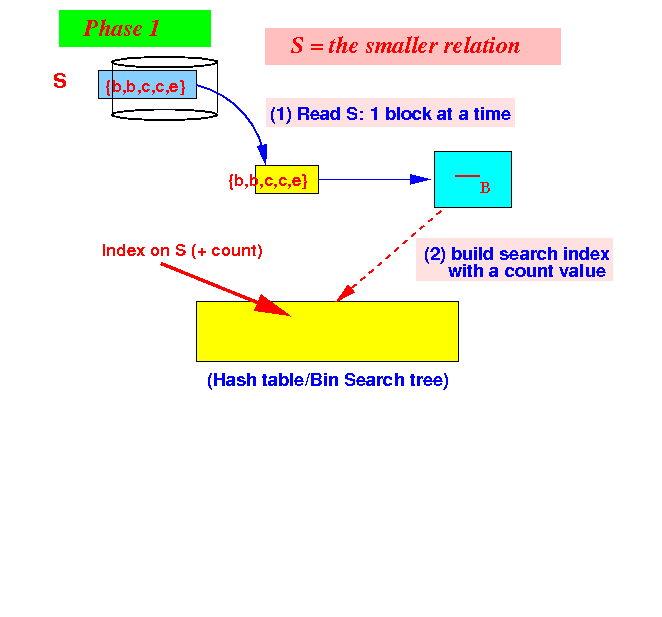
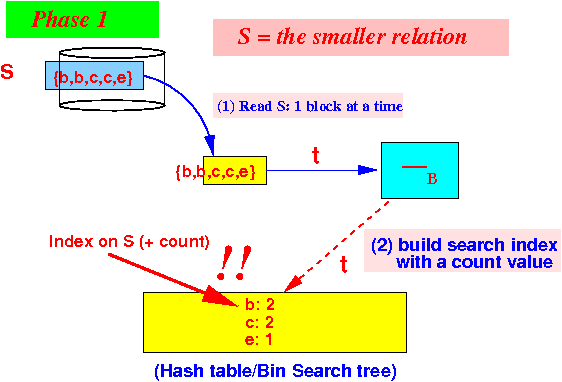
- Phase 1:
build index on
S
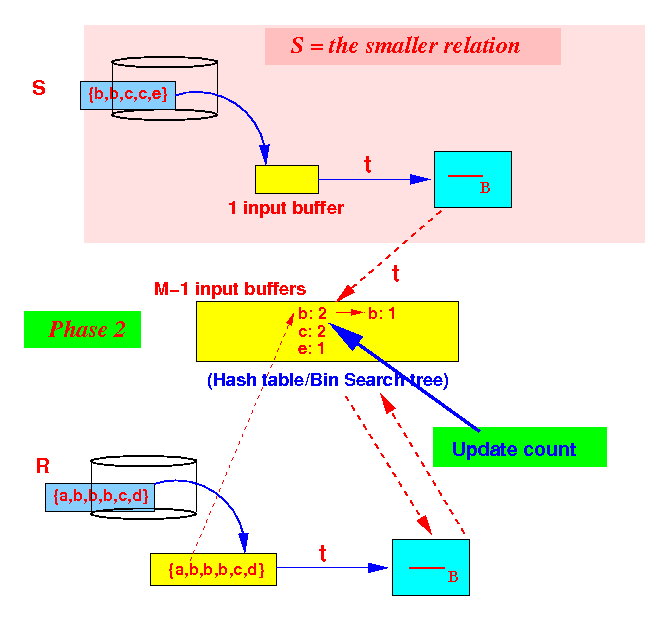
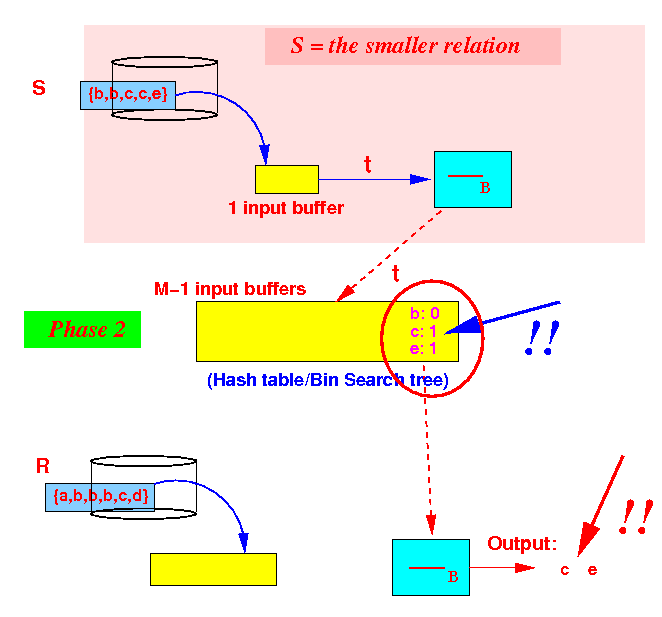
- Phase 2:
process
the tuples
in R
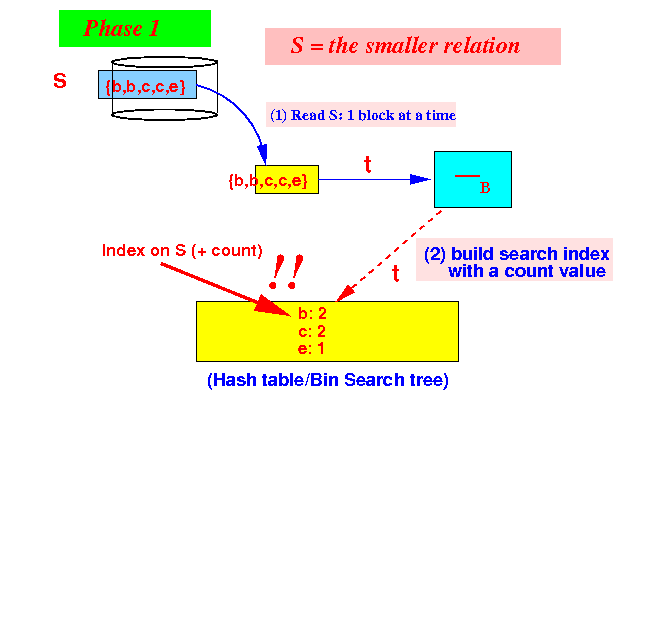
- Update the
count for
each tuple:
If tuple t is found, decrement the count by 1
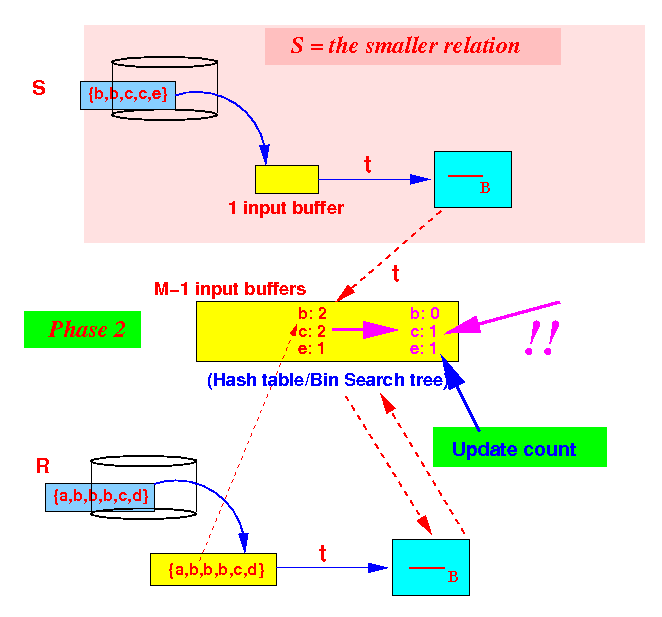
- Output the
remaining tuples
that has not been
subtracted away:
- Update the
count for
each tuple:
- Phase 1:
build index on
S
-
Buffer utilization when
there are M buffers
available:
- Phase 1:
partition the M buffers as
follows:
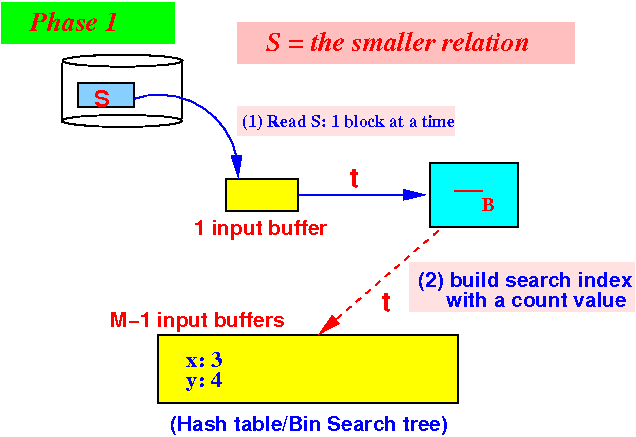
Use 1 buffer for input from S
Use M−1 buffers for the search structure with a count(t) for each unique element in S
- Phase 2:
partition the M buffers as
follows:
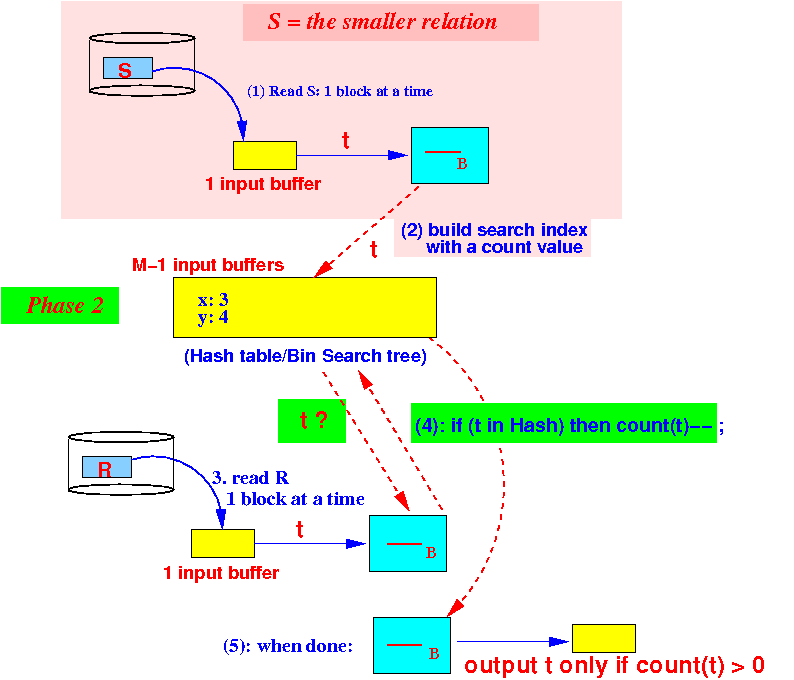
Use 1 buffer for input from R
We are still using M−1 buffers for the search structure in phase 2
- Phase 1:
partition the M buffers as
follows:
- Example:
R = {1, 2, 2, 2, 3, 5}; S = {2, 2, 3, 3, 4}; {1, 2, 2, 2, 3, 5} − {2, 2, 3, 3, 4} = { 1, 2, 5 } ^^^^^^^^^^^^^ Index this set
- One-pass algorithm:
initialize a search structure H on all attributes in tuples of S; /* ============================================================ Phase 1: (same) Use 1 buffer and scan the SMALLER relation first. Build a search structure on the SMALLER relation The search structure contains a count for the search key ============================================================ */ while ( S has more data blocks ) { read 1 data block in buffer b; for ( each tuple t ∈ b ) { /* ===================================================== We need a search structure H to implement the test t ∈ H efficiently !!! We can use hash table or some bin. search tree ====================================================== */ if ( t ∉ H ) { insert t in H; initialize count(t) = 1 for H; } else { update count(t) = count(t) + 1 for H; } } } /* =================================================== Now we know how many of each element is in S =================================================== */ /* ============================================================ Phase 2: output tuples in R Use 1 buffer and scan the other relation. Use the search structure to "throttle output" of common elements, but for at most count times !! ============================================================ */ while ( R has more data blocks ) { read 1 data block in buffer b; for ( each tuple t ∈ b ) { /* ===================================================== We use search structure H to implement the test t ∈ H efficiently !!! We can use hash table or some bin. search tree ====================================================== */ if ( t ∈ H ) { /* ============================================== Check if there is (still) a copy in S ============================================== */ if ( count(t) > 0 ) { Update count(t)-- in H; // We lost 1 copy of t } else { Output t; // Tuple did not get subtracted ! } else { Output t; // Tuple did not get subtracted ! } } }
- Example:
compute
R {a,b,b,b,c,d}
−B
S {b,b,c,c,e}
- Phase 1:
build index on
S
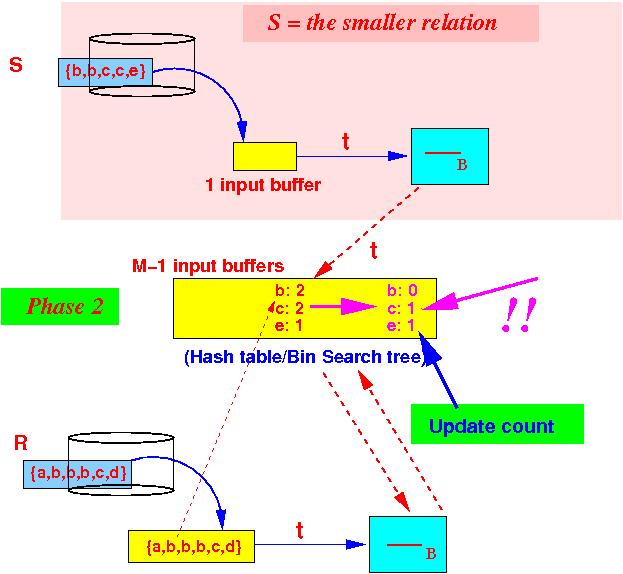
- Phase 2:
process
the tuples
in R
- If
count(x) == 0,
then:
output tuple x !
Example: tuple a
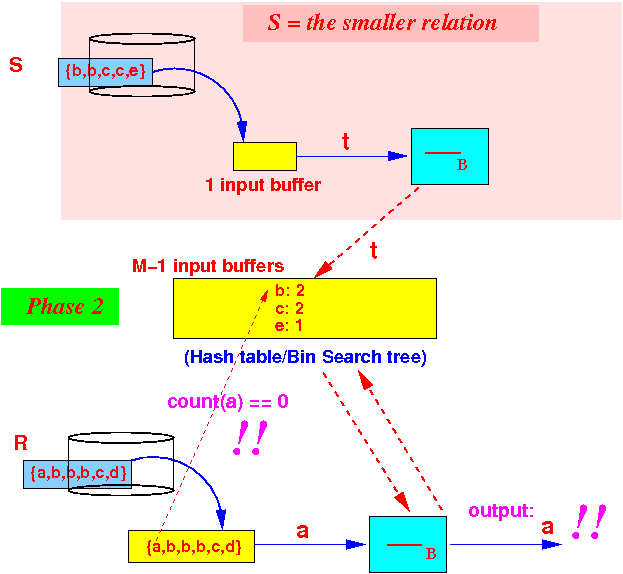
Tuple a is not found, so we output the tuple a
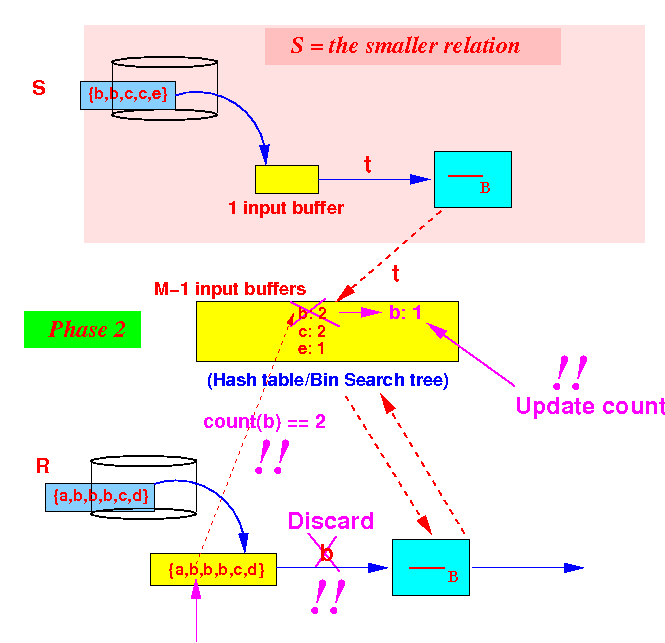
- Repeat --- if
count(x) == 0,
then:
output tuple x !
Example: tuple b
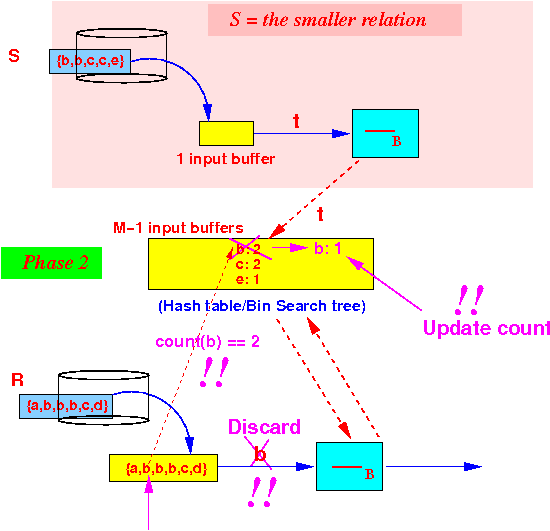
Count(b) = 1, so we discard the tuple b and descrement the count(b)
- And so on....
- If
count(x) == 0,
then:
output tuple x !
- Phase 1:
build index on
S
- Buffer utilization when
there are M buffers
available:
- Phase 1:
partition the M buffers as
follows:
Use 1 buffer for input from S
Use M−1 buffers for the search structure with a count(t) for each unique element in S
- Phase 2:
partition the M buffers as
follows:
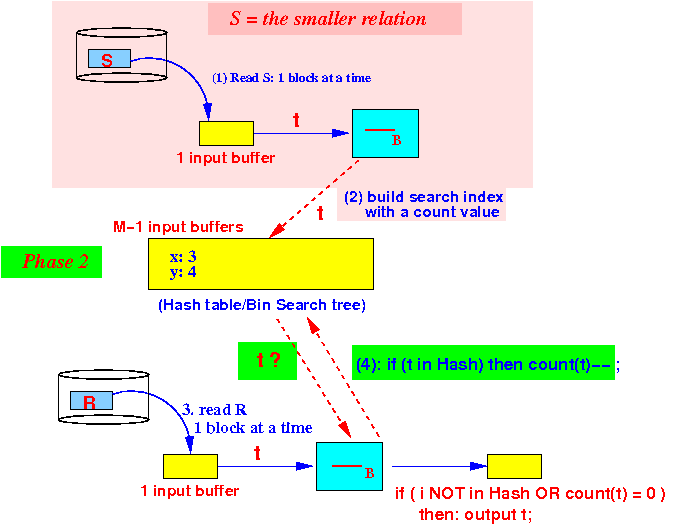
Use 1 buffer for input from R
We are still using M−1 buffers for the search structure in phase 2
- Phase 1:
partition the M buffers as
follows:
- # disk I/O used:
- B(R) + B(S) --- if the relations R and S are clustered
- Memory requirement:
- M ≥ B(S) + 1 buffer