Slideshow:
Prelude to the Nested-loop
Cartesian Product (×)
algorithm
The block-based
nested-loop Cartesian Product algorithm
The block-based
nested-loop Cartesian Product algorithm
- Example
Phase 1-1: read M−1 blocks from smaller relation S
The block-based
nested-loop Cartesian Product algorithm
- Example
Phase 2-1: use 1 buffer to scan relation R and combine with S's tuples in (M−1) buffers
The block-based
nested-loop Cartesian Product algorithm
- Example
Phase 1-2: read another M−1 blocks from smaller relation S
The block-based
nested-loop Cartesian Product algorithm
- Example
Phase 2-2: use 1 buffer to scan relation R and combine with S's tuples in (M−1) buffers
Important observation
We read M−1 blocks of relation S at a time.
For each chunk of S, we scan relation R once
# times R is scanned (read) = B(S)/(M−1)
Cost of the nested-loop Cartesian Product algorithm
Buffer requirement of the
nested-loop Cartesian Product algorithm
M ≥ 2 !!!
Interesting phenomenon: asymmetric cost
Interesting phenomenon: asymmetric cost
- Example
Interesting phenomenon: asymmetric cost
- Example
Interesting phenomenon: asymmetric cost
- Example
Interesting phenomenon: asymmetric cost
- Example
Interesting phenomenon: asymmetric cost
- Example
Interesting phenomenon: asymmetric cost
- Example
Interesting phenomenon: asymmetric cost
- Example
Interesting phenomenon: asymmetric cost
- Example
Interesting phenomenon: asymmetric cost
- Example
Previous result:
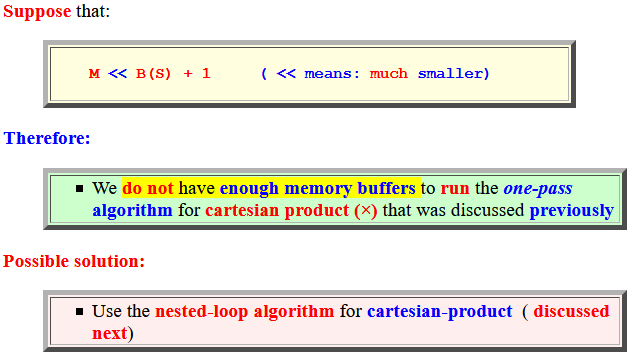
- Suppose that:
M << B(S) + 1 ( << means: much smaller)Therefore:
- We do not have enough memory buffers to run the one-pass algorithm for cartesian product (×) that was discussed previously
Possible solution:
- Use the nested-loop algorithm for cartesian-product ( discussed next)
- The block-based
nested-loop algorithm
to compute
the cartesian-product:
(is multiple runs of the one-pass cartesian product algorithm using (M−1) blocks of the S relation)
Let M = # available buffers; /* ------------------------------------------- Outer loop: read M-1 block of S ------------------------------------------- */ while ( S has more data blocks ) { read the next M-1 data blocks of S; // B(S) > M-1 !!! Rewind R; // Set read pointer back to the start of R /* ------------------------------------------- Innerloop: read through R and compute × ------------------------------------------- */ while ( R has more data blocks ) { read 1 data block of R; for ( each tuple s ∈ M-1 blocks of S and each tuple t ∈ 1 blocks of R ) do { output (s, t); } } }Graphically:
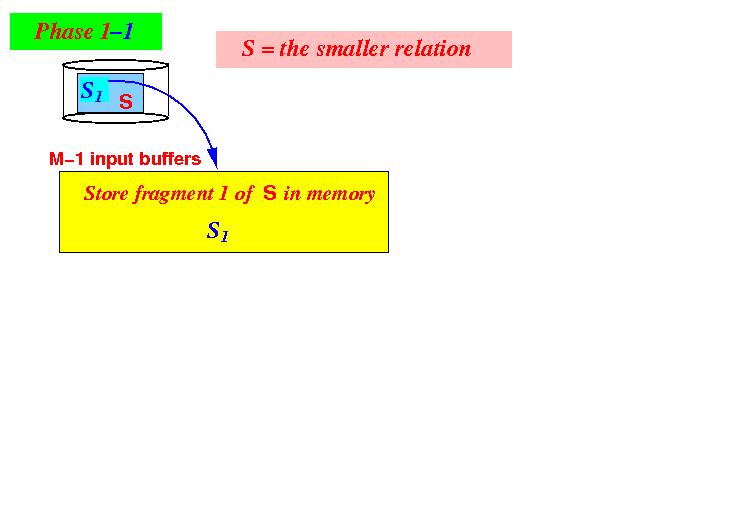
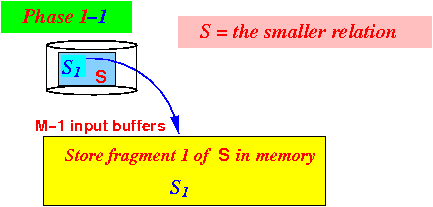
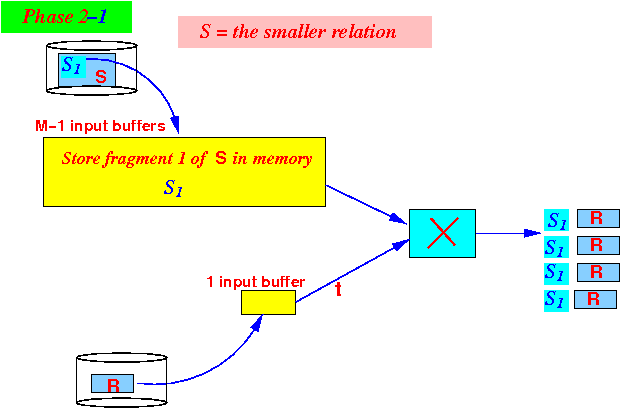
- Iteration 1:
- Use (M−1) blocks
to
read
the first fragment
S1 of
relation S
to memory:
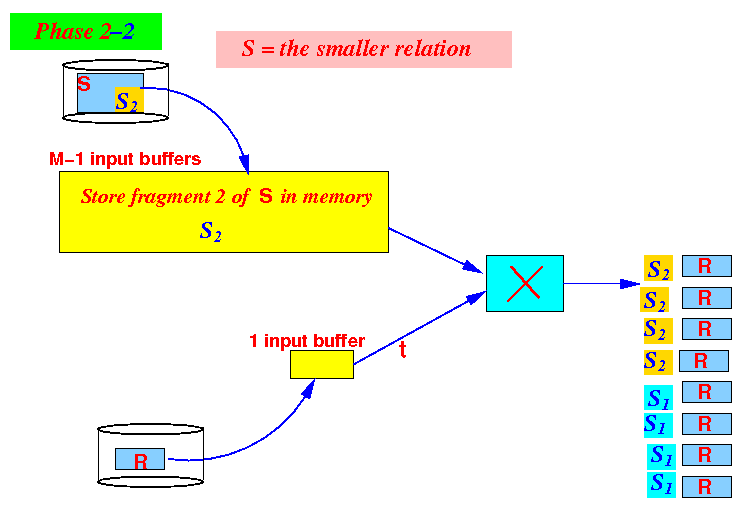
- Use
1 buffer to
read the
larger relation -
one block at a time -
and output
R ×
S1:
- Use (M−1) blocks
to
read
the first fragment
S1 of
relation S
to memory:
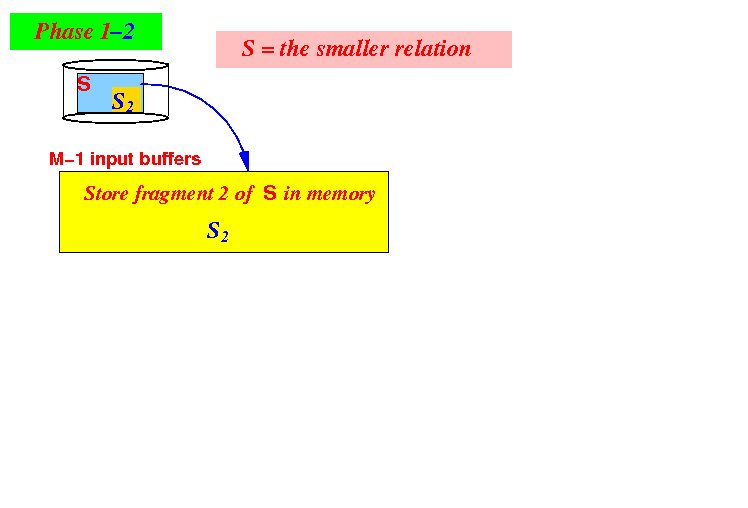
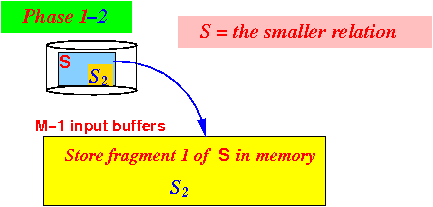
- Iteration 2:
- Use (M−1) blocks
to
read
the second fragment
S2 of
relation S
to memory:
- Use
1 buffer to
read the
larger relation -
one block at a time -
and output
R ×
S1:
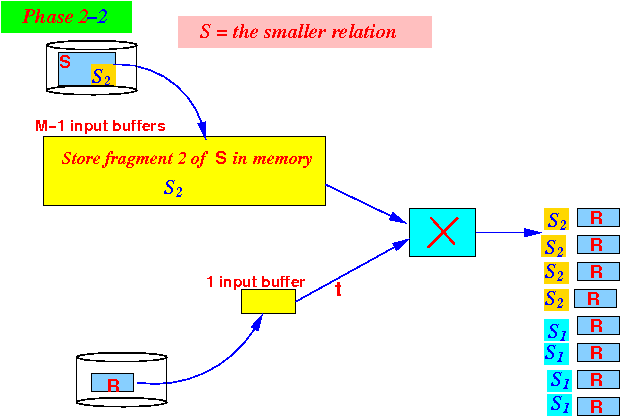
- Use (M−1) blocks
to
read
the second fragment
S2 of
relation S
to memory:
- And so on....
- Iteration 1:
-
Note:
- The nested-loop algorithm for
the cartesian product is
multi-pass algorithm:
- The nested-loop algorithm will
read
the relation S
once
- But: the nested-loop algorithm will read the relation R: B(S)/(M−1) times
- The nested-loop algorithm will
read
the relation S
once
- The nested-loop algorithm for
the cartesian product is
multi-pass algorithm:
- # disk I/O used:
Algorithm read S once: # disk I/Os = B(S)
# fragments of S read = B(S) / (M−1) For each fragment of S: Algorithm reads R once: # disk I/Os = B(S)/(M−1) × B(R)
So: B(S) Total cost = B(S) + ------- B(R) M-1
- Memory requirement:
- M ≥ 2 buffer
!!!!!
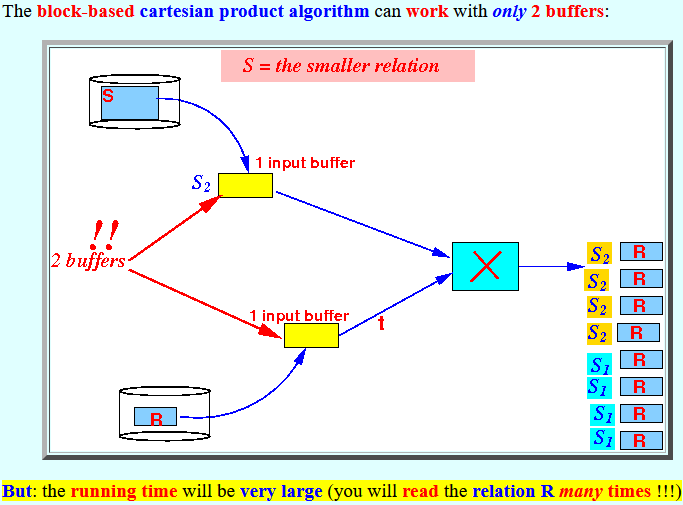
- The block-based
cartesian product algorithm can
work with
only
2 buffers:
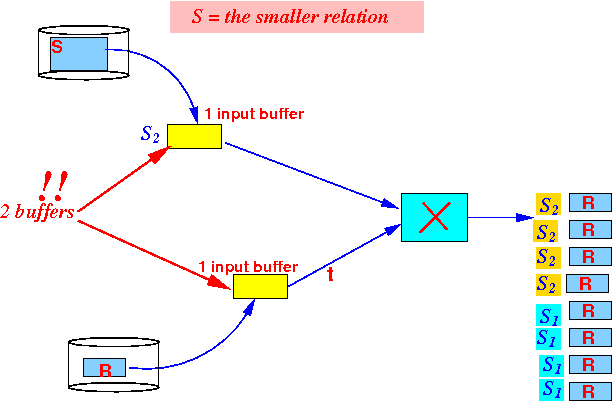
But: the running time will be very large (you will read the relation R many times !!!)
- The block-based
cartesian product algorithm can
work with
only
2 buffers:
- M ≥ 2 buffer
!!!!!
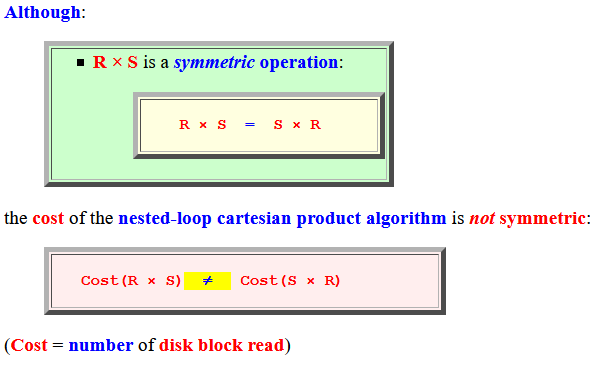
- Although:
- R × S is
a symmetric operation:
R × S = S × R
the cost of the nested-loop cartesian product algorithm is not symmetric:
Cost(R × S) ≠ Cost(S × R)(Cost = number of disk block read)
- R × S is
a symmetric operation:
- Example:
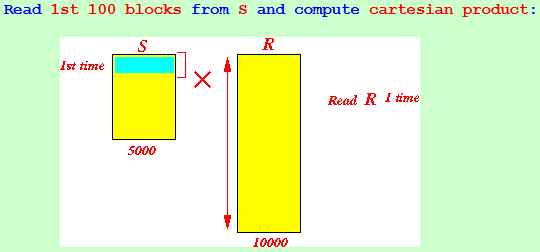
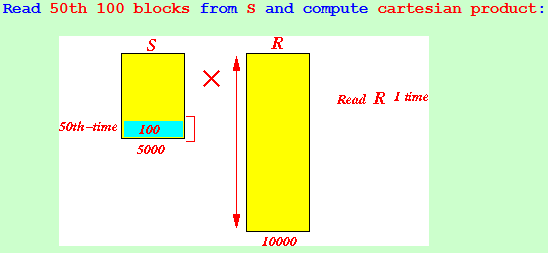
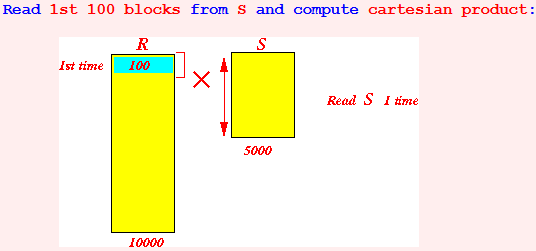
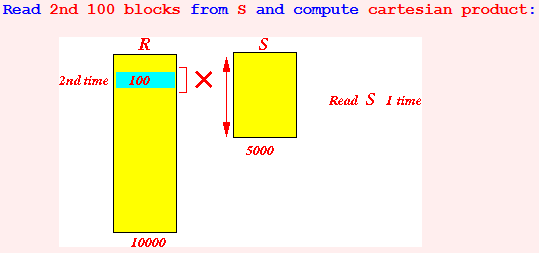
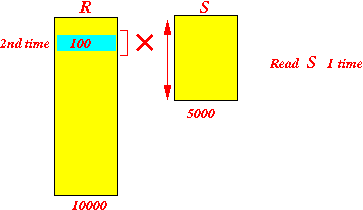
B(R) = 10,000 B(S) = 5,000 M = 101
- The cost to execute
the cartesian product
using
the smaller relation (S)
in the outer loop
is:
Configuration: (1) Use 100 buffers to hold tuples of S (2) Use 1 buffers to scan R
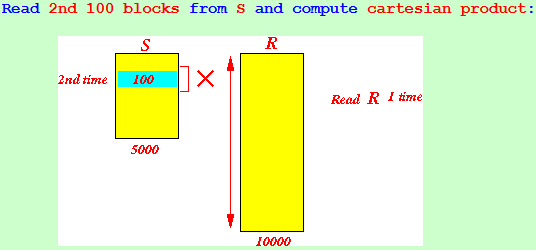
Read 1st 100 blocks from S and compute cartesian product: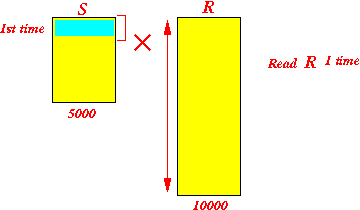
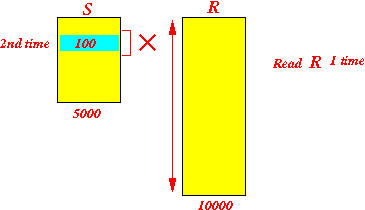Read 2nd 100 blocks from S and compute cartesian product:
...
Read 50th 100 blocks from S and compute cartesian product:
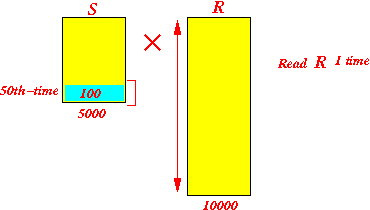
Total: B(S) + 50 × B(R) disk blocks = 5000 + 500000 = 505,000 blocks
- The cost to execute
the cartesian product
using
the larger relation (R)
in the outer loop is:
Configuration: (1) Use 100 buffers to hold tuples of R (2) Use 1 buffers to scan S
Read 1st 100 blocks from S and compute cartesian product: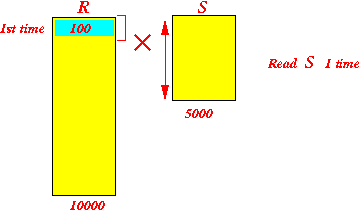
Read 2nd 100 blocks from S and compute cartesian product:
...
Read 100th 100 blocks from S and compute cartesian product:
Total: B(R) + 100 × B(S) disk blocks = 10000 + 500000 = 510,000 blocks