Slideshow:
- The zig-zag join
algorithm using a
clustering index
is
the same algorithm
as for
a non-clustering index:
The zig-zag join algorithm using a clustering index:
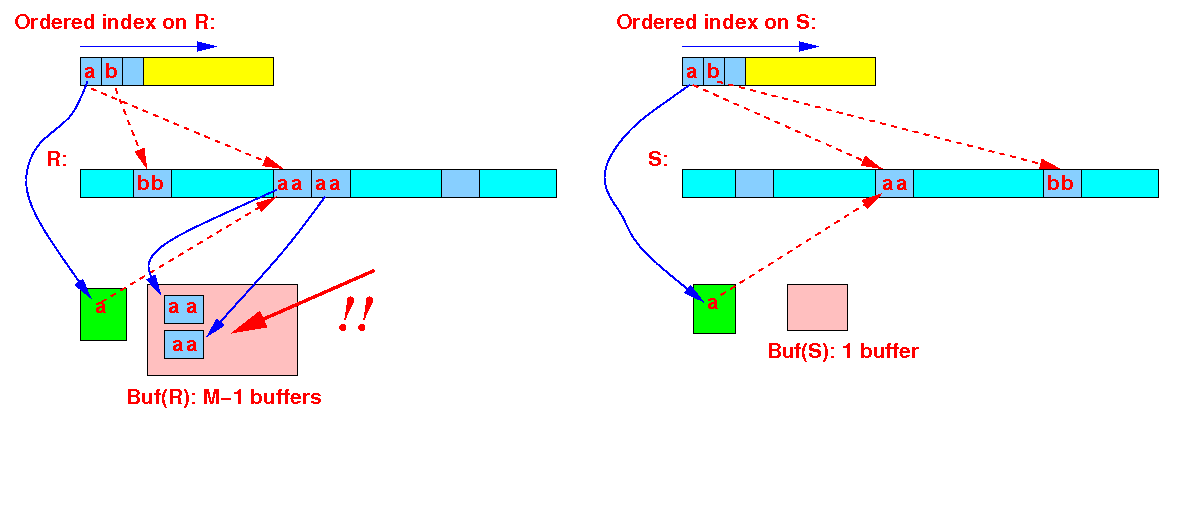
while ( R ≠ empty and S ≠ empty ) do { Read the index entries of R with the smallest key r :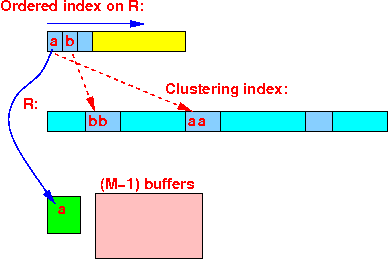 Read the index entries of S with the smallest key s :
Read the index entries of S with the smallest key s :
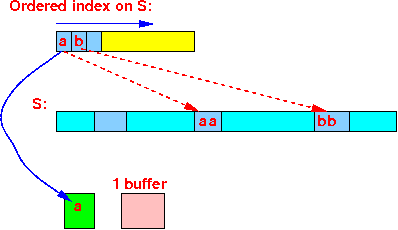 if ( search key r < search key s )
{
discard all search keys r;
(and repeat...)
}
else if ( search key s < search key r )
{
discard all search keys s;
(and repeat....)
}
if ( search key s = search key r )
{
Read in all tuples of R with smallest search key (r) into M-1 buffers:
if ( search key r < search key s )
{
discard all search keys r;
(and repeat...)
}
else if ( search key s < search key r )
{
discard all search keys s;
(and repeat....)
}
if ( search key s = search key r )
{
Read in all tuples of R with smallest search key (r) into M-1 buffers:
 Use 1 buffer to read in all tuples of S with same join value;
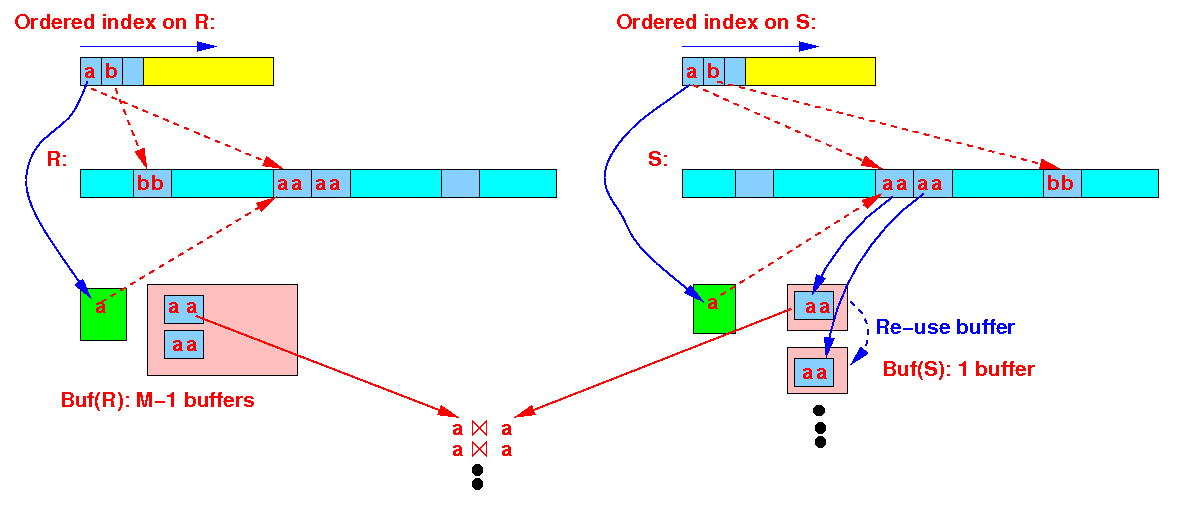
Join the tuples in Buf(R) and Buf(S):
Use 1 buffer to read in all tuples of S with same join value;
Join the tuples in Buf(R) and Buf(S):
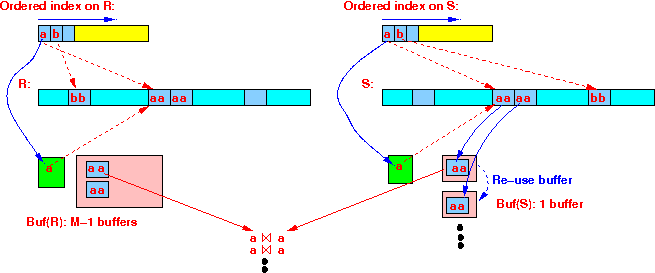 Join all tuples in Buf(R) and Buf(S);
Join all tuples in Buf(R) and Buf(S);
 After joining: discard search keys r and s in Buf(R) and Buf(S);
(Repeat....)
}
}
After joining: discard search keys r and s in Buf(R) and Buf(S);
(Repeat....)
}
}
- The difference between
clustering and
non-clustering index is
the access pattern to
the data file (tuples):
- Using a clustering index,
we will read all joining
tuples
in
consecutive blocks :
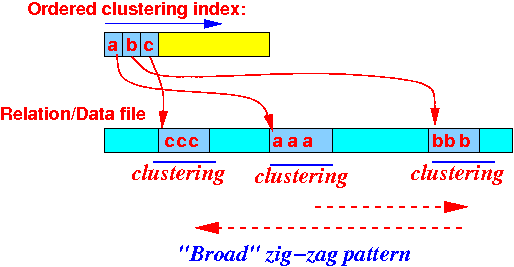
- Using a clustering index,
we will read all joining
tuples
in
consecutive blocks :
- # disk accesses
to join R ⋈ S
using
a clustering index:
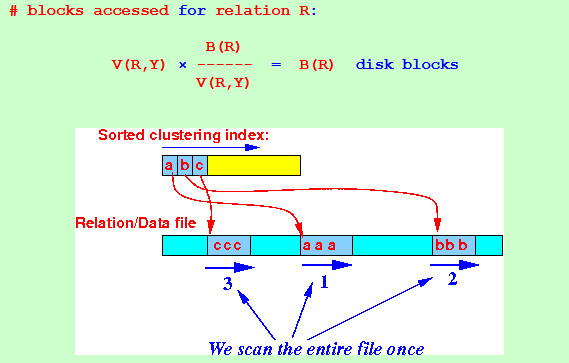
For relation R: 1. Read the ordered clustering index file Index files are relatively small So: we will ignore this cost 2. For each search key value: (index is clustering) B(R) read ------- data block to access the joining tuples V(R,Y) 3. # different search key values = V(R,Y) # blocks accessed for relation R: B(R) V(R,Y) × ------ = B(R) disk blocks V(R,Y)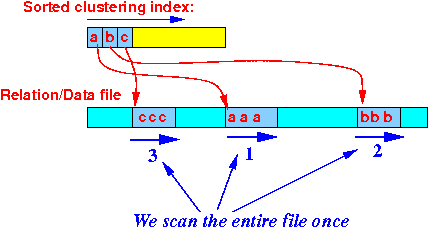
For relation S: 1. Read the ordered clustering index file Index files are relatively small So: we will ignore this cost 2. For each search key value: (index is clustering) B(S) read ------- data block to access the joining tuples V(S,Y) 3. # different search key values = V(S,Y) # blocks accessed for relation R: B(S) V(S,Y) × ------ = B(S) disk blocks V(S,Y)
Total # blocks accessed ~= B(R) + B(S)