---

Processing R ⋈ S using a clustering index

---

---

---

 

Slideshow:

The index-join algorithm

Pseudo code:
while ( R ≠ EOF ) { read next block of R in buffer b; for ( each tuple t ∈ b ) do { (1) Use t(Y) to lookup in index Y of relation S; (2a) access all tuples s with s(Y)=t(Y); (2b) output t ⋈ s } }
Note: the index can be an ordered index or a hash index !!!
The performance of the index-join algorithm using a clustering index
What is the IO cost to Compute R ⋈ S when:
 
The performance of the index-join algorithm using a clustering index
What is the IO cost to Compute R ⋈ S when:
 
The join algorithm will scan the relation R once:
   
IO cost so far:   B(R)           (or:   T(R) if R is not clustered)
The performance of the index-join algorithm using a clustering index
What is the IO cost to Compute R ⋈ S when:
 
For each tuple t ∈ R, we read B(S)/V(S,Y) blocks of relation S (and join (⋈) with tuple t):
   
IO cost so far:   B(R) + T(S) × B(S)/V(S,Y)
The performance of the index-join algorithm using a clustering index
 
 

(The cost to scan relation R depends on whether R is clustered or unclustered)
❮ ❯



---

---

---

---

• Prelude....
  • Note:

    ⋈ is the natural join operator This material is valid for any join operation using = as join condition

  ---

  ---

  ---

  ---

• Processing R ⋈ S using a clustering index
  • Requirement:

    R = (X, Y) S = (Y, Z) S has an clustering index on Y

    Index join:

    We use σA=c(S) to process the join operation where c = attribute value in a tuple ∈ R

    ---

    ---

  • Algorithm for R ⋈ S using index S.Y:

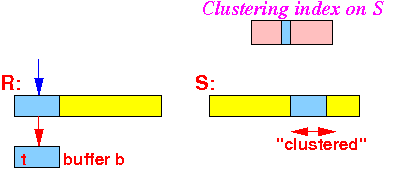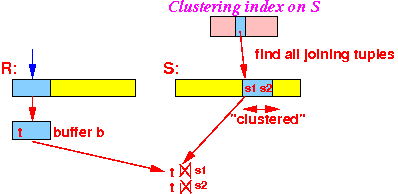
    while ( R ≠ EOF ) { read next block of R in buffer b; for ( each tuple t ∈ b ) do { (1) Use t(Y) to lookup in index Y of relation S: 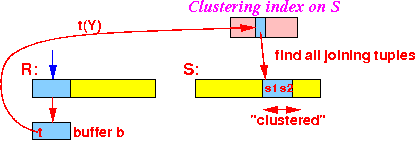(2a) read all tuples s with s(Y)=t(Y); (2b) output t ⋈ s: } } }

  ---

  ---

  ---

  ---

• Performance analysis of the Join algorithm for a clustering index
  • The join algorithm will scan the relation R once:

    ---

    ---

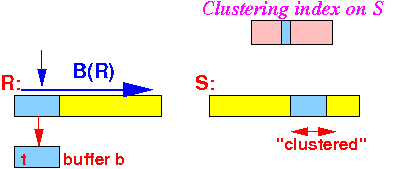
  • For each tuple t ∈ R, we read B(S)/V(S,Y) blocks of relation S to perform the join (⋈) operation with tuple t:

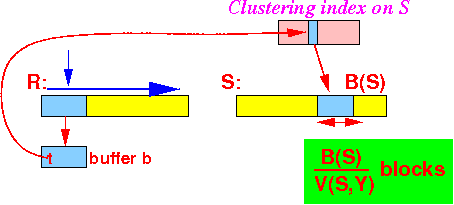
    Reason: the index is clustering:

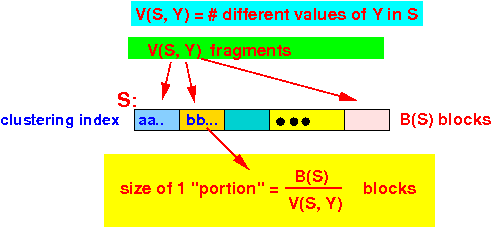
    We do this for T(R) tuples in relation R.

    ---

    ---

    ---

    ---

  • Therefore:    # disk IO used in join algorithm with an clustering index:

    # disk IOs = Scan R (once) + # tuples in R × # blocks of S read per tuple of R If relation R is clustered: B(S) = B(R) + T(R) × -------- // Scan cost for clustered file R = B(R) V(S,Y) If relation R is non-clustered: B(S) = T(R) + T(R) × -------- // Scan cost for non-clustered file R = T(R) V(S,Y)