Slideshow:
The join (⋈) operator
(Cannot build a search structure because there is not enough memory)
The IO-intensive
TPMMS base join (⋈) algorithm
- Pass 1
(Graphically explained in next slide)
The IO-intensive
TPMMS base join (⋈) algorithm
- Pass 1
Run the complete TPMMS sort algorithm on R and S (separately):
Result: R and S are sorted and stored on disk
The IO-intensive
TPMMS base join (⋈) algorithm
- Pass 2
The IO-intensive
TPMMS base join (⋈) algorithm
- Pass 2
Use this procedure to join the tuples of R (with value X) by scanning S:
(Graphically explained in next slide)
The IO-intensive
TPMMS base join (⋈) algorithm
- Pass 2
Store all tuples with the same join value in R and use use 1 buffer to scan S:
IO cost of
the IO-intensive
TPMMS base join (⋈) algorithm
Remark: this is a 3-pass algorithm !
Memory requirement of
the IO-intensive
TPMMS base join (⋈) algorithm
Memory constraint 1:
Memory requirement of
the IO-intensive
TPMMS base join (⋈) algorithm
Memory constraint 2:
Memory requirement of
the IO-intensive
TPMMS base join (⋈) algorithm
Memory constraint summary:
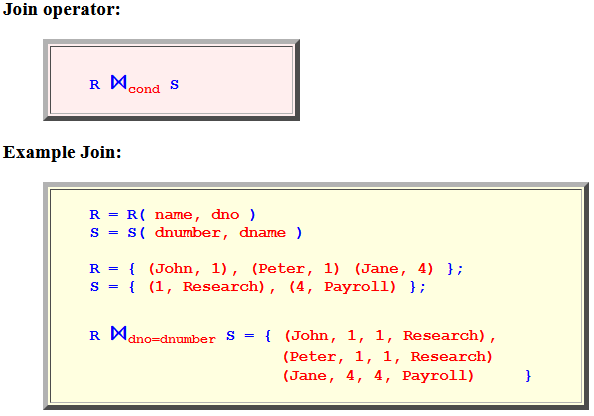
- Join operator:
R ⋈cond S - Example Join:
R = R( name, dno ) S = S( dnumber, dname ) R = { (john, 1), (jane, 4) }; S = { (1, Research), (4, Payroll) }; R ⋈dno=dnumber S = { (john, 1, 1, Research), (jane, 4, 4, Payroll) }
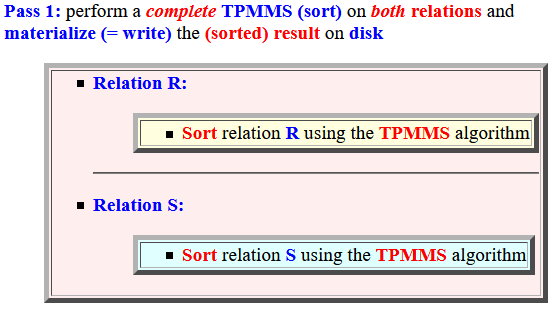
- Pass 1: perform a
complete
TPMMS (sort) on
both relations
and materialize (= write) the
(sorted) result
on disk
- Relation R:
- Sort relation R using the TPMMS algorithm
- Relation S:
- Sort relation S using the TPMMS algorithm
Graphically: (this is the TPMMS algorithm)
- Relation R:
- Pass 2:
join
the sorted relations:
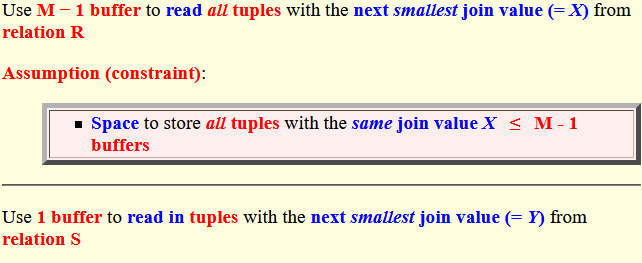
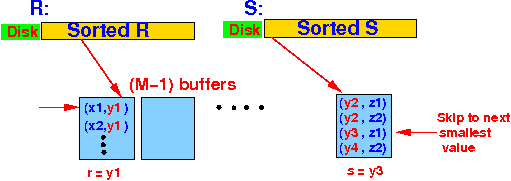
- Use M − 1 buffer to
read
all tuples with
the next smallest join value
(= X)
from relation R
Assumption (constraint):
- Space to store all tuples with the same join value X ≤ M - 1 buffers
- Use 1 buffer to
read in
tuples
with
the next smallest join value
(= Y)
from relation S
Perform the join using the following algorithm:
- If Y < X:
- Use the next
smallest join value
in relation S
(advance tuples in relation S to try reach the join value Y)
- Use the next
smallest join value
in relation S
- If X < Y:
- Use the next
smallest join value
in relation R
(Read all tuples with the next smallest join value into the M−1 buffers)
- Use the next
smallest join value
in relation R
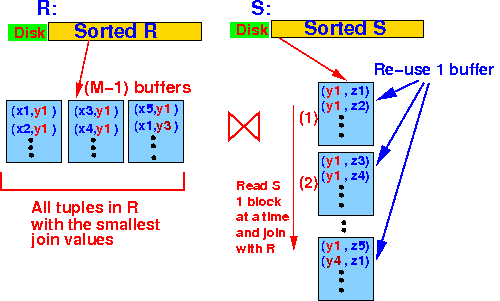
- If Y = X:
- Join the
tuples with
join value Y=X
of relation S in
the (one) buffer
with all tuples
from relation R
- If all tuples in
the (one) buffer of S are
used in
join:
- Read next buffer from S and repeat
- Join the
tuples with
join value Y=X
of relation S in
the (one) buffer
with all tuples
from relation R
- If Y < X:
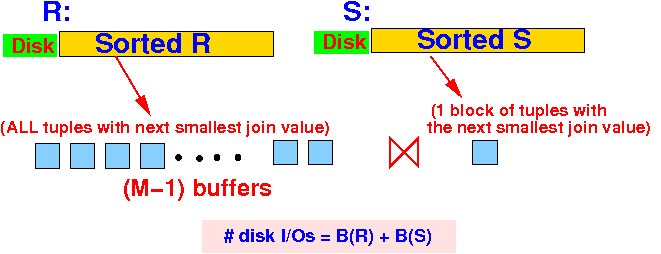
The sort-join Algorithm:
Read R until all tuples with 1st join value are stored in memory buffers; Read the first block of S; While ( R ≠ empty OR S ≠ empty ) { Let r = the current smallest join value ∈ R Let S = the current smallest join value ∈ S if ( r < s ) { Situation: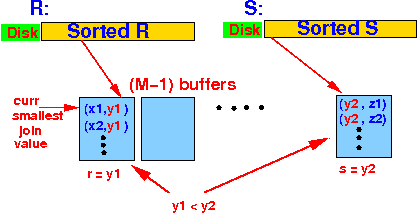
skip all tuples with join attr y1 in R;
}
else if ( s < r )
{
skip all tuples with join attr y1 in S;
}
else /* r = s = y1 */
{ /* ===================================================
Join on join value r = s = y1
=================================================== */
read S as long as join attr = s (= y1);
Join tuples in S with join attr = y1;
When done:
reuse buffers;
Read R until all tuples with next smallest join value
are stored in memory buffers;
}
}
- Use M − 1 buffer to
read
all tuples with
the next smallest join value
(= X)
from relation R
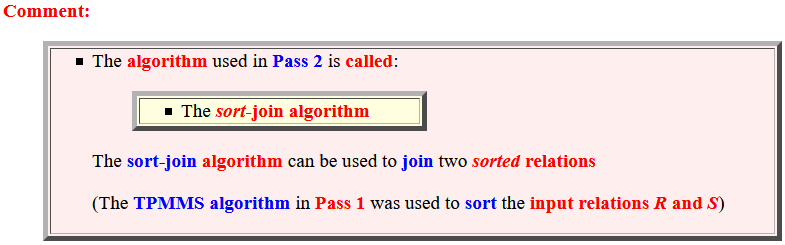
- Comment:
- The algorithm used in
Pass 2 is
called:
- The sort-join algorithm
The sort-join algorithm can be used to join two sorted relations
(The TPMMS algorithm in Pass 1 was used to sort the input relations R and S)
- The algorithm used in
Pass 2 is
called:
- # disk I/O used: (assume that
R is
clustered)
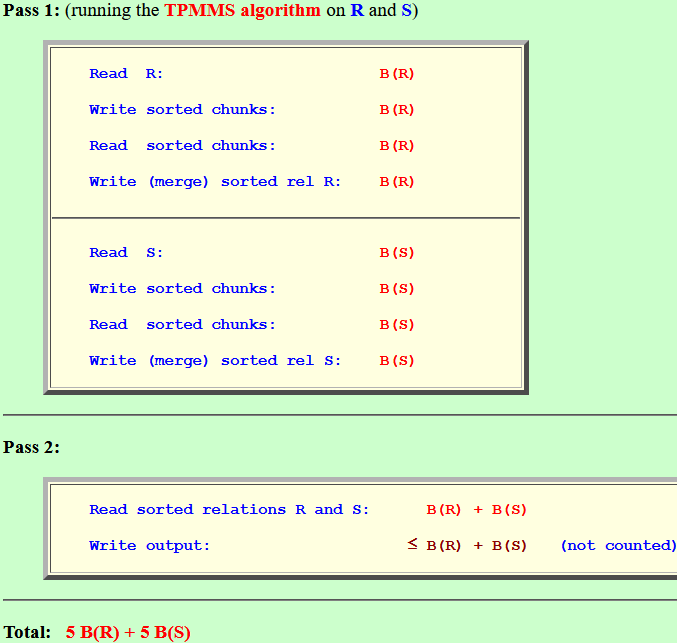
- Pass 1: (running the
TPMMS algorithm on
R and S)
Read R: B(R) Write sorted chunks: B(R) Read sorted chunks: B(R) Write (merge) sorted rel R: B(R)
Read S: B(S) Write sorted chunks: B(S) Read sorted chunks: B(S) Write (merge) sorted rel S: B(S)
- Pass 2:
Read sorted relations R and S: B(R) + B(S) Write output: ≤ B(R) + B(S) (not counted)
- Total: 5 B(R) + 5 B(S)
- Pass 1: (running the
TPMMS algorithm on
R and S)
- Comment:
- Technically, the
IO-intensive join algorithm
is a three-pass algorithm:
- In Pass 1, the
IO-intensive join algorithm read
relation R and S:
2 times !!!
- In Pass 2, the IO-intensive join algorithm read relation R and S: 1 time
- In Pass 1, the
IO-intensive join algorithm read
relation R and S:
2 times !!!
- Technically, the
IO-intensive join algorithm
is a three-pass algorithm:
- Recall the
steps:
- We used TPMMS
sort
R
and S individually
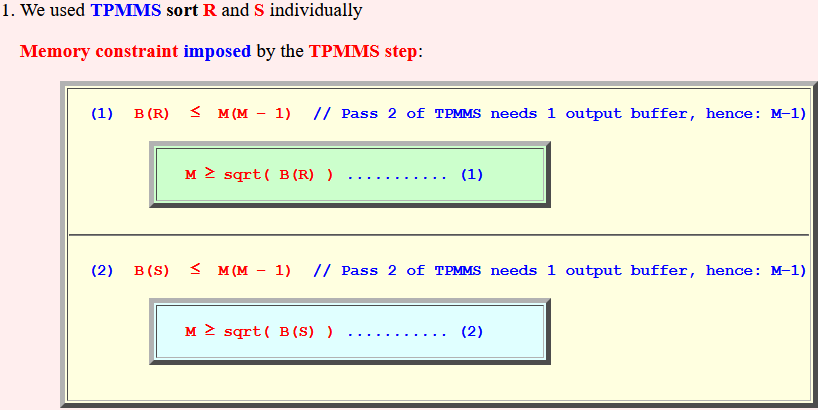
Memory constraint imposed by the TPMMS step:
(1) B(R) ≤ M(M − 1) // Pass 2 of TPMMS needs 1 output buffer, hence: M−1)
M ≥ sqrt( B(R) ) ........... (1)
(2) B(S) ≤ M(M − 1) // Pass 2 of TPMMS needs 1 output buffer, hence: M−1)M ≥ sqrt( B(S) ) ........... (2)
- Furthermore,
we can use at most
(M−1) bufferss
to hold
joining tuples from
R:
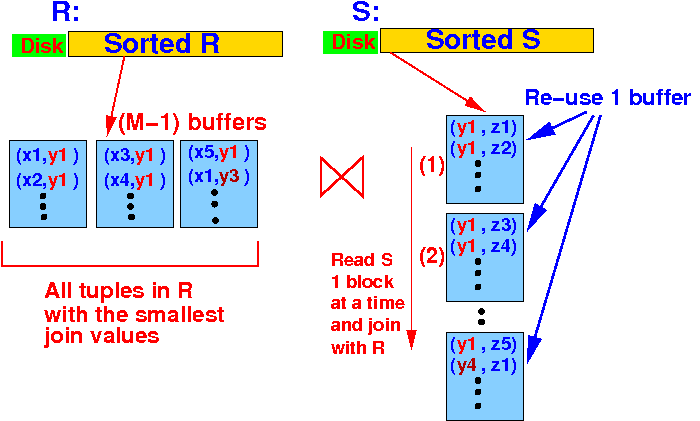
Therefore:
- Size of the tuples in R with same join attribute value ≤ (M−1) blocks
- We used TPMMS
sort
R
and S individually
- The memory constraints are:
(1) In order to sort the relation R using TPMMS: -------- M ≥ \/ B(R) buffers // From: B(R) ≤ M(M − 1)
(2) In order to sort the relation S using TPMMS: -------- M ≥ \/ B(S) buffers // From: B(S) ≤ M(M − 1)
(3) Join tuples with equal join attr values: Size of tuples in R with common join attr. values ≤ (M-1) blocks
- Recall:
Cost Anslysis
of the Nested-Loop Join Algorithm
(1) Nested-loop will read S once: # disk I/Os = B(S) (2) Number of fragments Si read by Nested-loop: B(S)/(M-1) Nested-loop will read R: B(S)/(M-1) times # disk I/Os = (B(S)/(M-1)) × B(R)
B(S) Total cost = B(S) + ------- B(R) M-1 B(S)×B(R) t = B(S) + -------- M-1So:
# Disk IO (nested-loop join) = O ( B(R) × B(S) )
- The IO intensive version of
the TPMMS-base join algorithm:
# Disk IO (TPMMS-based join) = 5 B(R) + 5 B(S) = O( B(R) + B(S) )
- Conclusion:
- The TPMMS-base join algorithm is
preferred over
the nested-loop join
(if memory constraints allows it !!!)
- The TPMMS-base join algorithm is
preferred over
the nested-loop join