Slideshow:
The grouping operator (γ)
The 2-pass TPMMS based grouping
(γ) algorithm
- Pass 1
The 2-pass TPMMS based grouping
(γ) algorithm
- Pass 2
Pass 2:
(I.e.: you can process all tuples in the "smallest" group first - graphically explained in next slide)
The 2-pass TPMMS based grouping
(γ) algorithm
- Pass 2
Pass 2:
You only need a program variable to store 1 tuple for the output (i.e.: not an entire buffer)
The 2-pass TPMMS based grouping
(γ) algorithm
- Example
- Pass 1
Input file:
The 2-pass TPMMS based grouping
(γ) algorithm
- Example
- Pass 1
Pass 1: read chunks of M blocks and sort on the grouping attributes
Write the sorted chunks to disk
The 2-pass TPMMS based grouping
(γ) algorithm
- Example
- Pass 2
Pass 2: read 1 block from every (sorted) chunk and find the next smallest tuple (= group)
If smallest tuple ≠ last seen tuple then initialize the statistic for this (new) group
The 2-pass TPMMS based grouping
(γ) algorithm
- Example
- Pass 2
Pass 2: read 1 block from every (sorted) chunk and find the next smallest value
If smallest tuple = last seen tuple then update the statistic of this group
Cost analysis of
the 2-pass TPMMS based grouping
(γ) algorithm
Buffer requirement of
the 2-pass TPMMS based grouping
(γ) algorithm
The relation R can be sorted into at most M chunks, because in Pass 2, we can use at most M buffers:
(We need to use 1 buffer to read 1 sorted chunk)
Buffer requirement of
the 2-pass TPMMS based grouping
(γ) algorithm
I.e.: if the size of relation R is B(R) blocks, we need M = Sqrt(B(R)) buffers to execute 2-pass TPMMS based γ algorithm
- Grouping operator:
γL ( R )Note: L can be one of the following functions:
- min (find the minimum value in each group
- max (find the maximum value in each group
- count (find the cardinality (# members) in each group
- sum (find the sum (of some attribute value) in each group
- avg (find the average (of some attribute value) in each group
- Example Grouping:
R = (x,y) R = { (a,2), (a,3), (b,1), (b,3) } γavg(y) ( R ) = { (a, 2.5), (b, 2) }
- Pass 1:
(similar as
TPMMS ---
use grouping attributes
as sort key)
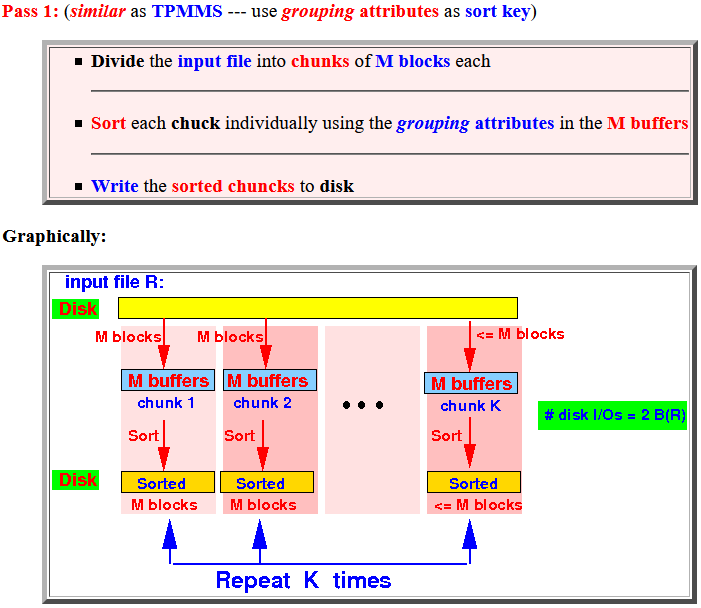
- Divide the
input file into
chunks of
M blocks each
- Sort each chuck
individually using the
grouping attributes
in the
M buffers
- Write the sorted chuncks to disk
Graphically:
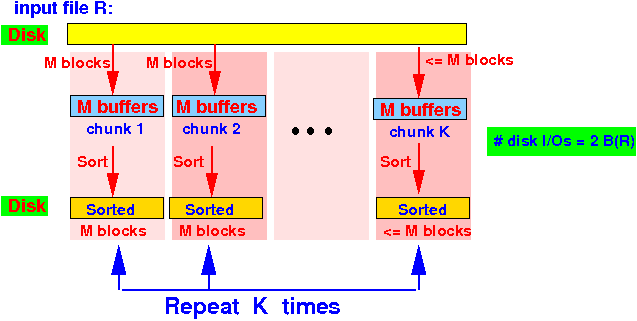
- Divide the
input file into
chunks of
M blocks each
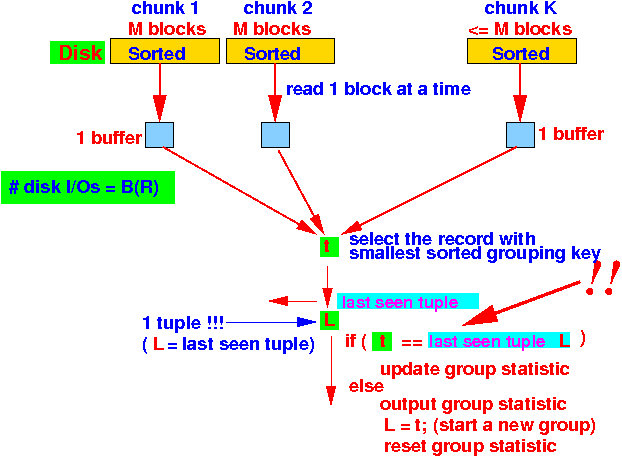
- Pass 2:
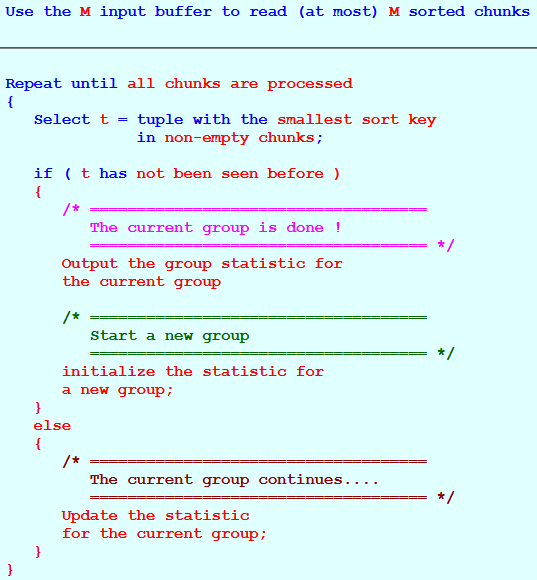
Use the M input buffer to read (at most) M sorted chunks
Repeat until all chunks are processed { Select t = tuple with the smallest sort key in non-empty chunks; if ( t has not been seen before ) { /* ==================================== The current group is done ! ==================================== */ Output the group statistic for the current group /* ==================================== Start a new group ==================================== */ initialize the statistic for a new group; } else { /* ==================================== The current group continues.... ==================================== */ Update the statistic for the current group; } }Graphically:
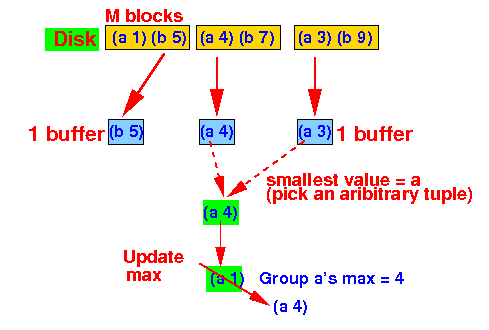
- Example:
compute maximum
of the 2nd attribute value
(groups formed
using the first attribute value)
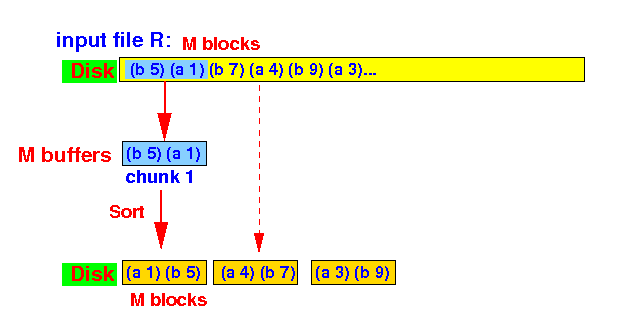
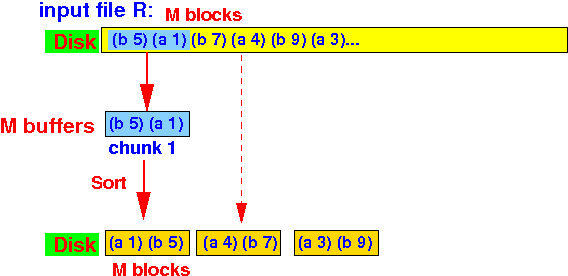
- Input:
- Pass 1:
sort
input relation into
chunks of
M blocks
- Pass 2:
compute the
(set) function on
each group:
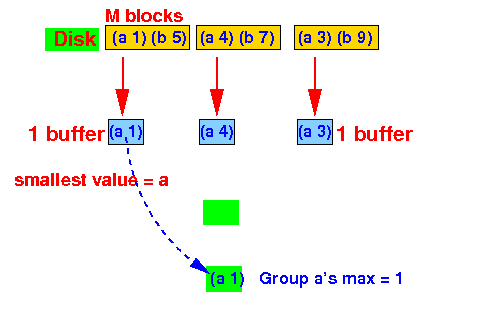
- Initialize the
first group:
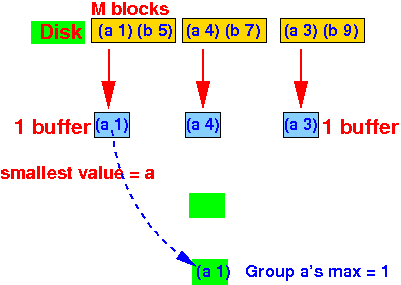
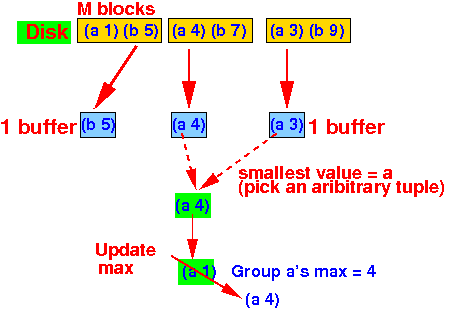
- As long as
the smallest grouping value = a,
we update the
maximum (= statistic):
- When the
the smallest grouping value
= b,
we output the
maximum (= statistic) and
start a
new group + statistic:
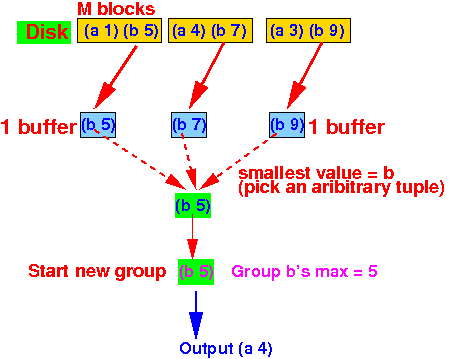
- Initialize the
first group:
- Input:
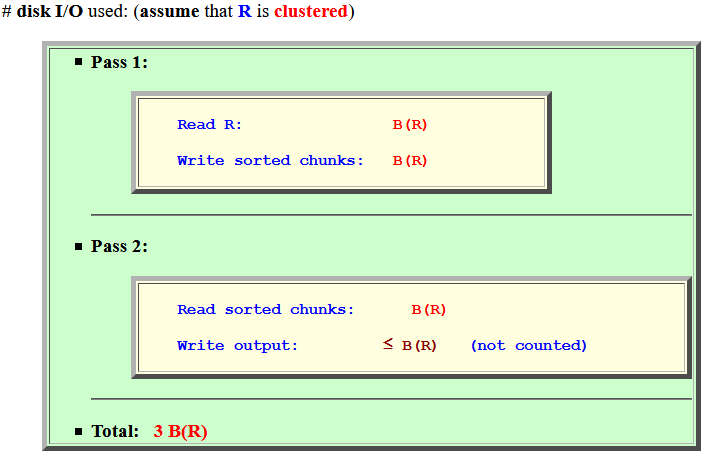
- # disk I/O used: (assume that
R is
clustered)
- Pass 1:
Read R: B(R) Write sorted chunks: B(R)
- Pass 2:
Read sorted chunks: B(R) Write output: ≤ B(R) (not counted)
- Total: 3 B(R)
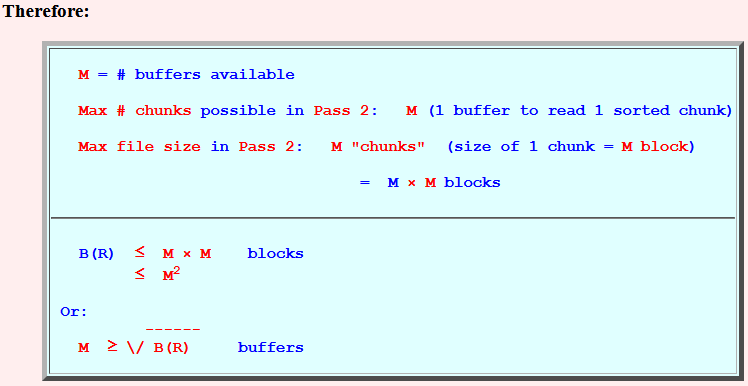
- Pass 1:
- Memory requirement:
- The relation R
can have at most
M chunks, because
in Pass 2:
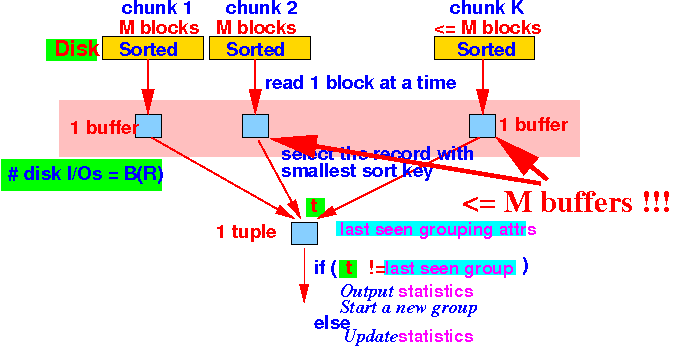
we can use ≤ M buffers (1 buffer for 1 chunk).
- Therefore:
B(R) ≤ M chunks (1 chunk = M blocks) B(R) ≤ M × M blocks ≤ M2 Or: ------ M ≥ \/ B(R) buffers
- The relation R
can have at most
M chunks, because
in Pass 2: