Slideshow:
The bag difference operator (−bag)
Comment: no search (hash) structure used because we do not have enought buffers !!!
The 2-pass TPMMS based bag difference
(−bag) algorithm
- Pass 1
(Graphically explained in next slide)
The 2-pass TPMMS based bag difference
(−bag) algorithm
- Pass 1
Use M buffers and sort the relation R and S into chunks of (sorted) M blocks:
IO cost for pass 1 = 2 B(R) + 2 B(S)
The 2-pass TPMMS based bag difference
(−bag) algorithm
- Pass 2
Pass 2:
(Graphically explained in next slide)
The 2-pass TPMMS based bag difference
(−bag) algorithm
- Pass 2
Pass 2:
You only need a program variable to store 1 tuple for each relation (i.e.: do not require an entire buffer)
The 2-pass TPMMS based bag difference
(−bag) algorithm
- Example
- Pass 1
Pass 1: read chunks of M blocks from relations R and S and sort:
Write the sorted chunks (each chunk is M blocks) to disk
The 2-pass TPMMS based bag difference
(−bag) algorithm
- Example
- Pass 2
(R and S are bags !)
Pass 2: read 1 block from every (sorted) chunk and find the smallest tuple in each relation:
If R(smallest tuple value) <
S(smallest tuple value) then
output R's tuple
and
advance R
(You can get multiple value if
the value occur multiple times in
R)
If R(smallest tuple value) =
S(smallest tuple value) then
discard R's tuple (subtract !) and
advance R and S
If R(smallest tuple value) >
S(smallest tuple value) then
(discard S's tuple) and
advance S
Cost analysis of
the 2-pass TPMMS based bag difference
(−bag) algorithm
Buffer requirement of
the 2-pass TPMMS based bag difference
(−bag) algorithm
The relation R and S together must have at most M chunks, because Pass 2 can use at most M buffers:
(We need to use 1 buffer to read 1 sorted chunk)
Buffer requirement of
the 2-pass TPMMS based bag difference
(−bag) algorithm
- Bag Difference operator:
R −B S - Example Bag Difference:
R = {1, 2, 2, 2, 3}; S = {2, 2, 3, 3, 4}; R −B S = { 1, 2 }
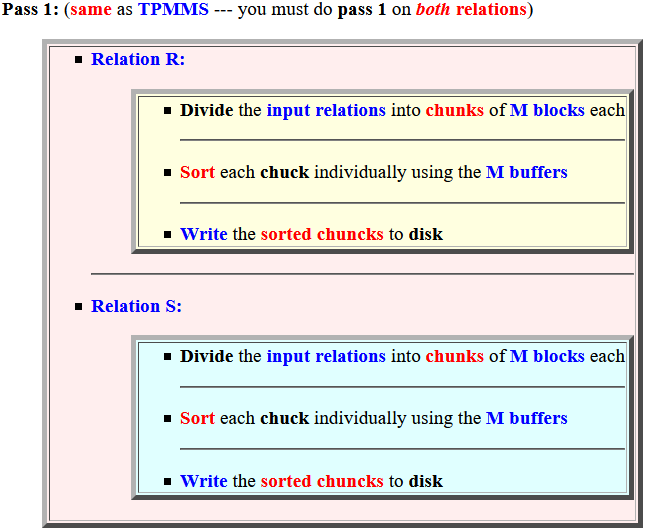
- Pass 1:
(same as
TPMMS ---
you must do Pass 1 on
both relations)
- Relation R:
- Divide the
input relations into
chunks of
M blocks each
- Sort each chuck
individually using the
M buffers
- Write the sorted chuncks to disk
- Divide the
input relations into
chunks of
M blocks each
- Relation S:
- Divide the
input relations into
chunks of
M blocks each
- Sort each chuck
individually using the
M buffers
- Write the sorted chuncks to disk
- Divide the
input relations into
chunks of
M blocks each
Graphically:
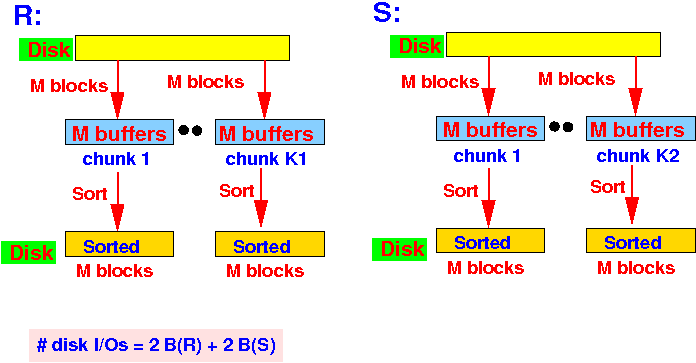
- Relation R:
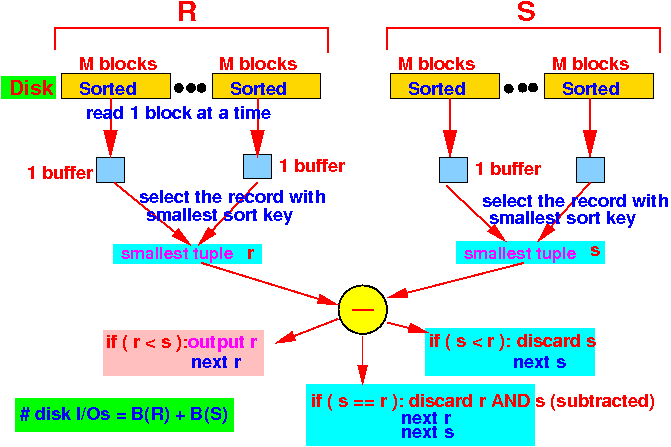
- Pass 2:
Use the M buffers to read sorted chunks from BOTH R and S
while ( R and S has tuples ) { r = tuple with the smallest sort key ∈ R; s = tuple with the smallest sort key ∈ S; if ( r < s ) { output r; // r did NOT get subtracted away !! next r; } else if ( s < r ) { next s; } else { discard r; // r gets subtracted away by s next r, s; } }Graphically:
- Example:
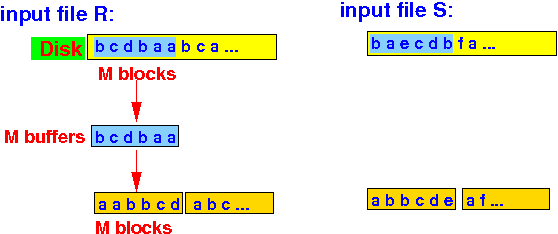
- Inputs:
- Pass 1: sort
chunks of size
M blocks
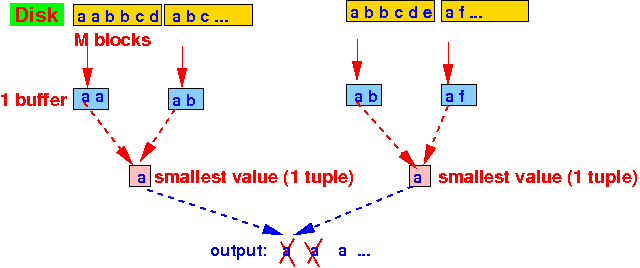
- Pass 2: remove
common tuples
to obtain
difference as
a bag
- Inputs:
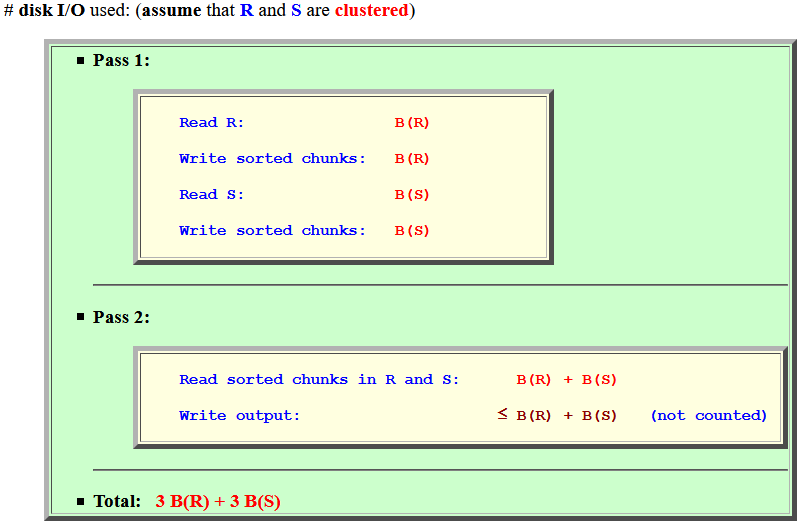
- # disk I/O used: (assume that
R is
clustered)
- Pass 1:
Read R: B(R) Write sorted chunks: B(R) Read S: B(S) Write sorted chunks: B(S)
- Pass 2:
Read sorted chunks in R and S: B(R) + B(S) Write output: ≤ B(R) + B(S) (not counted)
- Total: 3 B(R) + 3 B(S)
- Pass 1:
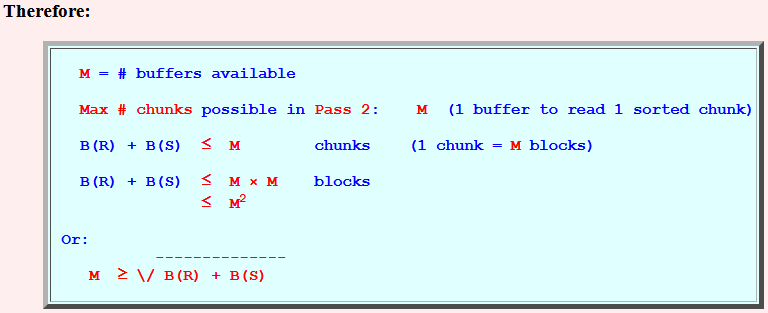
- Memory requirement:
- We can have at most
M chunks
in Pass 2:
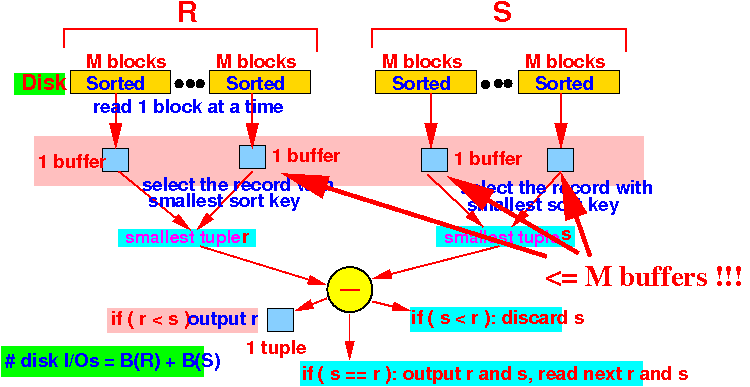
Therefore: total number of chunks of R and S --- together --- must be ≤ M
- Therefore:
B(R) + B(S) ≤ M chunks (1 chunk = M blocks) B(R) + B(S) ≤ M × M blocks ≤ M2 Or: -------------- M ≥ \/ B(R) + B(S)
- We can have at most
M chunks
in Pass 2: