Slideshow:
2-pass
hash based
algorithm for duplicate elimination
(δ)
-
pass 1
Organization: use 1 buffer to read R and (M−1) buffer to write Ri
Property of the tuples in a hash bucket
2-pass
hash based
algorithm for duplicate elimination
(δ)
-
pass 2
Performance cost
Buffer requirement -
key observation
Buffer requirement -
estimate size
Assumed size of each sub-relation:
Minimum buffer requirement: (derive using the fact that B(Ri) ≤ M−1)
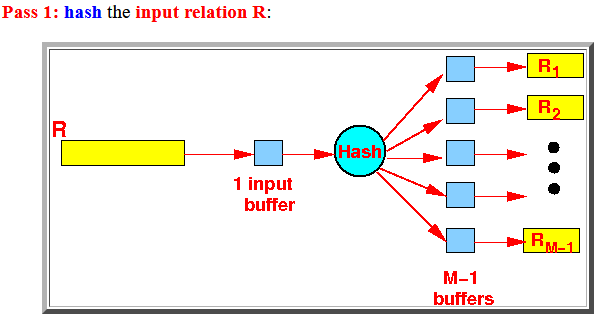
- Pass 1:
hash the
input relation R:
Notice that:
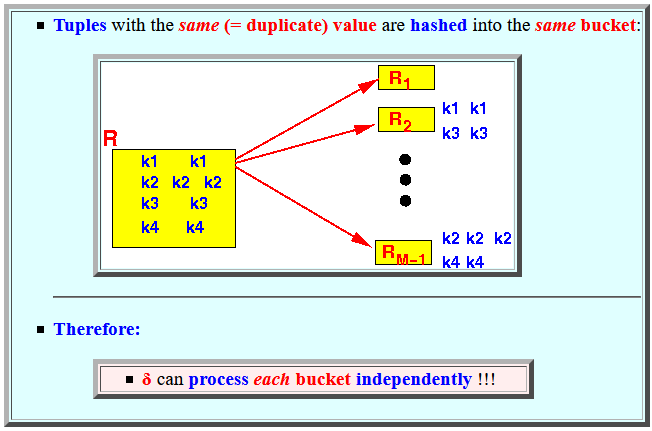
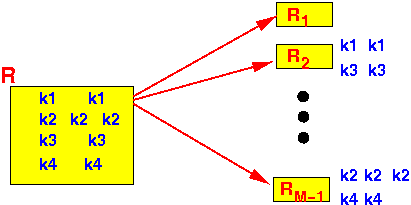
- Tuples with the
same (= duplicate) value
are hashed into the
same bucket:
- Therefore:
- δ can process each bucket independently !!!
- Tuples with the
same (= duplicate) value
are hashed into the
same bucket:
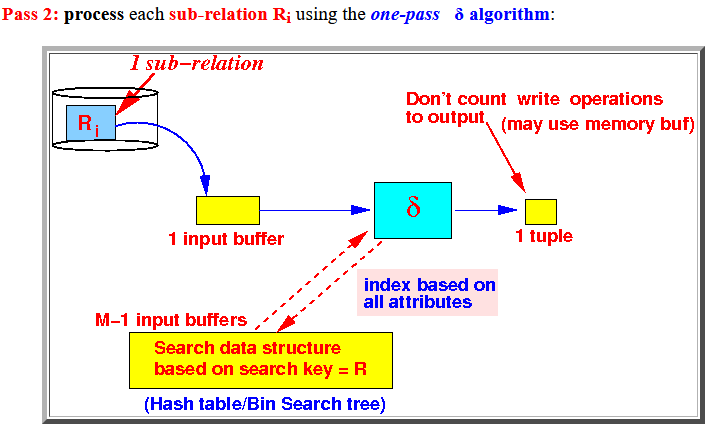
- Pass 2:
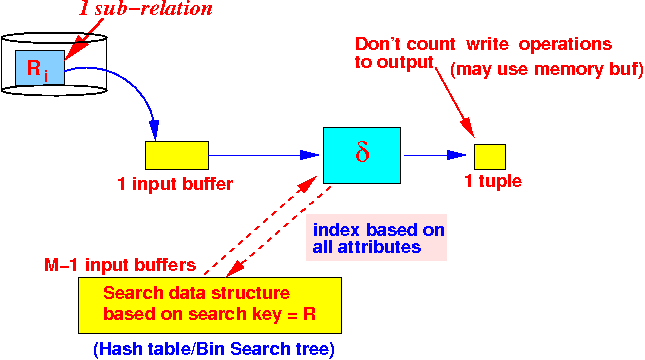
process each
sub-relation Ri
using the one-pass
δ algorithm:
- Cost incurred during
Phase 1:
Read R: B(R) Write M-1 buckets (total): B(R)
- Cost incurred during
Phase 2:
Read M-1 buckets (total): B(R) Write non-duplicate tuples: ≤ B(R) (not counted - use buffer to pass !)
- Total cost of the
δ(R) operation:
Cost of δ(R) = 3 B(R)
- The one-pass algorithm used
in Phase 2 has this
memory constraint:
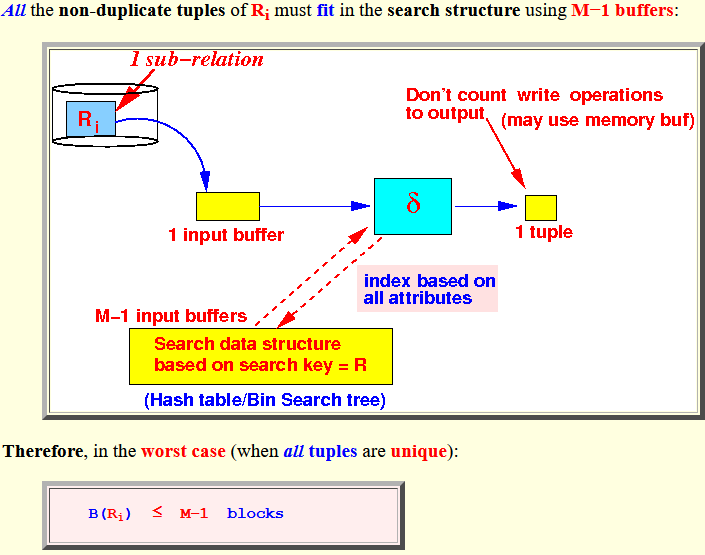
- All the
non-duplicate tuples of
Ri must
fit in the search structure
using
M−1 buffers:
Therefore, in the worst case (when all tuples are unique):
B(Ri) ≤ M−1 blocks
- The best case scenario
of the hashing is:
- Every sub-relation has
the same size:
1 B(Ri) = --- B(R) M-1(Otherwise, some sub-relation will larger than B(R)/(M−1) !!!)
Therefore:
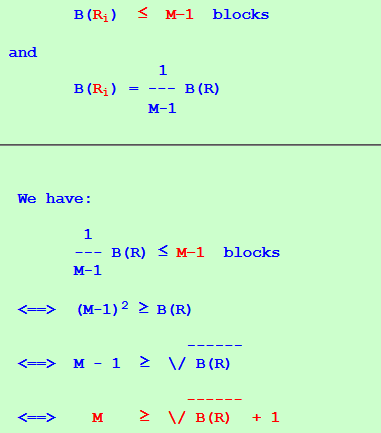
B(Ri) ≤ M−1 blocks and 1 B(Ri) = --- B(R) M-1
We have: 1 --- B(R) ≤ M−1 blocks M-1 <==> (M-1)2 ≥ B(R) ------ <==> M - 1 ≥ \/ B(R) ------ <==> M ≥ \/ B(R) + 1 - Every sub-relation has
the same size:
- All the
non-duplicate tuples of
Ri must
fit in the search structure
using
M−1 buffers:
- Note:
- You will often see
a simplified approximate bound
for the memory constraint:
------ M ≥ \/ B(R)because it is not neccessary to have exactly this amount of memory.
The result of a few buffers less is minimal thrashing (virtual memory will swap some buffers in/out to disk)
- You will often see
a simplified approximate bound
for the memory constraint: