Slideshow:
Do we need
to use multi-dimensional indexes ?
Case study on using B+-tree on multi-dimensional data
Index file used:
(1) B+-tree on the
x-coordinate of objects
Index file used:
(2) B+-tree on the
y-coordinate of objects
Process a range query using the
B+-tree indexes
How to use the B+-tree indexes to process the range query:
How to use the B+-tree indexes to process the range query:
Result: we found all coordinate records (x,y) where xL ≤ x ≤ xH:
How to use the B+-tree indexes to process the range query:
Do the same thing with the y-index file: find all coordinate records (x,y) where yL ≤ y ≤ yH:
How to use the B+-tree indexes to process the range query:
Compute the intersection of these 2 sets of records DB addresses (pointers):
The Database pointers in the intersection satisfy: xL ≤ x ≤ xH and yL ≤ y ≤ yH
Retrieve the records using this set of record pointers to answer to the range query
Question: what is the performance cost (= # disk IO needed) ?
IO cost of range query using B+-tree indexes
Data file statistics:
IO cost of range query using B+-tree indexes
Data file statistics:
( No disk I/O operation needed to read an internal node in the B+-tree index)
IO cost of range query using B+-tree indexes
Expected (average) # points selected in the output:
IO cost of range query using B+-tree indexes
Processing step 1: find the xL-coordinate:
#Disk IOs used = 0 (because we assumed internal nodes stored in memory)
IO cost of range query using B+-tree indexes
Processing step 2: traverse the x-index file between xL=450 and xH=550:
#record ptrs = ((550-540) ⁄ 1000) × 1,000,000 = 100,000 (because we assumed uniform distribution over 1 - 1000)
#Disk IOs used = 100,000 / 200 = 500 blocks (because we assumed 200 index recs per index blk)
IO cost of range query using B+-tree indexes
Processing step 3: do the same for the y-coordinate
#record ptrs = ((550-540) ⁄ 1000) × 1,000,000 = 100,000 (because we assumed uniform distribution over 1 - 1000)
#Disk IOs used = 100,000 / 200 = 500 blocks (because we assumed 200 index recs per index blk)
IO cost of range query using B+-tree indexes
Processing step 4: compute the intersection of these 2 sets of pointers
#Disk IOs used = 0 blocks (because all pointers were read in memory by previous 2 steps)
#record ptrs in intersection ~= 10,000 (the expected # points in the output - go 4 slides back if necessary)
IO cost of range query using B+-tree indexes
Processing step 5: retrieve the (10,000) records using the record ptrs in intersection
IO cost of range query using B+-tree indexes
Grand total:
Alternate solution: scan the
entire data file
(without using index)
Brute force search in the data file (without using the indexes):
Alternate solution: scan the
entire data file
(without using index)
The cost of the brute force search in the data file (without using the indexes):
Conclussion of this exercise...
- Question:
- Can our one-dimensional index technique support geometrical (2-dimensional) queries efficiently ???
- Case study:
- Let's try to process a range query using a B-tree index.....
- Database: object locations
Object( x, y, other-attributes ) // x and y are the // coordinates of the object
- Query:
- Find all objects that
lies with in a rectangle:
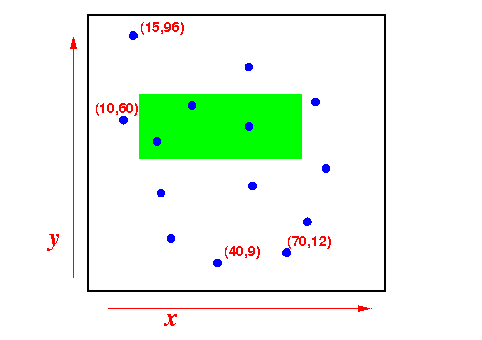
- Find all objects that
lies with in a rectangle:
- Suppose we have
B+-tree indexes on:
- The x-coordinate attribute of Object and
- The y-coordinate attribute of Object
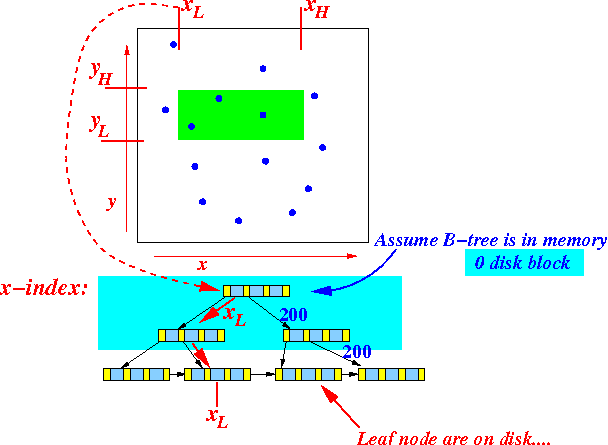
- The B+-tree on
the x-coordinate information
looks like this:
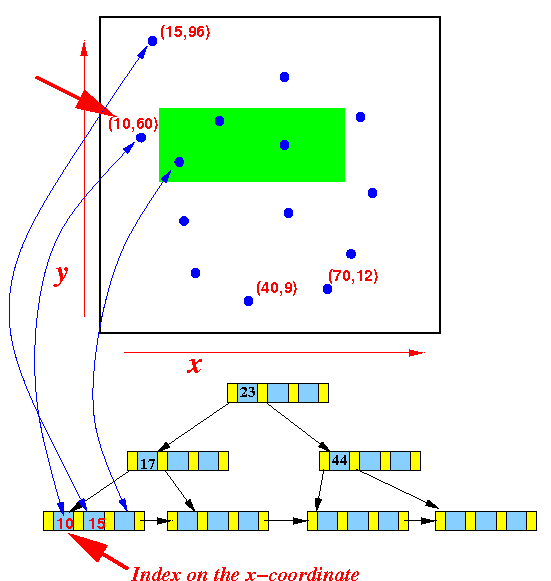
(The point with the smallest x-coordinate value is the left-most leaf key)
- The B+-tree on
the y-coordinate information
looks like this:
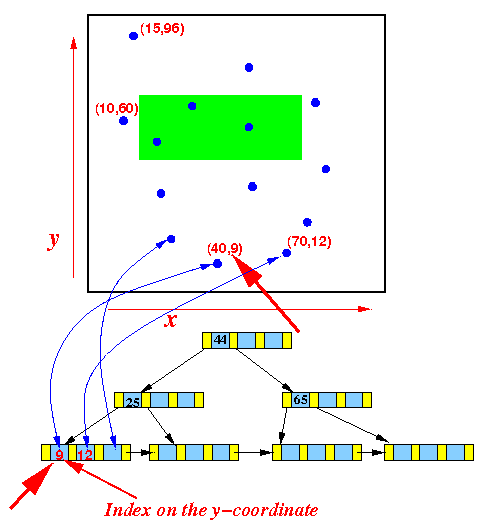
(The point with the smallest y-coordinate value is the left-most leaf key)
- Range query:
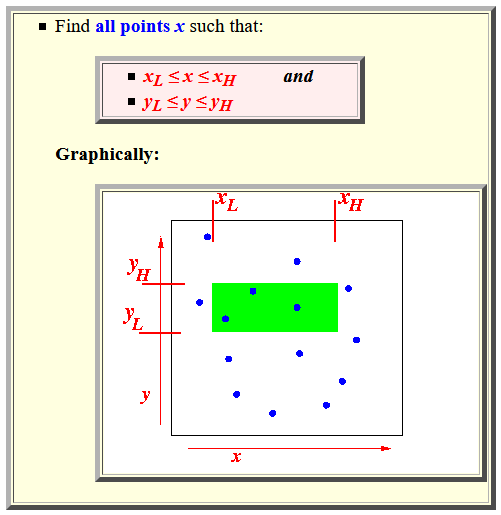
- Find all points x
such that:
- xL ≤ x ≤ xH and
- yL ≤ y ≤ yH
Graphically:
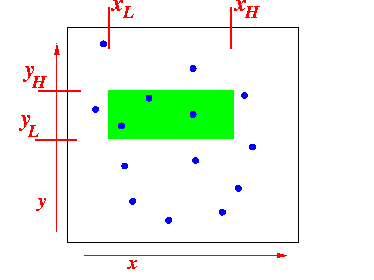
- Find all points x
such that:
- How to use
the B+-tree
indexes to
process the
range query:
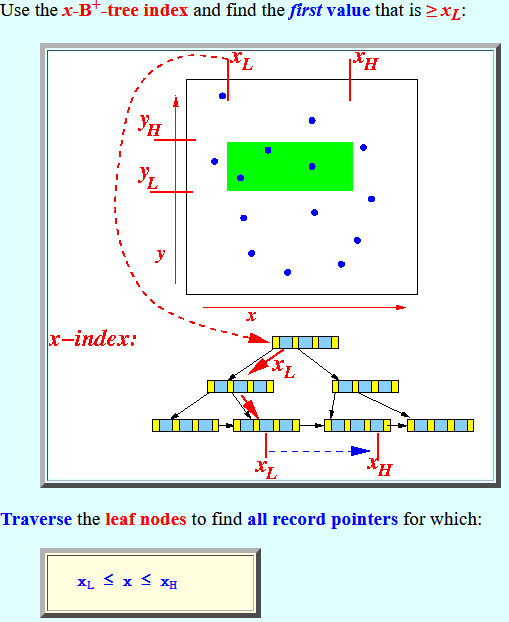
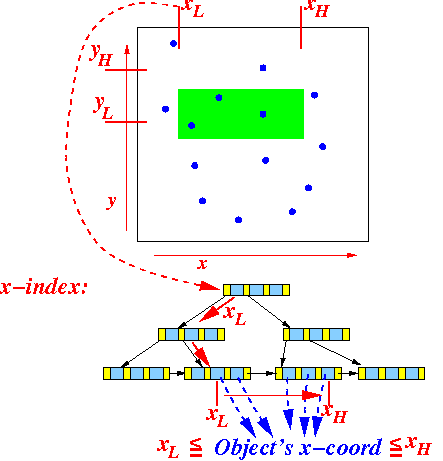
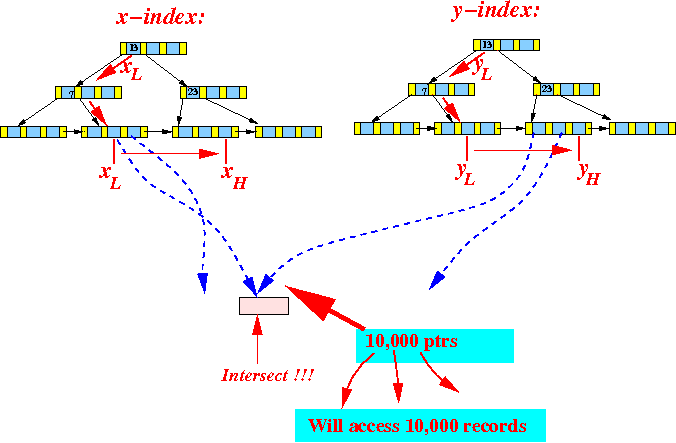
- Use the x-B+-tree index
and find
the first value
that is ≥ xL:
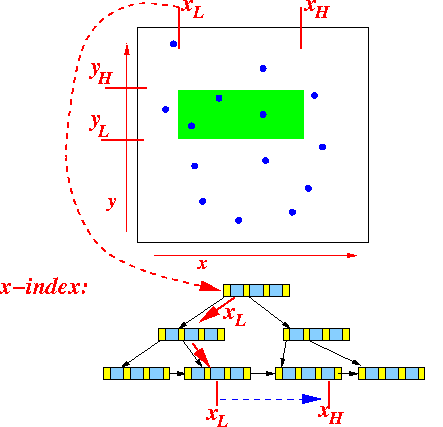
Traverse the leaf nodes to find all record pointers for which:
xL ≤ x ≤ xH
Graphically:
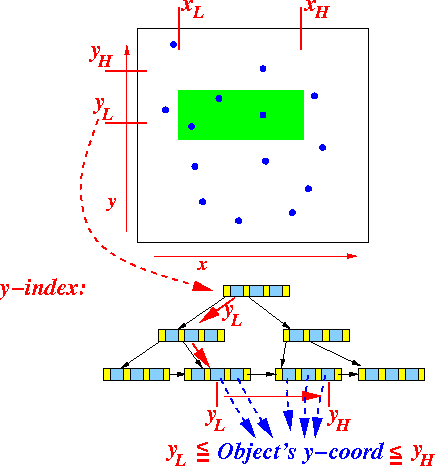
- Do the same for the
y-coordinate:
Graphically:
- Compute the intersection of the
2 pointer sets:
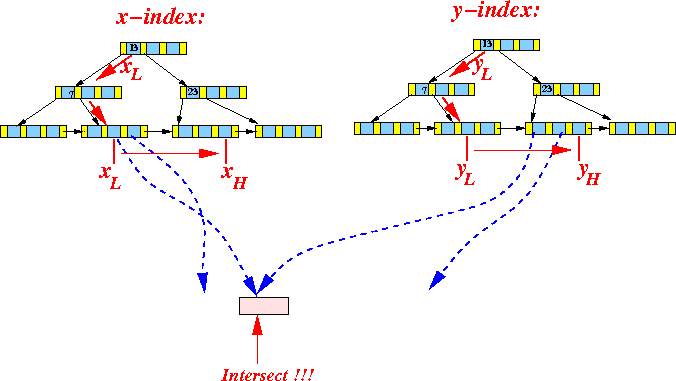
- Retrieve the
records using the
record pointers in the
intersection.
- These records are
guarantee to
satisfy:
- xL ≤ x ≤ xH and
- yL ≤ y ≤ yH
- These records are
guarantee to
satisfy:
- Use the x-B+-tree index
and find
the first value
that is ≥ xL:
- Sounds good....
no ???
- You will see that this is useless
This solution is not faster than scanning the entire relation !!!
- You will see that this is useless
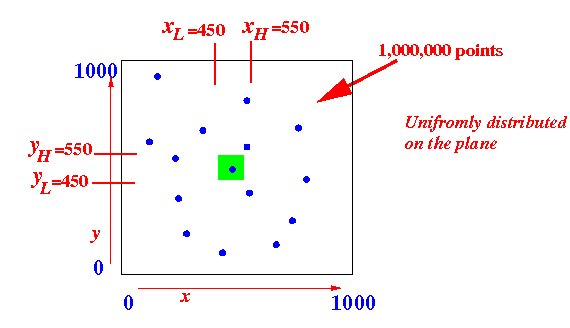
- Consider the following
situation:
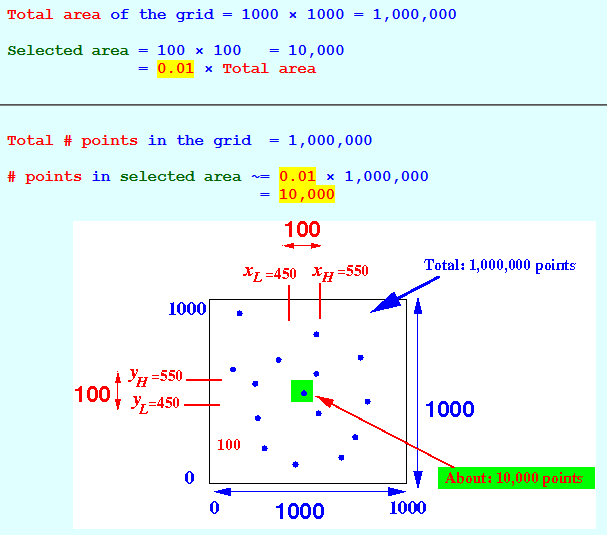
- We have a 1000×1000
grid
- There are 1,000,000 points
on the grid ---
we assume a
uniform distribution of
the points over the
grid
Query:
- Find all the points (x,y) within the square where 450 ≤ x ≤ 550 and 450 ≤ y ≤ 550
Graphically:
- We have a 1000×1000
grid
- First,
let's look at some statistics
about th einputs:
Total area of the grid = 1000 × 1000 = 1,000,000 Selected area = 100 × 100 = 10,000 = 0.01 × Total area
Total # points in the grid = 1,000,000 # points in selected area ~= 0.01 × 1,000,000 = 10,000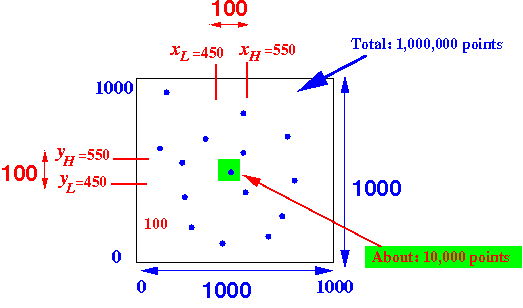
Other statistics: # points with x-coordinate in [450,550] ~= 0.1 × 1,000,000 = 100,000 # points with y-coordinate in [450,550] ~= 0.1 × 1,000,000 = 100,000
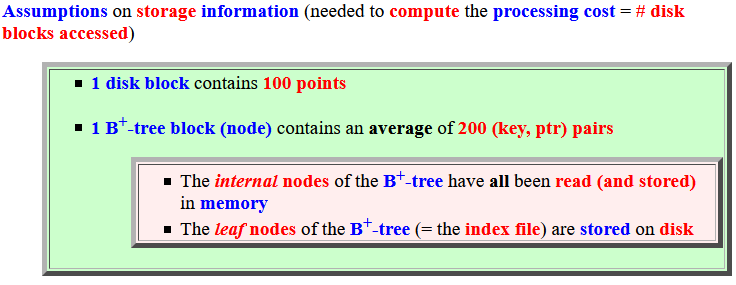
- Assumptions on
storage
information
(needed to compute the
processing cost
= # disk blocks accessed)
- 1 disk block contains
100 points
- 1 B+-tree block (node)
contains
an average of
200 (key, ptr) pairs
- The internal nodes of the B+-tree have all been read (and stored) in memory
- The leaf nodes of the B+-tree (= the index file) are stored on disk
- 1 disk block contains
100 points
- Computing the
processing cost
(= # disk blocks accessed)
to find all point in
the selected area:
- Use the x-coord B+-tree index
and find
the first value
that is ≥ xL:
Cost to find the database address of the B+ leaf node with xL = 450:
- Cost = 0
(Because we assume that the internal nodes of the B+ tree index are stored in memory)
- Cost = 0
- Starting at the
B+ node containing
the search key 450:
- Traverse the
leaf nodes to find
all record pointers for which:
450 ≤ x ≤ 550
Graphically:
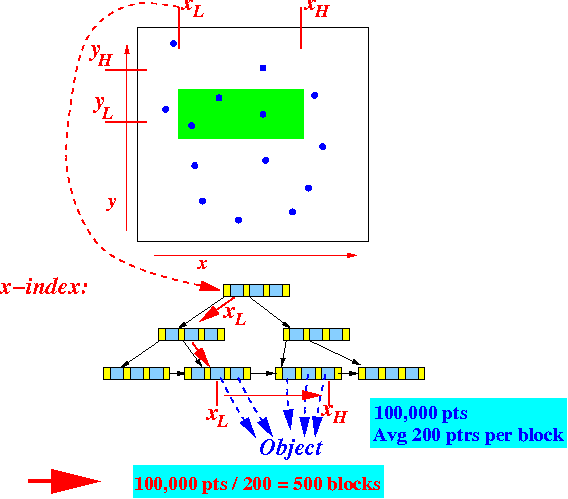
We will access approximately 0.1 × 1,000,000 = 100,000 search keys
The cost to access 100,000 search keys (stored in leaf nodes of the B+-tree) is:
- # B+ leaf nodes that we
must access:
Read: 100,000 search keys (200 search keys per leaf node) = 500 leaf nodes (= index blocks)
- Cost to access the x-coord B+-tree = 500 disk block
- Traverse the
leaf nodes to find
all record pointers for which:
- We must
do the same for the
y-coordinate:
Graphically:
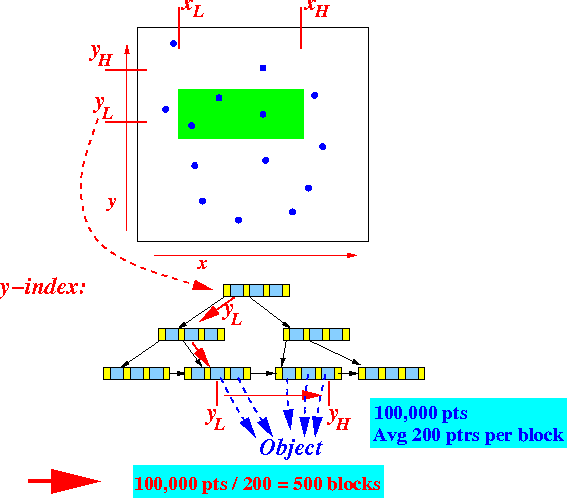
So: cost to access the y-coord B+-tree = 500 disk block
- Compute the intersection of the
2 "search key" sets:
Cost of this step:
- Cost = 0
Because no disk access is required
The intersection will contain approximately 10,000 (= 0.01 × 1,000,000) record pointers (database addresses) to points (records)
- Cost = 0
- We must then retrieve the
point records using the
10,000 record pointers in the
intersection:
-
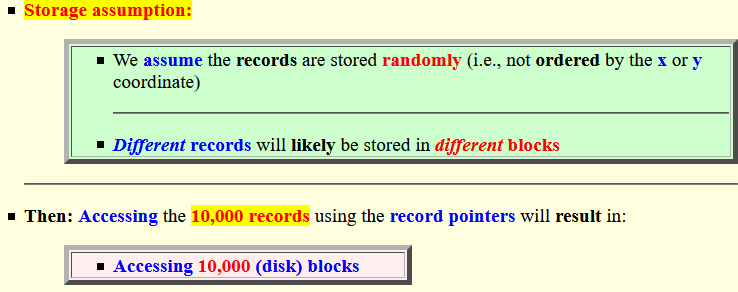
Storage assumption:
- We assume the
records are stored
randomly
(i.e., not ordered by the
x or
y coordinate)
- Different records will likely be stored in different blocks
- We assume the
records are stored
randomly
(i.e., not ordered by the
x or
y coordinate)
- Then:
Accessing the
10,000 records using
the record pointers will
result in:
- Accessing 10,000 (disk) blocks
-
Storage assumption:
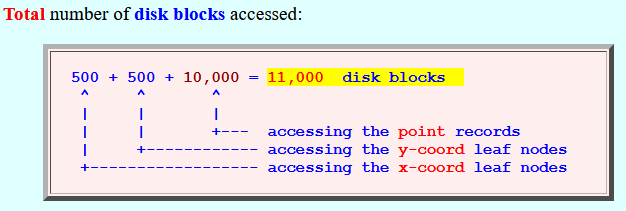
- Total number of
disk blocks accessed:
500 + 500 + 10,000 = 11,000 disk blocks ^ ^ ^ | | | | | +--- accessing the point records | +------------ accessing the y-coord leaf nodes +------------------ accessing the x-coord leaf nodes
Comment:
- The number index
disk blocks accessed
is usually
much smaller than
the
number data
disk blocks accessed !!!
- We can often discard the index blocks if we want to approximate the number of disk blocks accessed by an operation !!!
Alternate solution
- Use the x-coord B+-tree index
and find
the first value
that is ≥ xL:
- Suppose:
- We do not have any index on the points records....
How to find all point in the selected region:
while ( not EOF ) { Read next data block; // Scan ALL data blocks !! for ( each point (x,y) ∈ data block ) { if ( 450 ≤ x ≤ 550 && 450 ≤ y ≤ 550 ) Output (x,y); } }
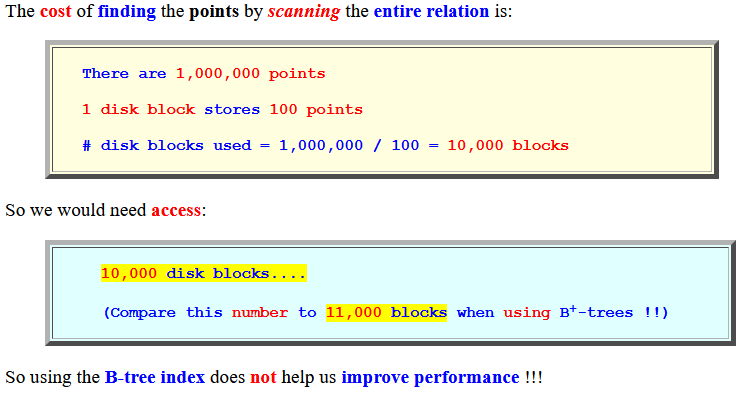
- The cost of
finding the
points by
scanning the
entire relation is:
There are 1,000,000 points 1 disk block stores 100 points # disk blocks used = 1,000,000 / 100 = 10,000 blocks
So we would need access:
10,000 disk blocks.... (Compare this number to 11,000 blocks when using B+-trees !!)So using the B-tree index does not help us improve performance !!!
- Conclusion:
- We cannot store
geographically "related" data
randomly
- If related geographical data is store randomly, we will need to access too many data blocks !!!
Lesson:
- We must store geographically "related" data (i.e.: points that are close to each other) in the same data block !!!
- To support
the access
to the geometrical data:
- We also need a more appropriate index structure for multi-dimensional data !!!
- We cannot store
geographically "related" data
randomly