Slideshow:
Weakness of the Extensible Hashing technique
The Linear Hashing technique was proposed to address this weakenss
Overview of the Linear Hashing technique
Linear Hashing is based on Extensible Hashing !!!
Linear Hashing uses a clever logical hash index → physical hash index mapping function
Modifying the
logical index → physical index
of the Extensible Hashing technique
Recall the bucket size doubling technique of Extensible hashing:
Suppose we increase i = i + 1 and double the logical hash bucket size....
Modifying the
logical index → physical index
of the Extensible Hashing technique
We can fix the hash index using this logical index → physical index mapping:
Modifying the
logical index → physical index
of the Extensible Hashing technique
Take a good look at the logical index → physical index map:
Can you find (think of) a function that you can use to perform the same mapping operation ?
(Reason:: if you can find such a function, then you don't need to store the map using array elements !!)
Modifying the
logical index → physical index
of the Extensible Hashing technique
If we can find such a mapping function:
We don't need to store the map using array elements in order to double the logical hash table size !!
Modifying the
logical index → physical index
of the Extensible Hashing technique
We can map the new array index to an existing array index:
If hash index x ≤ 011 (binary), we use the block pointer in the logical bucket[ x ]
If hash index x ≥ 100 (binary), we use the block pointer in the logical bucket[ suffix-1(x) ]
where: suffix-1(x) = x − 2⌊log(x)⌋
What does the suffix-1( x ) do:
Suffix-1(x) removes the leading 1 bit from the binary number x
My terminology: "virtual" hash bucket
"Virtual" hash bucket:
For a "virtual" hash bucket x, we use suffix-1(x) to map to a (real) logical hash bucket:
How to use Suffix-1( ) function
to double the
logical hash table size
Initial state: (the hash function uses (i − 1) bits )
How to use Suffix-1( ) function
to double the
logical hash table size
Suppose we double the hash index range (the hash function uses i bits)
How to use Suffix-1( ) function
to double the
logical hash table size
If x is a real logical hash bucket: use LogicalBucket[x] to find physical hash bucket
How to use Suffix-1( ) function
to double the
logical hash table size
If x is a "virtual" logical hash bucket: use LogicalBucket[Suffix-1(x)] to find physical hash bucket
How to
increase the
physical hash table
gradually using the new mapping technique
Initial state:
How to
increase the
physical hash table
gradually using the new mapping technique
After doubling the logical hash table (i.e.: increase the parameter i):
How to
increase the
physical hash table
gradually using the new mapping technique
We can add a new physical bucket (100) and adjust the logical → physical map:
Problem: the keys that hashes to 100 can no longer be found !!
How to
increase the
physical hash table
gradually using the new mapping technique
How to fix the problem: re-hash the keys in bucket[Suffix-1(x)]
How to
tell if
a (logical) hash index is
a real or virtual
logical hash bicket ?
- Main
disadvantage of
Extensible Hashing:
- The size of the
bucket array
will double each time
the
parameter i
incresses by 1
- This exponential growth rate is too fast
- The size of the
bucket array
will double each time
the
parameter i
incresses by 1
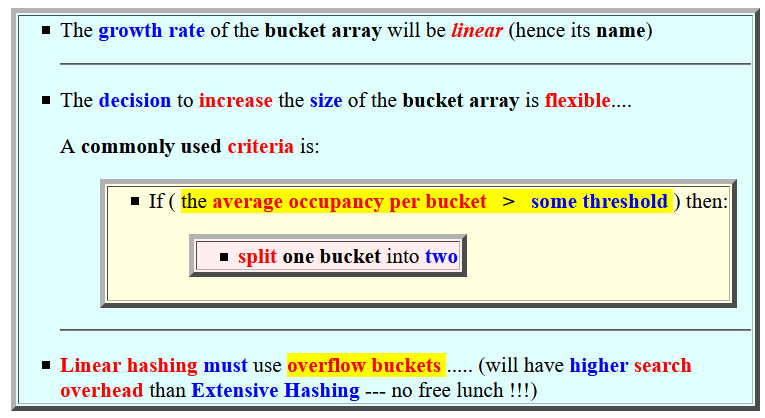
- Properties of the
Linear Hashing technique:
- The growth rate of
the bucket array will be
linear
(hence its name)
- The decision to
increase the
size of the
bucket array is
flexible....
A commonly used criteria is:
- If (
the average occupancy per bucket
>
some threshold
) then:
- split one bucket into two
- If (
the average occupancy per bucket
>
some threshold
) then:
- Linear hashing must use overflow buckets ..... (will have higher search overhead than Extensive Hashing --- no free lunch !!!)
- The growth rate of
the bucket array will be
linear
(hence its name)
-
Recall the
bucket doubling
technique
used in
Extensible Hashing:
- Before
doubling
the logical hash table:
- Extensive Hashing allow us
to increase (= double)
the hash function range
(= table size)
After doubling the logical hash table:
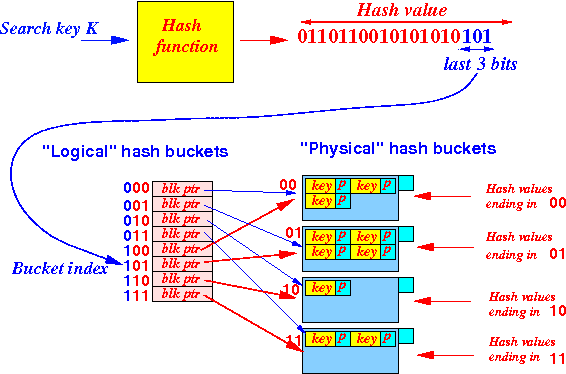
- Before
doubling
the logical hash table:
- Notice that:
- We increased the
hash function range
by
implement:
- A mapping of new hash keys in the additional range to the physical hash table
Graphically:
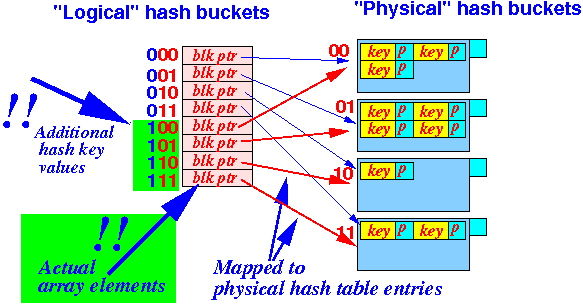
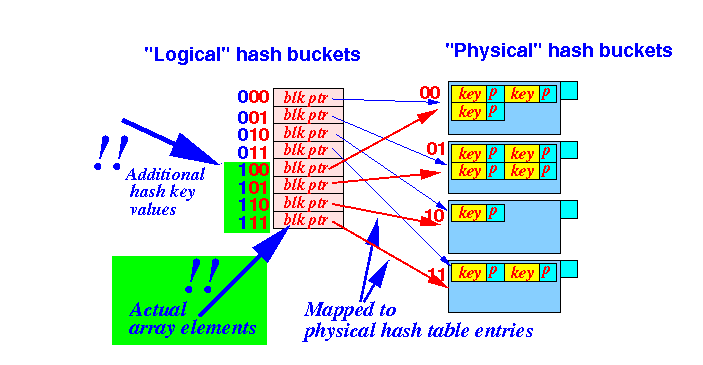
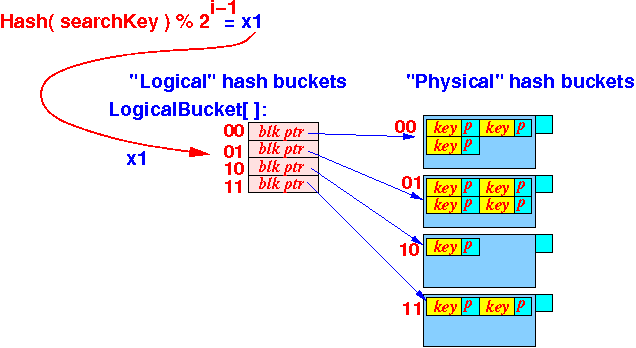
Idea:
- Do not use
real
hash buckets (= array elements)
- Use virtual hash buckets:
- Virtual bucket = a number that represents a hash bucket
- We use a mapping function
to map the
virtual hash buckets to
a physical hash bucket
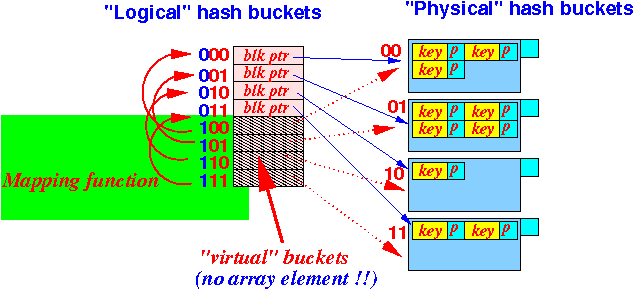
The mapping function in the above example is as follows:
100 ⇒ 0 101 ⇒ 1 110 ⇒ 10 111 ⇒ 11 Or: 100 ⇒ 00 101 ⇒ 01 110 ⇒ 10 111 ⇒ 11
- We increased the
hash function range
by
implement:
- Define the following
mapping function:
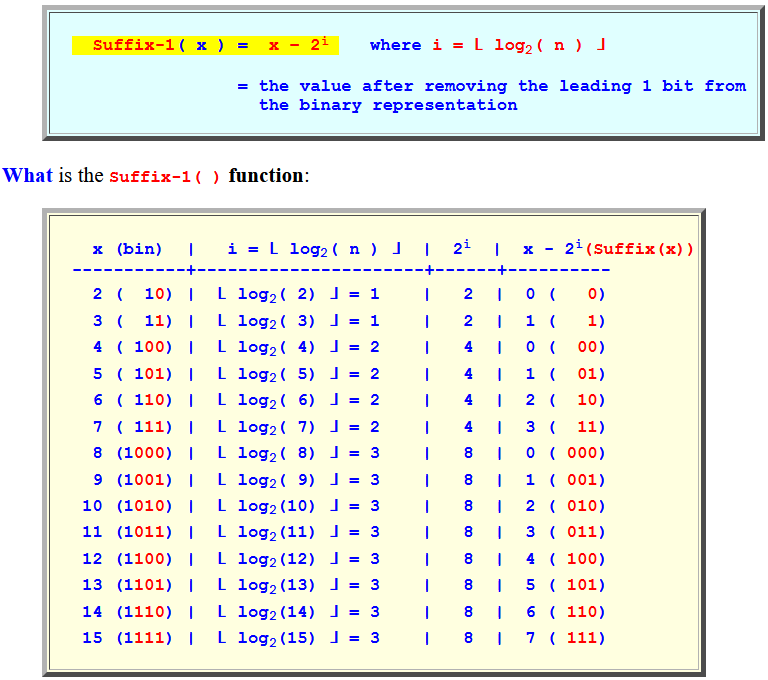
Suffix-1( x ) = x − 2i where i = ⌊ log2( n ) ⌋ = the value after removing the leading 1 bit from the binary representationWhat is the Suffix-1( ) function:
x (bin) | i = ⌊ log2( n ) ⌋ | 2i | x - 2i(Suffix(x)) -----------+----------------------+------+---------- 2 ( 10) | ⌊ log2( 2) ⌋ = 1 | 2 | 0 ( 0) 3 ( 11) | ⌊ log2( 3) ⌋ = 1 | 2 | 1 ( 1) 4 ( 100) | ⌊ log2( 4) ⌋ = 2 | 4 | 0 ( 00) 5 ( 101) | ⌊ log2( 5) ⌋ = 2 | 4 | 1 ( 01) 6 ( 110) | ⌊ log2( 6) ⌋ = 2 | 4 | 2 ( 10) 7 ( 111) | ⌊ log2( 7) ⌋ = 2 | 4 | 3 ( 11) 8 (1000) | ⌊ log2( 8) ⌋ = 3 | 8 | 0 ( 000) 9 (1001) | ⌊ log2( 9) ⌋ = 3 | 8 | 1 ( 001) 10 (1010) | ⌊ log2(10) ⌋ = 3 | 8 | 2 ( 010) 11 (1011) | ⌊ log2(11) ⌋ = 3 | 8 | 3 ( 011) 12 (1100) | ⌊ log2(12) ⌋ = 3 | 8 | 4 ( 100) 13 (1101) | ⌊ log2(13) ⌋ = 3 | 8 | 5 ( 101) 14 (1110) | ⌊ log2(14) ⌋ = 3 | 8 | 6 ( 110) 15 (1111) | ⌊ log2(15) ⌋ = 3 | 8 | 7 ( 111)Conclussion:
Suffix-1(x) returns the suffix of x after removing the leading 1 bit from x Suffix-1( 10 ) = 0 Suffix-1( 11 ) = 1 Suffix-1( 100 ) = 00 Suffix-1( 101 ) = 01 Suffix-1( 110 ) = 10 Suffix-1( 111 ) = 11 Suffix-1( 1000 ) = 000 Suffix-1( 1001 ) = 001 Suffix-1( 1010 ) = 010 Suffix-1( 1011 ) = 011 ...
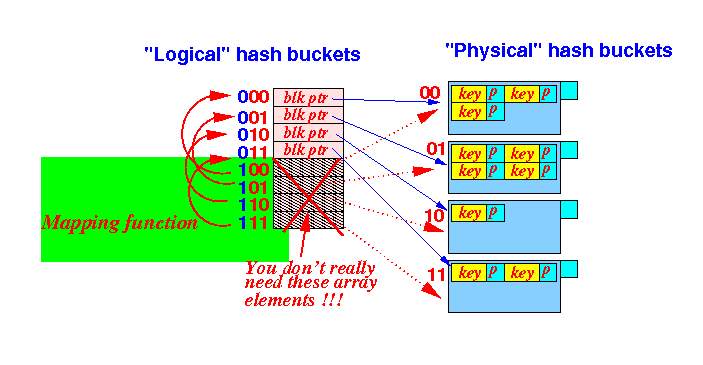
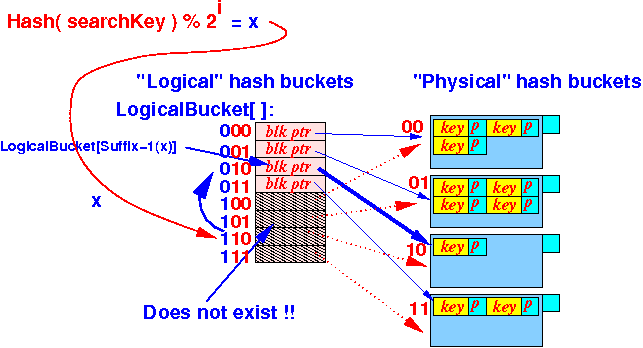
- How to
use the
Suffix-1( ) function
to
map
the virtual
logical hash buckets to
physical hash buckets:
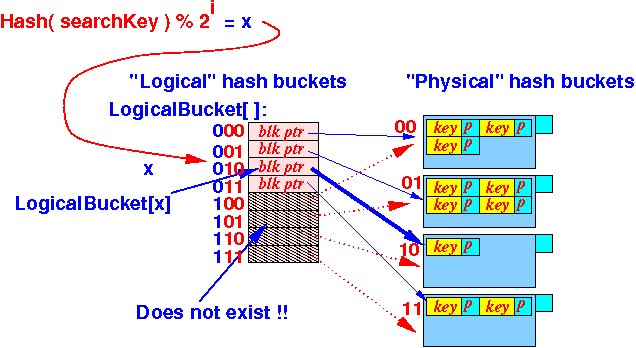
- Let
x =
the logical hash function value
obtained by
hashing a
search key
- x = a logical hash bucket index
- If
bucket x is
not virtual then use
the block pointer
to locate the
physical
hash bucket (= data block):
LogicalBucket[ x ] - If
bucket x is
virtual then use
the following (computed/mapped)
block pointer
to locate the
physical
hash bucket (= data block):
LogicalBucket[ Suffix-1( x ) ]Graphiscally explained:
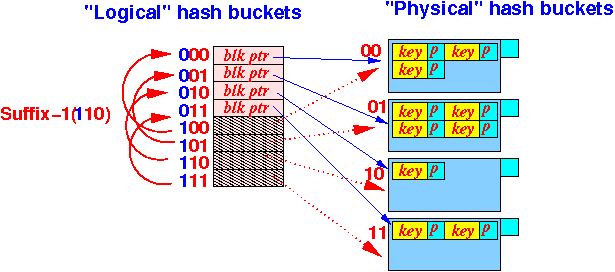
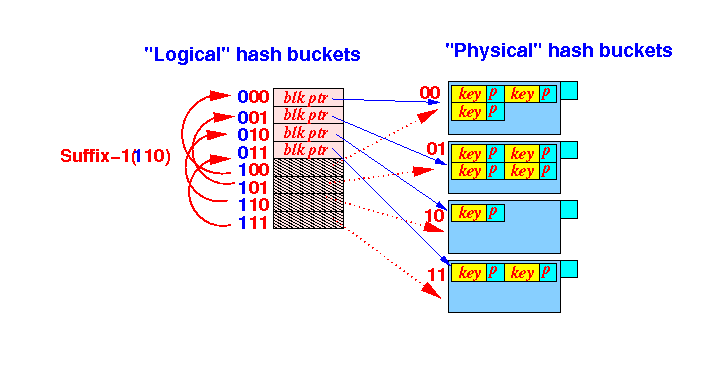
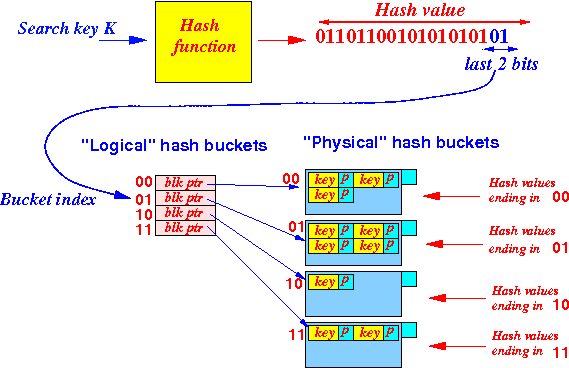
- Let
x =
the logical hash function value
obtained by
hashing a
search key
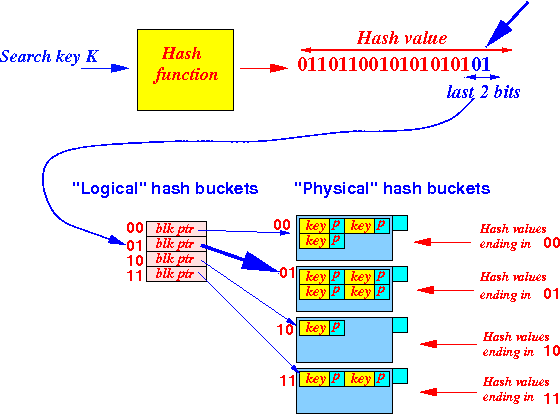
- Suppose we
are currently using
the last 2 bits
of the hash value:
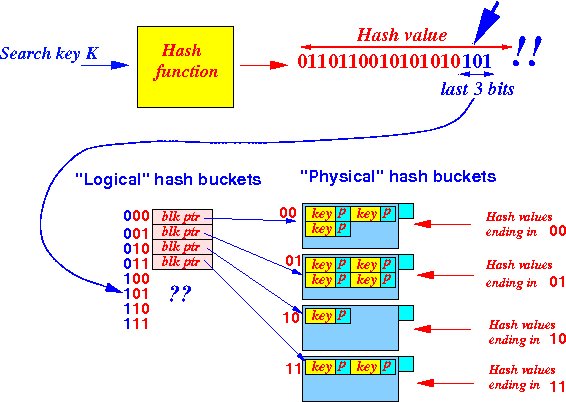
- Suppose we
double the
logical hash buckets
by using
the last 3 bits of
the hash value:
We can locate the search key in the hash index using the Suffix-1( ) function as follows:
Note:
- The logical hash table
still has
4 array elements
I.e.:
- We do not have to double the array size to fix the change in hash function range !!!
- The logical hash table
still has
4 array elements
- What happens in
Linear Hashing when we make a
virtual (logical) hash bucket
into a
"real" (logical) hash bucket:
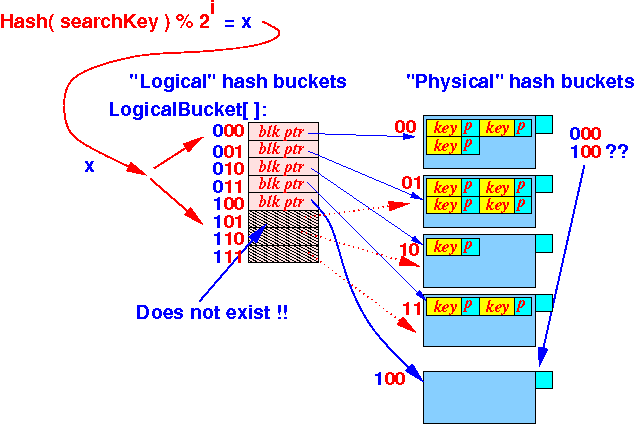
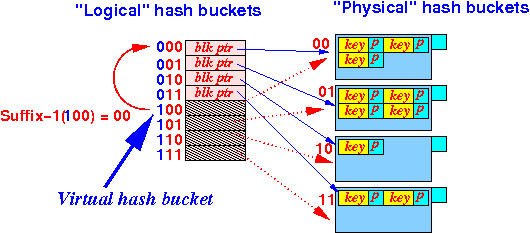
- Before:
the logical hash bucket 100
is virtual:
- If
the logical hash bucket 100
becomes an actual array element
(= non-virtual), then
it will
point to
a (new) physical hash bucket:
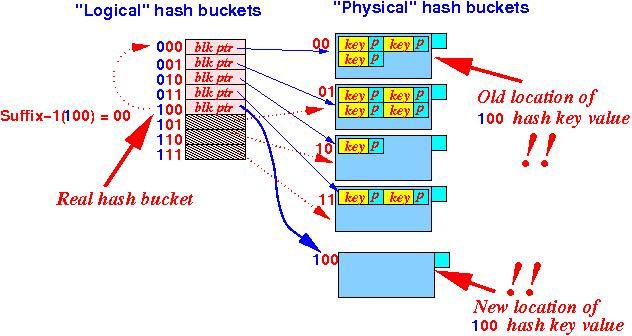
Where:
- The new physical hash bucket (disk block) will be used to store search keys that hash to 100
Notice that:
- Some of the search keys that hash to 100 are (still) stored in the physical hash bucket 00 !!!!!
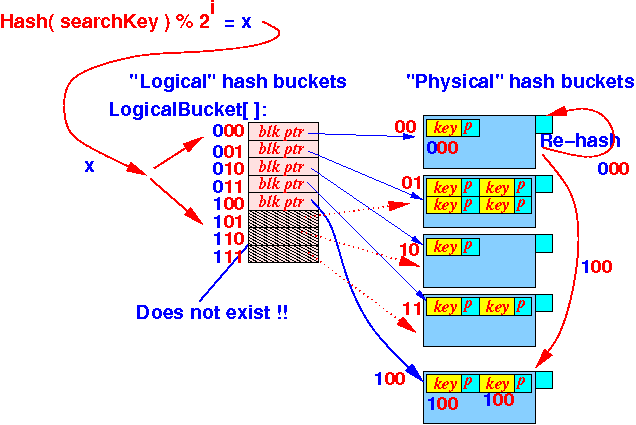
- Solution:
- Re-hash all the
search keys in
bucket
Suffix( 100 )
(= bucket 00)
- Re-hash all the
search keys in
bucket
Suffix( 100 )
(= bucket 00)
- Before:
the logical hash bucket 100
is virtual:
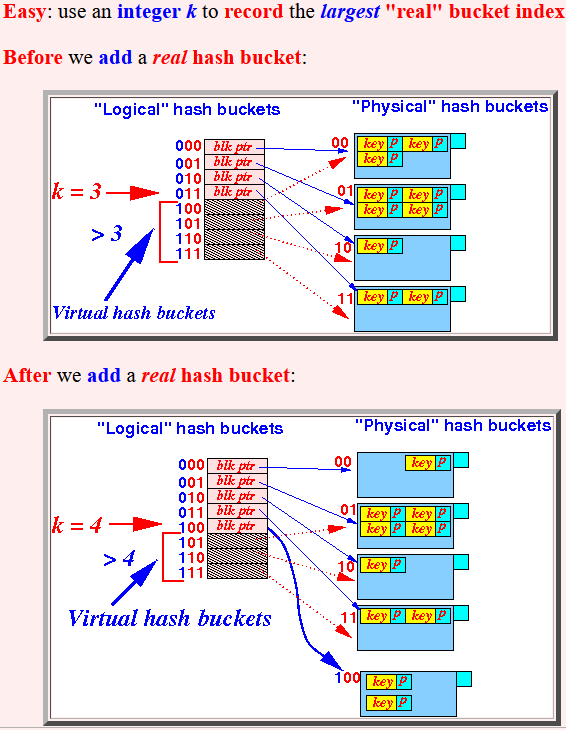
- How to tell
if a bucket is
real/virtual:
- Easy:
use an integer k
to record the
largest
"real" bucket index
Before we add a real hash bucket:
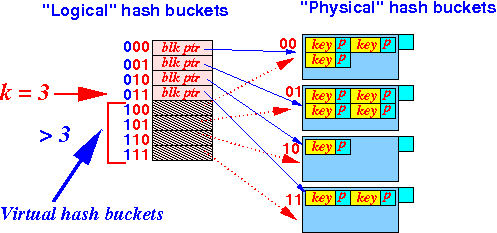
After we add a real hash bucket:
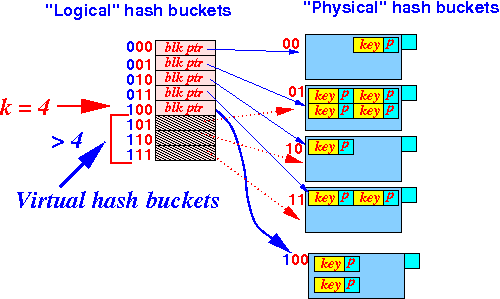
- Easy:
use an integer k
to record the
largest
"real" bucket index