Slideshow:
- Insert Algorithm for an object
ObjID:
- The insert algorithm in the
R-tree is
very similar to
the insert algorithm in the
B-tree
- The search key + record pointer
index entry is
always inserted
into a leaf node
- There is an
insert algoithm for
leaf nodes
(that keep the R-tree
balanced)
- There is an insert algoithm for internal nodes (that keep the R-tree balanced)
- The search key + record pointer
index entry is
always inserted
into a leaf node
- I (and the book) will only discuss the insert algorithm for leaf nodes
- The insert algorithm in the
R-tree is
very similar to
the insert algorithm in the
B-tree
- Inserting an
object in an
R-tree:
- Just like
the B-tree:
- The leaf nodes of the R-tree contains the object (record) pointers
- When you insert an
object, then:
- The object is always inserted into an leaf node !!!
- Just like
the B-tree:
- Insert algorithm
(to insert an object into
a leaf node of the
R-tree):
- The insert algorithm is
called using:
Insert( (MBB, ObjID), root ) ; // Insert Object (MBB, ObjID) in // the R-tree MBB = Min. Bounding Box of object ObjID = Object ID (e.g.: record pointer) root = root node of the R-tree
Insert Algorithm: (to insert an new object (mbb, ObjID) into a leaf node of the R-tree)
/* ================================================ Insert( (mbb,ObjID), n) (mbb,ObjID) = object with given mbb n = current node of operation ================================================= */ Insert( (mbb, ObjID), n ) { // n = current node of the search in the R-tree if ( n == internal node ) { for ( each entry ( BB, childptr ) in node n ) do { /* ====================================================== Insert the object in subtree of the first BB that contains the mbb of the inserted object ====================================================== */ if ( mbb of inserted object ⊆ BB ) { Situation: /* ----------------------------------------------
Insert the object in this subtree !!!
---------------------------------------------- */
Insert( (mbb,ObjID), childptr); // Insert !!
/* ----------------------------------------------
The recursion WILL have inserted the object !
---------------------------------------------- */
return; // Terminates the for-loop !!!
}
}
/* *********************************************************
We can ONLY reach here when EVERY BB (Bounding Box)
in the node n does not contain the object !!!
We enlarge one of the BB so it can index the new object
********************************************************* */
Find a BB in n such that:
Enlarging BB to contain the new object will add
the least amount of area to the bounding box BB
/* ----------------------------------------------
Insert the object in this subtree !!!
---------------------------------------------- */
Insert( (mbb,ObjID), childptr); // Insert !!
/* ----------------------------------------------
The recursion WILL have inserted the object !
---------------------------------------------- */
return; // Terminates the for-loop !!!
}
}
/* *********************************************************
We can ONLY reach here when EVERY BB (Bounding Box)
in the node n does not contain the object !!!
We enlarge one of the BB so it can index the new object
********************************************************* */
Find a BB in n such that:
Enlarging BB to contain the new object will add
the least amount of area to the bounding box BB
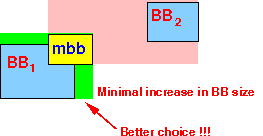 Update this BB in n to the Enlarged BB;
(Note: We do not need to update the BB in the parent node
because THAT BB contains the insert object)
/* ======================================================
Now the enlarged BB contains the object !!!
====================================================== */
Insert( (mbb,ObjID), childptr); // Insert in subtree !!
return; // Done
}
else // We reached a leaf node
{
/* =================================================
We found the leaf node to hold the object !!!
================================================= */
if ( leaf node has space to hold object )
{
insert (mbb, ObjID) in the leaf node;
}
else
{
Split the objects in the leaf node into set1 and set2;
// Set1 and set2 are 2 set of objects
// How to split the objects is a new subproblem...
Find the bounding box BB1 for set1 of the objects;
Find the bounding box BB2 for set2 of the objects;
// You will have 2 bounding boxes
Replace the parent's (BB, ptr) by (BB1, set1) and (BB2, set2);
(This step can cause the parent node to overflow !!!
We will need to split the parent node into 2 internal nodes
You will use a Insert procedure into an internal node
- just like the B-tree algorithm !!)
}
}
}
Update this BB in n to the Enlarged BB;
(Note: We do not need to update the BB in the parent node
because THAT BB contains the insert object)
/* ======================================================
Now the enlarged BB contains the object !!!
====================================================== */
Insert( (mbb,ObjID), childptr); // Insert in subtree !!
return; // Done
}
else // We reached a leaf node
{
/* =================================================
We found the leaf node to hold the object !!!
================================================= */
if ( leaf node has space to hold object )
{
insert (mbb, ObjID) in the leaf node;
}
else
{
Split the objects in the leaf node into set1 and set2;
// Set1 and set2 are 2 set of objects
// How to split the objects is a new subproblem...
Find the bounding box BB1 for set1 of the objects;
Find the bounding box BB2 for set2 of the objects;
// You will have 2 bounding boxes
Replace the parent's (BB, ptr) by (BB1, set1) and (BB2, set2);
(This step can cause the parent node to overflow !!!
We will need to split the parent node into 2 internal nodes
You will use a Insert procedure into an internal node
- just like the B-tree algorithm !!)
}
}
}
- The insert algorithm is
called using:
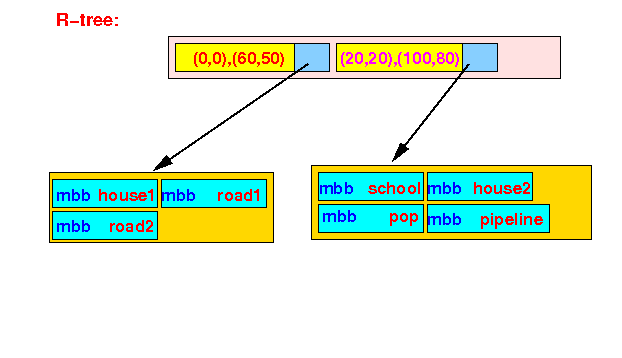
- Insert example 1:
easy case
(leaf node has space
for object)
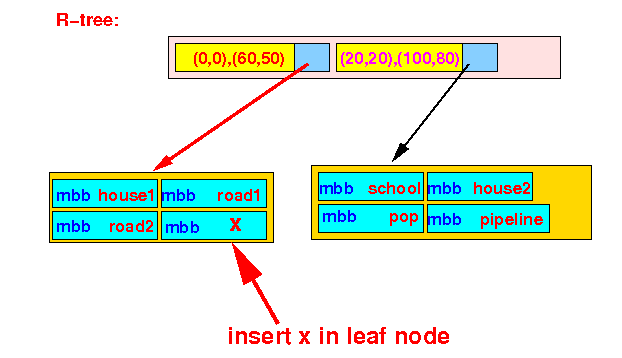
- Insert the object x
into the R-tree:
Steps of the Insert Algorithm:
- The first BB contains
x:
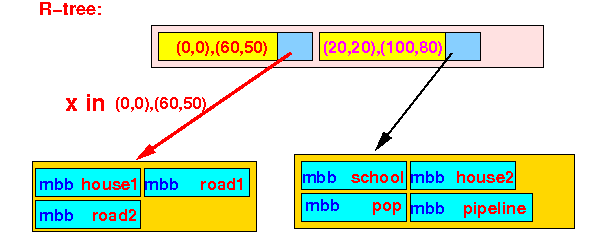
- Because there is space in
the leaf node,
we insert the
object x there:

- Insert the object x
into the R-tree:
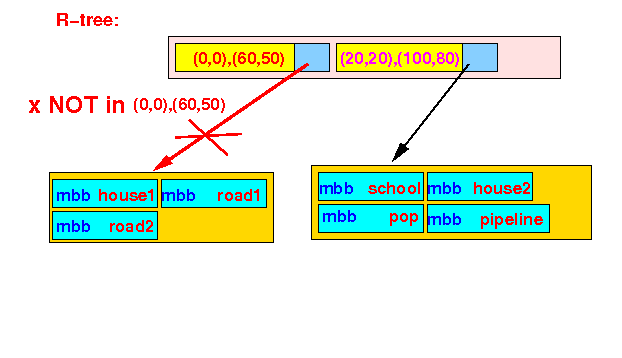
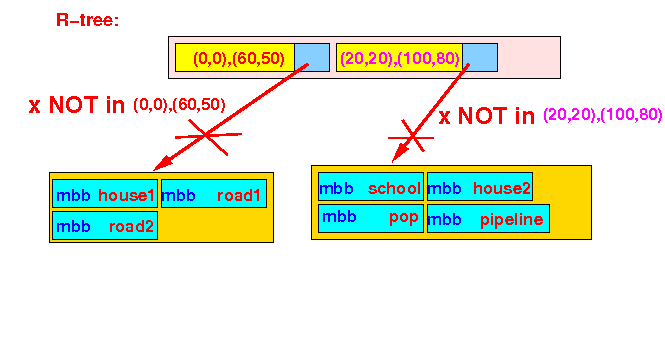
- Insert example 2:
(augmenting the
bounding box)
- Insert the object x
into the R-tree:
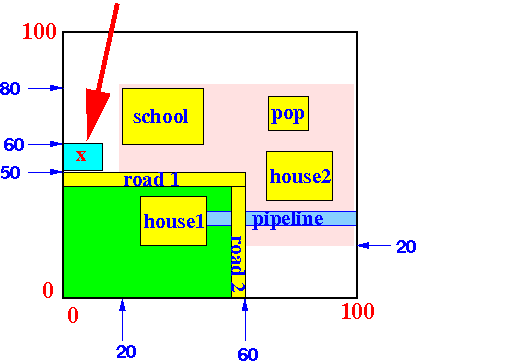
Steps of the Insert Algorithm:
- Find a
bounding box that contain
x:
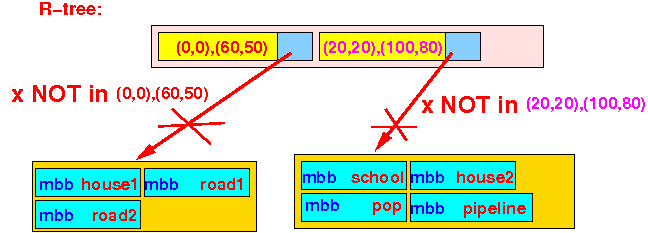
We cannot find any BB that contains the object x, therefore:
Augment one of the bounding boxes
- We can
augment
the first BB to:
( (0,0) , (60,60) )Graphically:
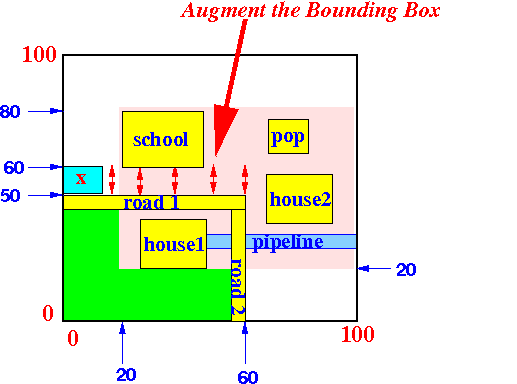
so that the new will include the object x:

Note:
- The fact that we are
searching in the
current node must mean:
- The BB in the parent node contains the object x !!!
- Therefore:
- There is no need to update the BB in the parent node !!!
- The fact that we are
searching in the
current node must mean:
- After augmenting,
we
can insert
the object x in the
subtree:
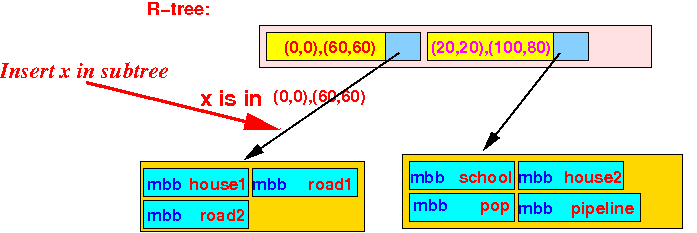
Which will insert x in this leaf node:
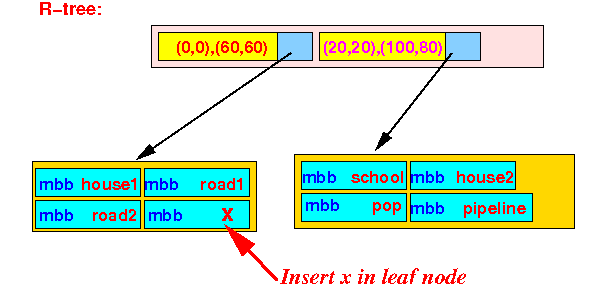
Which represents the following result:

- Insert the object x
into the R-tree:
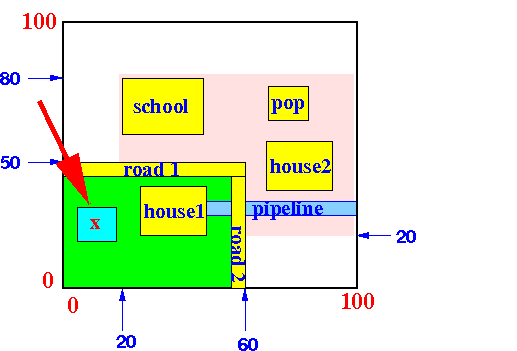
- Insert example 3:
(split a
leaf node)
- Insert the object x
into the R-tree:

Steps of the Insert Algorithm:
- We find a
BB that contains
the object x:
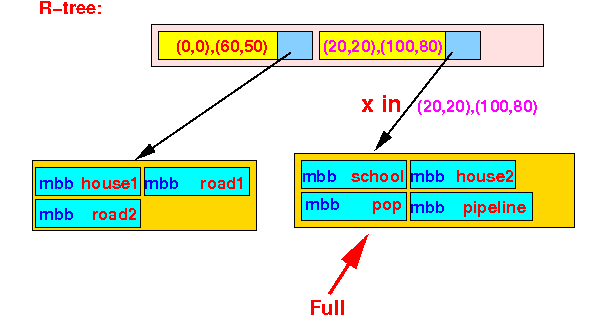
However, the leaf node is full:
- We partition the objects into 2 groups
- Suppose we partition
the objects as
follows:
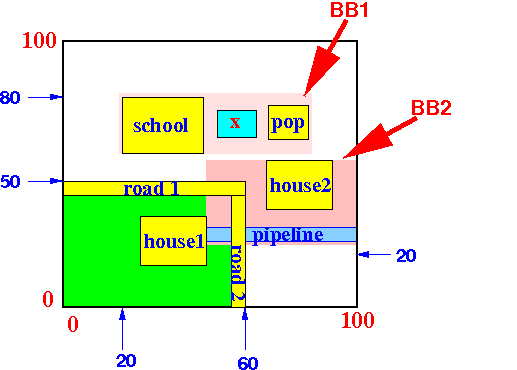
- The new
R-tree is then:

Notice that:
- The bounding box ( (20,20), 100,80) ) in the parent node is replaced by 2 bounding boxes BB1 and BB2
- Insert the object x
into the R-tree:
- Differences between
R-tree and
B-tree
insert algorithms:
- When you
insert a
new object (mbb, ObjID)
into the R-tree:
- During the search through the internal nodes of the R-tree, we may need to expand some BB in the search key to include (= contain) the mbb of the inserted object
See example 2 above:
- In order to insert the object
x into the
R-tree:

We need to augment one of the Bounding Boxes:

(You do not need to adjust the search key values in a B+-tree to accommodate a new search key)
- When a leaf node
overflows:
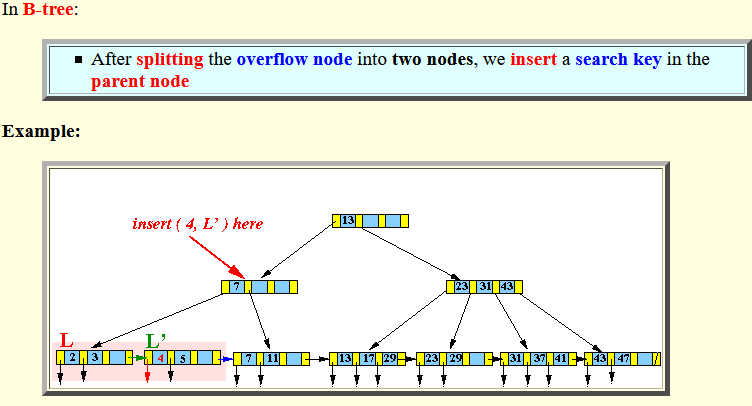
- In B-tree:
- After splitting the overflow node into two nodes, we insert a search key in the parent node
Example:
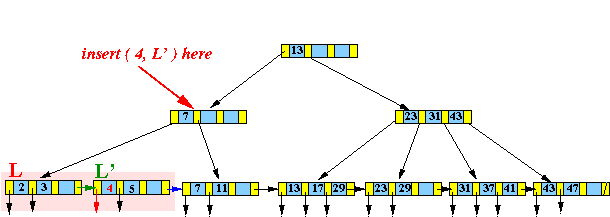
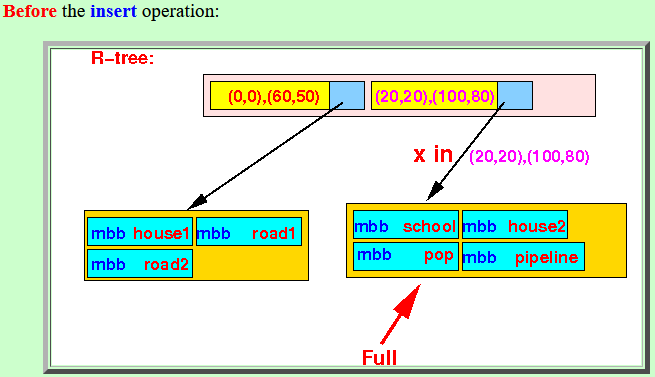
- In R-tree:
- After splitting the overflow node into two nodes, we replace a (search) bounding box in the parent node by two (2) new (search) bounding boxes
Example:
- Before the
insert operation:

- After the
insert operation:
- In B-tree:
- When you
insert a
new object (mbb, ObjID)
into the R-tree:
- Notice that:
- Inserting an
object can
trigger an
insertion
(of a search bounding box) in
an internal node:

One (search) bounding box is replaced by two (search) bounding boxes
- Inserting an
object can
trigger an
insertion
(of a search bounding box) in
an internal node:
- Fact:
- The insert algorithm for
an internal node is
similar to the
one used for
leaf node
(I will skip the insert algorithm for an internal node)
- The insert algorithm for
an internal node is
similar to the
one used for
leaf node
- However:
- There is a new problem that we must deal with in the R-tree when we split a node !!!!
Problem description:
- If the
internal node is
full:
- We must split (= re-distribute) the bounding boxes (= objects) stored in the node into 2 parts (and stored in 2 internal nodes)
Example:
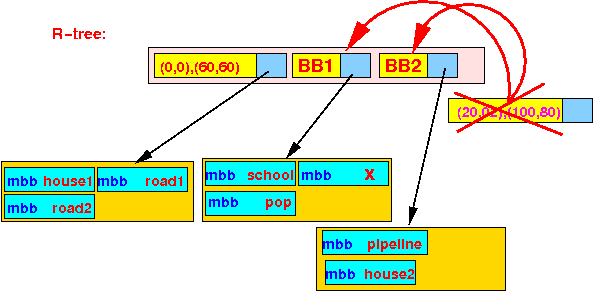
- Suppose the
root (internal) node can
only store
2 (search) bounding boxes:

- We must split (= re-distribute) the
bounding boxes into
2 groups:
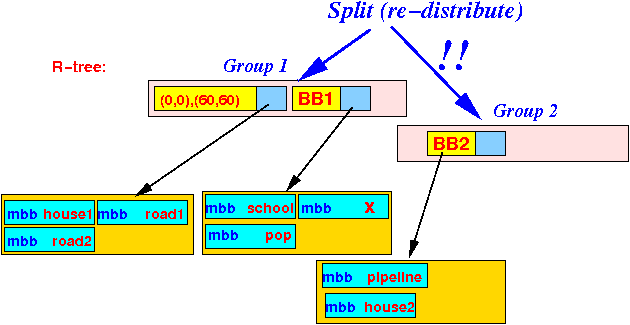
- 64,000 question:
- How should we
split the
(search) bounding boxes ????
Graphically:
- Should we re-distribute the
objects into
these 2 groups:

- Or:
should we re-distribute the
objects into
these 2 groups:

Etc. etc !!!
(The bounding boxes are not "sorted" like search keys in a B-tree !!!)
- Should we re-distribute the
objects into
these 2 groups:
- How should we
split the
(search) bounding boxes ????