Slideshow:
B+-tree insertion - example 1
Insert the search key 10
B+-tree insertion - example 1
Find the leaf node that will contain the search key (10)
B+-tree insertion - example 1
No overflow: done !
B+-tree insertion 2: full leaf node,
cascade insert up 1 level
Insert the search key 4
B+-tree insertion 2: full leaf node,
cascade insert up 1 level
Find the leaf node that will contain the search key 4
B+-tree insertion 2: full leaf node,
cascade insert up 1 level
Inserting the key 4 would cause overflow - I use a virtual node to simplify the split operation
B+-tree insertion 2: full leaf node,
cascade insert up 1 level
The overflow "virtual" node is split in two - the new disk block is R
B+-tree insertion 2: full leaf node,
cascade insert up 1 level
I redrawed the B+-tree with the old node (L) and the new node (R) - you can see that R is unlinked !
B+-tree insertion 2: full leaf node,
cascade insert up 1 level
The leaf insert algorithm calls InsertInternal(4, R, parent(L))
B+-tree insertion 2: full leaf node,
cascade insert up 1 level
The parent node has space (i.e.: no overflow) - done !
B+-tree insertion 3: full leaf node,
cascade insert up multiple levels
Insert the search key 40
B+-tree insertion 3: full leaf node,
cascade insert up multiple levels
Find the leaf node that will store the search key
B+-tree insertion 3: full leaf node,
cascade insert up multiple levels
The insertion creates a overflow virtual node that we must split in two (virtual node shown for clarity only)
B+-tree insertion 3: full leaf node,
cascade insert up multiple levels
The overflow node is split in two using a new node (disk block) R
B+-tree insertion 3: full leaf node,
cascade insert up multiple levels
I have redrawn the state of the algorithm to show you that node R is not linked to the B+-tree
B+-tree insertion 3: full leaf node,
cascade insert up multiple levels
The Insert( ) will call InsertInternal( (40,R), parent(L) ) !!
B+-tree insertion 3: full leaf node,
cascade insert up multiple levels
Inserting (40,L) into the full parent node will result in an overflow virtual node that we must split in two
B+-tree insertion 3: full leaf node,
cascade insert up multiple levels
The InsertInternal( ) function will split the overflow node in two
B+-tree insertion 3: full leaf node,
cascade insert up multiple levels
After the split, it will recursively call InsertInternal( (40, R), parent(oldNode) )
B+-tree insertion 3: full leaf node,
cascade insert up multiple levels
The call InsertInternal( (40, R), parent(oldNode) ) will insert(40, R)...
B+-tree insertion 3: full leaf node,
cascade insert up multiple levels
After insertion, there is no overflow: done !!
B+-tree insertion 4: split the root node
Insert the search key 15
B+-tree insertion 4: split the root node
Find the leaf node that will store the search key 15
B+-tree insertion 4: split the root node
Insertion will create a "overflowed" virtual node that we need to split
B+-tree insertion 4: split the root node
Split the search keys using a new node (disk block) R
B+-tree insertion 4: split the root node
I redraw the split nodes in the B+-tree. Notice the new node R is unlinked.
B+-tree insertion 4: split the root node
Insert( ) method will call InsertInternal((17, R), parent(L))
B+-tree insertion 4: split the root node
Inserting (17, R) in root node will create an overflowed virtual node that we need to split
B+-tree insertion 4: split the root node
The InsertInternal( ) will split the overflow node.
B+-tree insertion 4: split the root node
After the split, it will insert (31, R) in the node parent(L). However: L is the root node
B+-tree insertion 4: split the root node
If L was the root node, we create a new root node: done !
- Insert
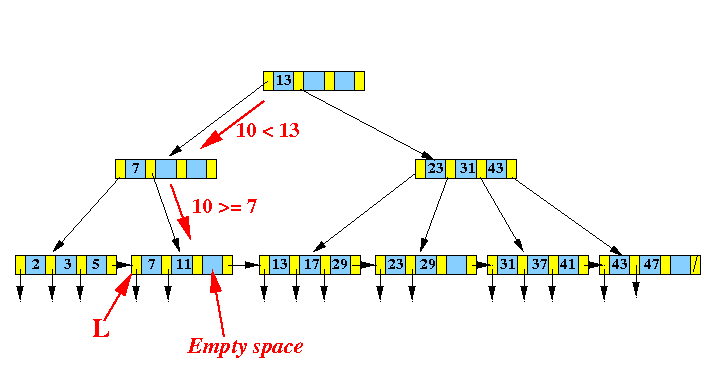
( 10, recordPtr(10) ) into
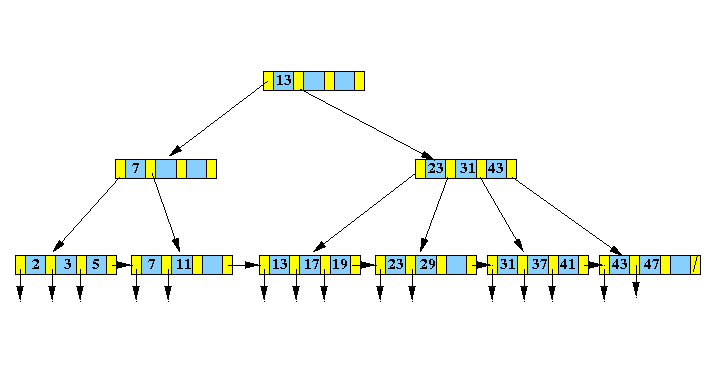
the following
B+-tree:
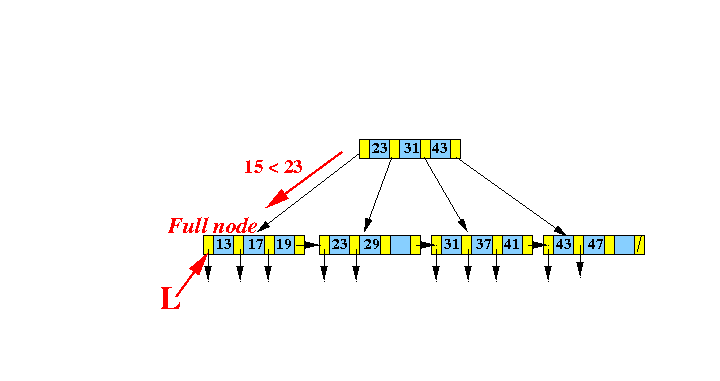
- Insert Algorithm:
- Find the
leaf node L that would
contain
search key
10:
- Shift keys and
insert
( 10, recordPtr(10) )
into the correct position:
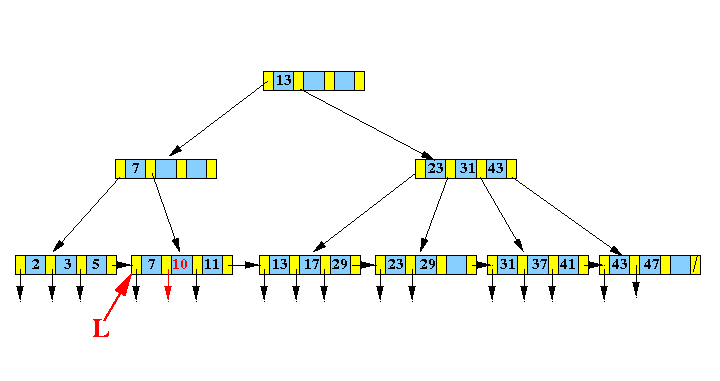
- Find the
leaf node L that would
contain
search key
10:
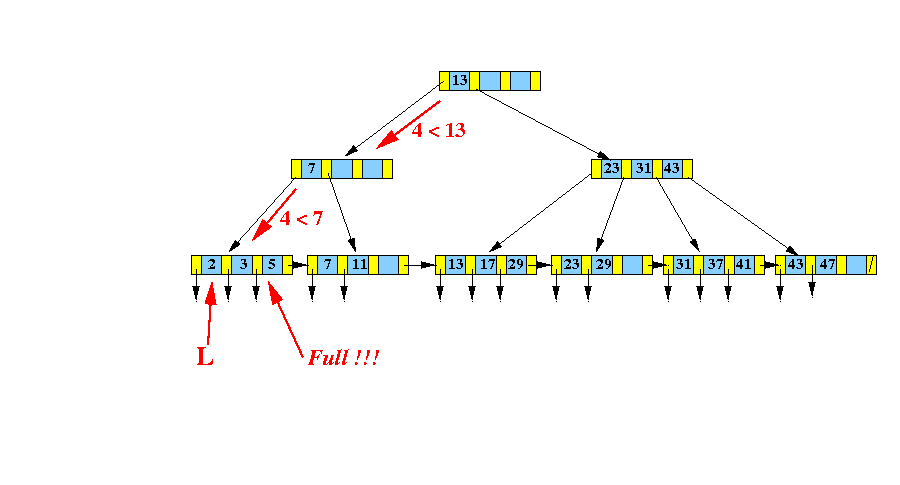
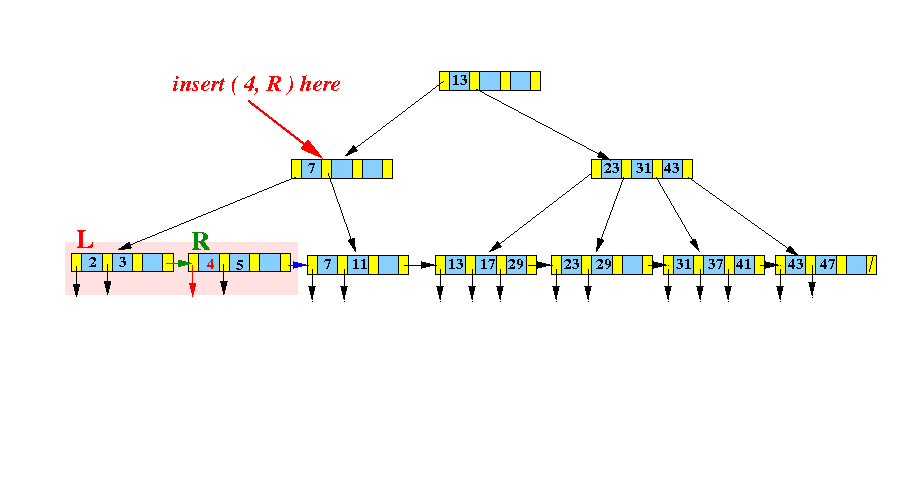
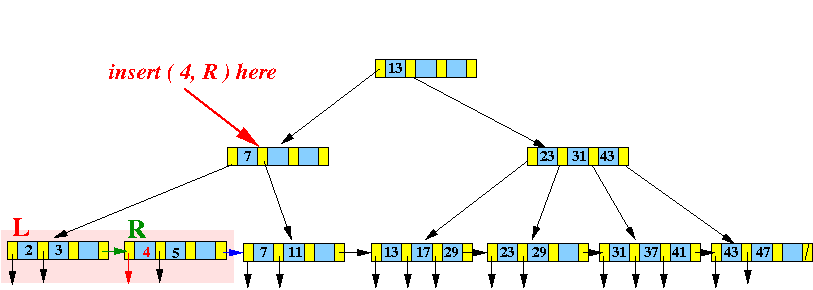
- Insert
( 4, recordPtr(4) ) into
the following
B+-tree:
- Leaf Insert Algorithm:
- Find the
leaf node L that would
contain
search key
4:
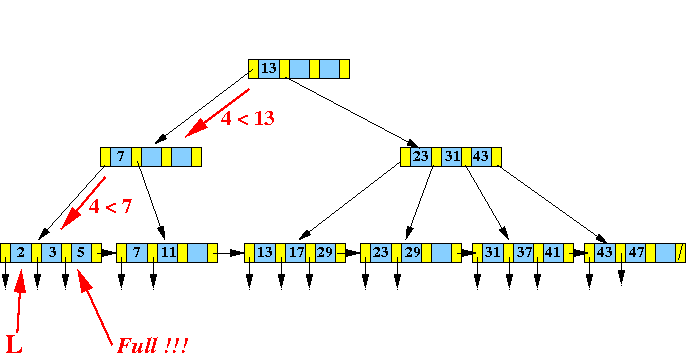
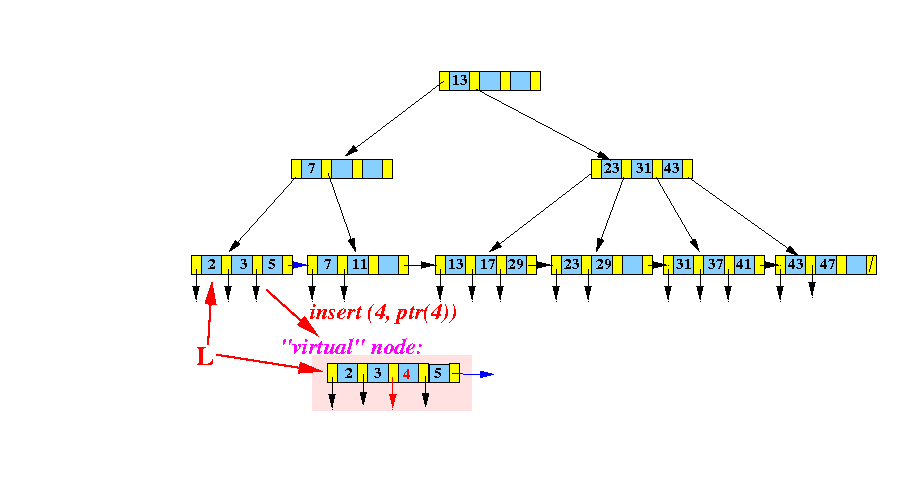
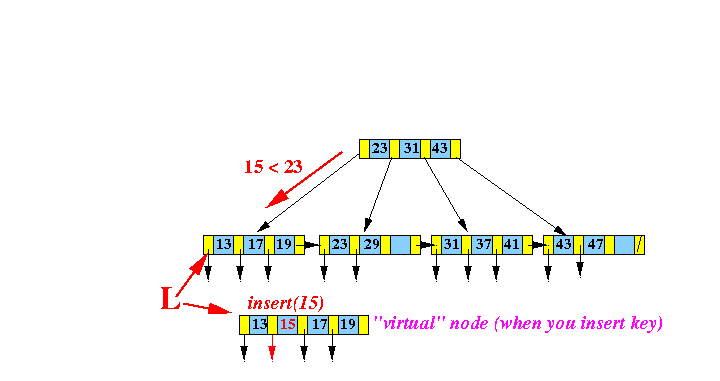
- Make a virtual node
by
inserting
( 4, recordPtr(4) )
into the correct position:
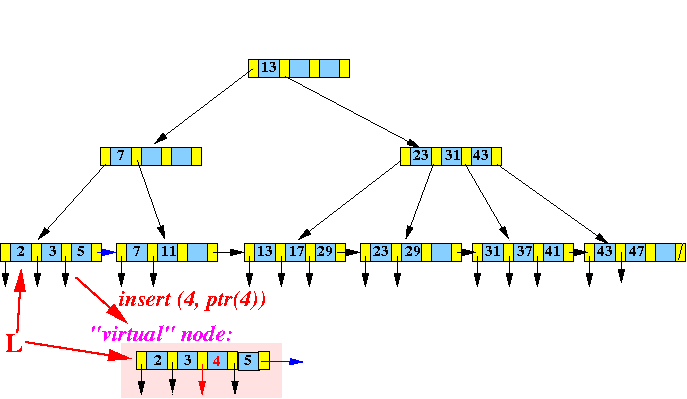
(The virtual node does not exist !
This step is only done to help you visualize the insert algorithm)
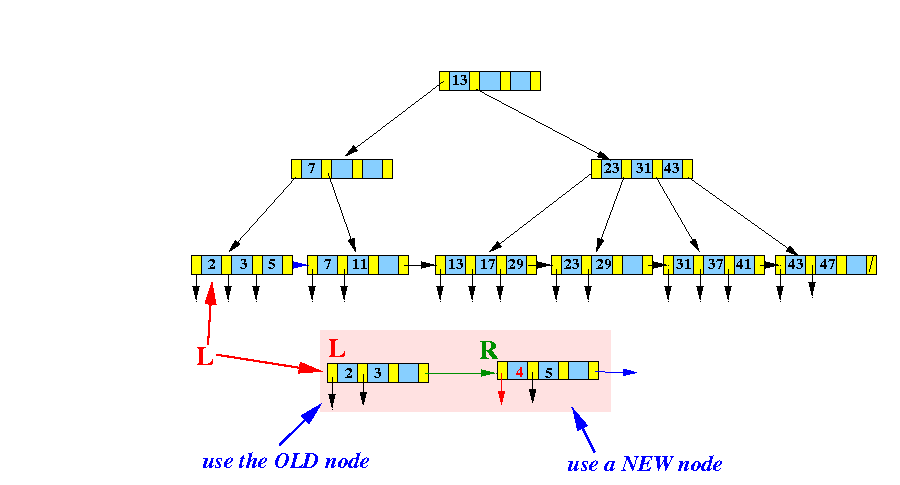
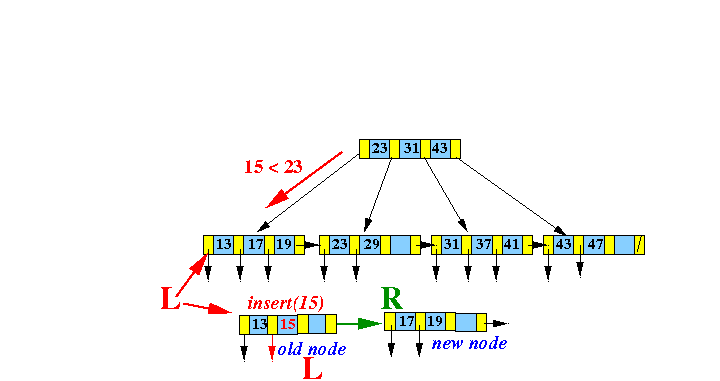
- Split this
virtual node into
2 "equal" halves:
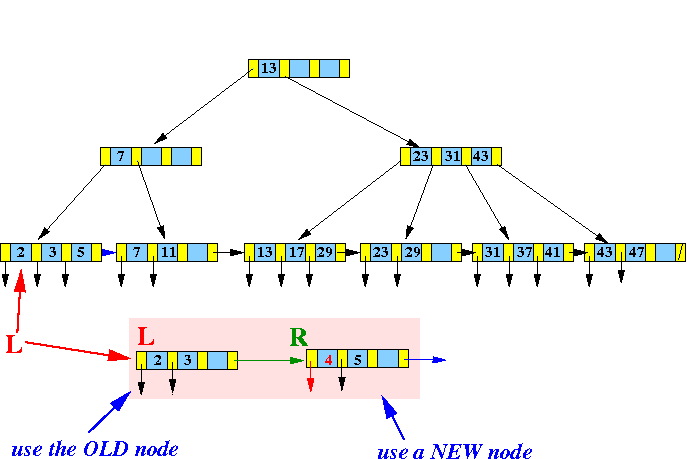
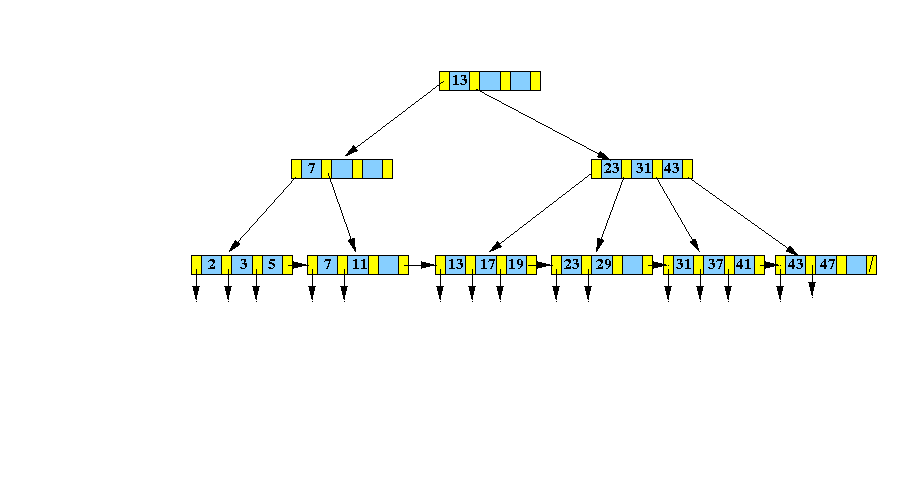
Redrawn:
Next:
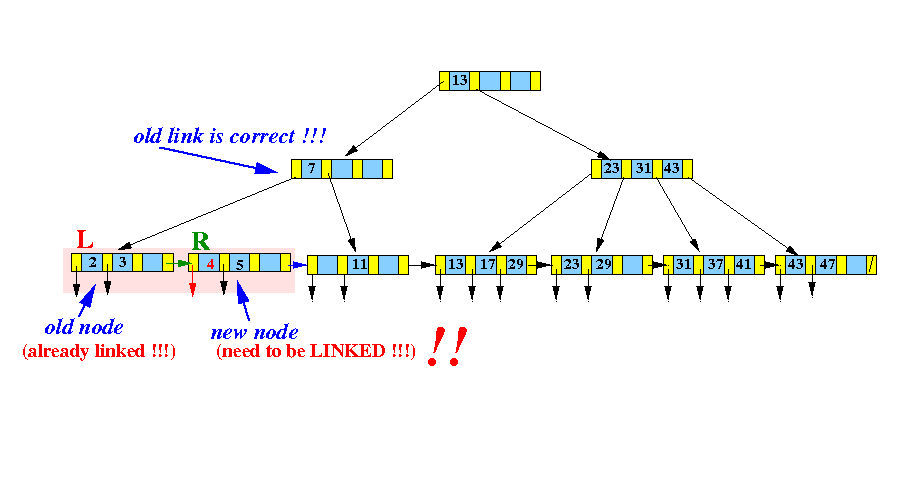
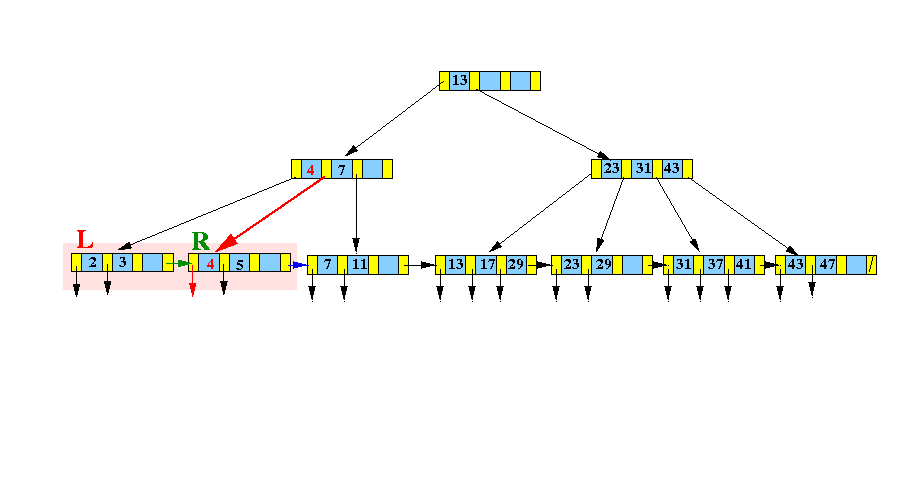
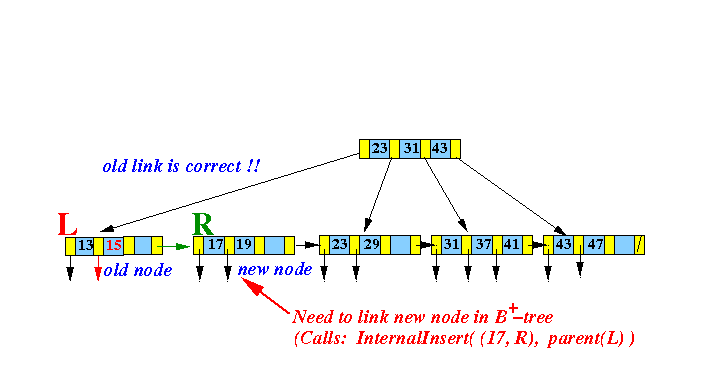
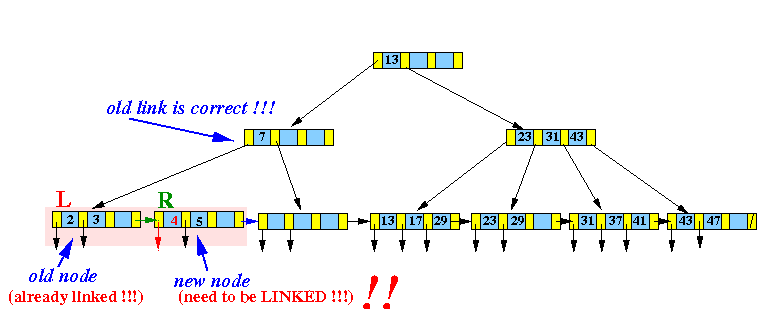
- Use
InsertInternal( ) to
insert:
- The middle search key (= 4) (and the new node pointer R) --- (4, R) --- into the parent node of L
Graphically:
- Use
InsertInternal( ) to
insert:
- Find the
leaf node L that would
contain
search key
4:
- Continue with
the
InsertInternal( (4,R), parent(L) ) algorithm:
-
Insert
(4, R) into the
parent node of
L:
Result:
Notice that the node R is the right subtree of the key 4 !!!
DONE !!!
-
Insert
(4, R) into the
parent node of
L:
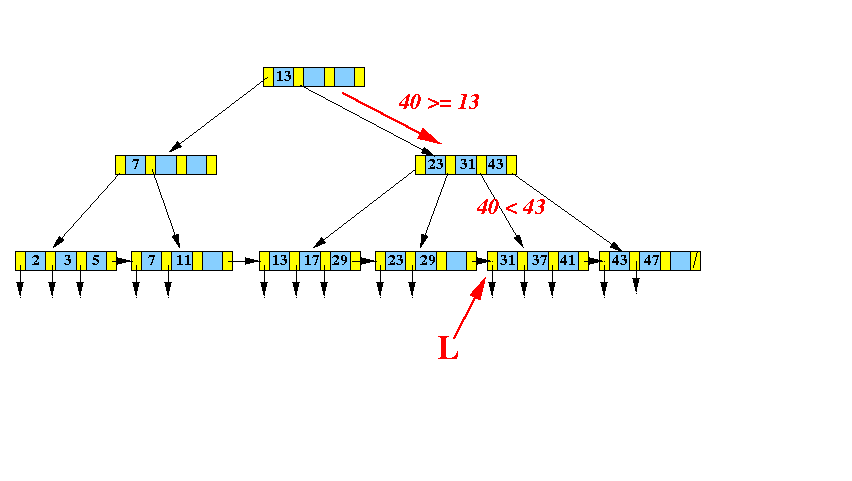
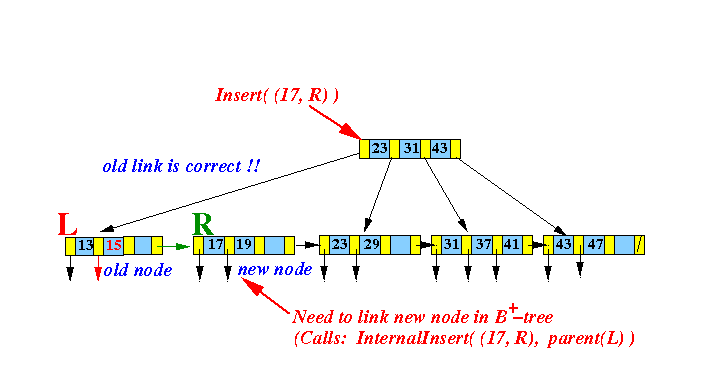
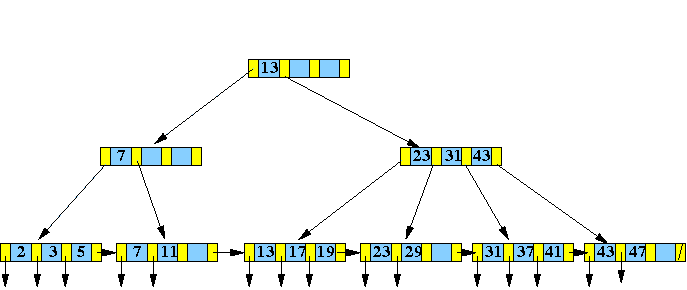
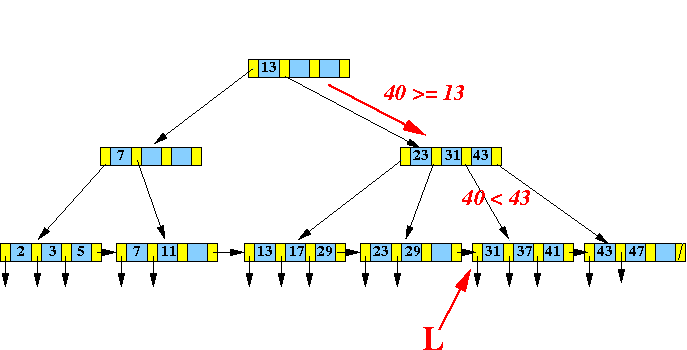
- Insert
( 40, recordPtr(40) ) into
the following
B+-tree:
- Insert Algorithm:
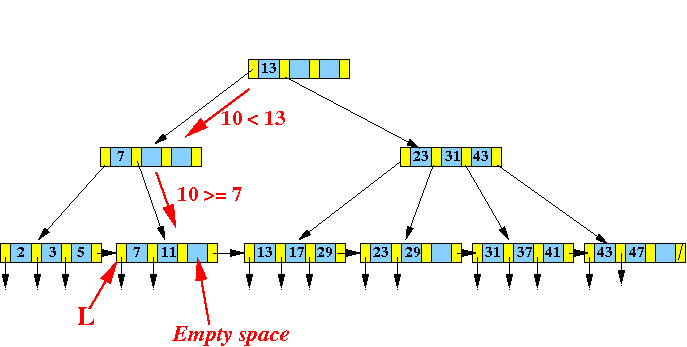
- Find the
leaf node L that would
contain
search key
40:
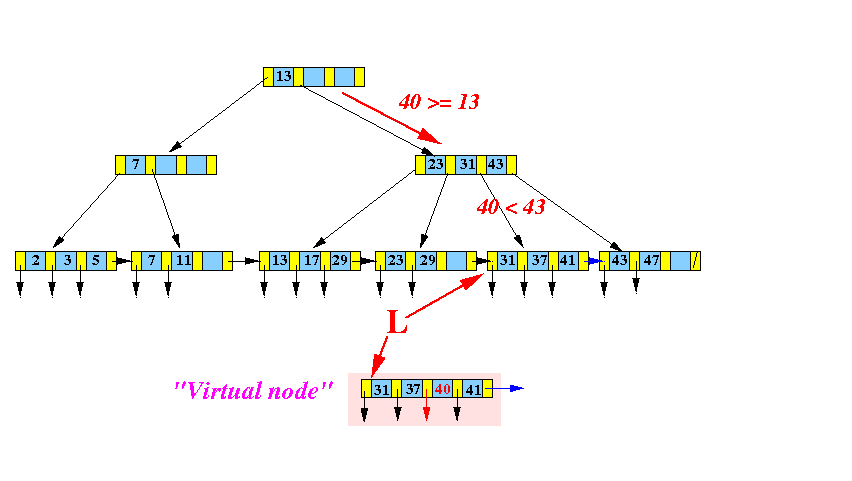
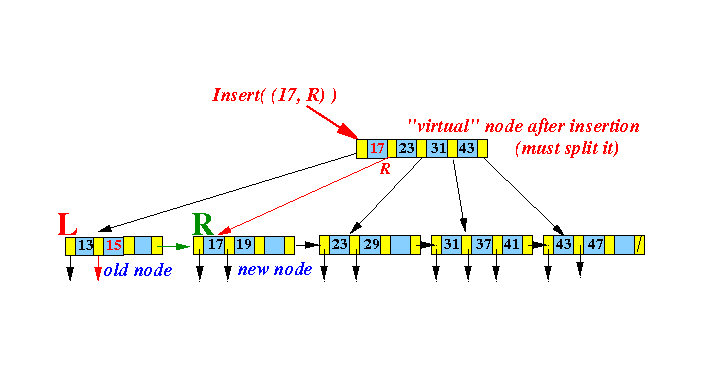
- Make a virtual node
by
inserting
( 40, recordPtr(40) )
into the correct position:
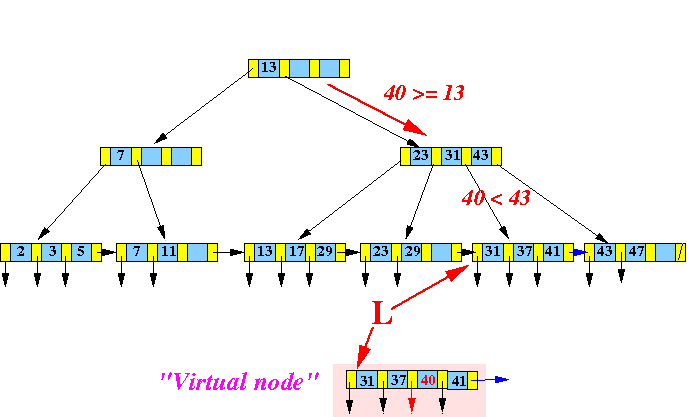
(The virtual node does not exist !!!!!
This step is only done to help you visualize the insert algorithm)
- Split this
virtual node into
2 "equal" halves:
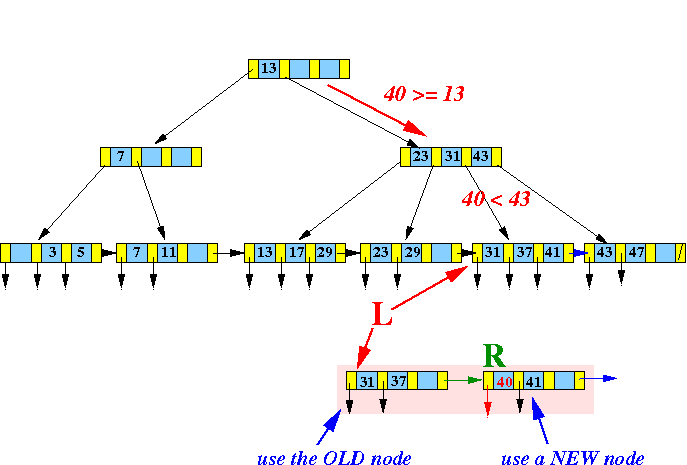
Redrawn:
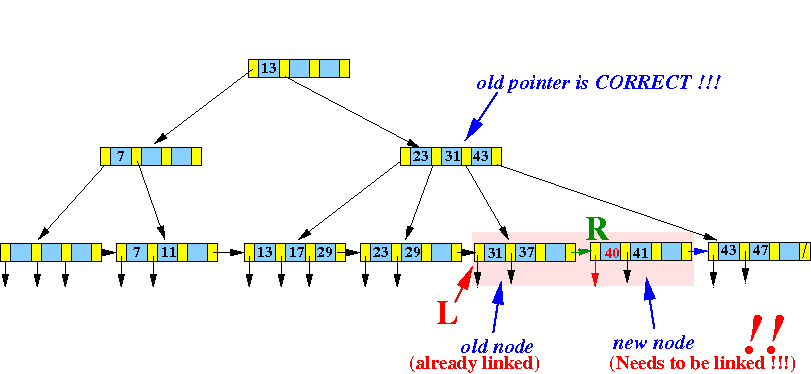
Next:
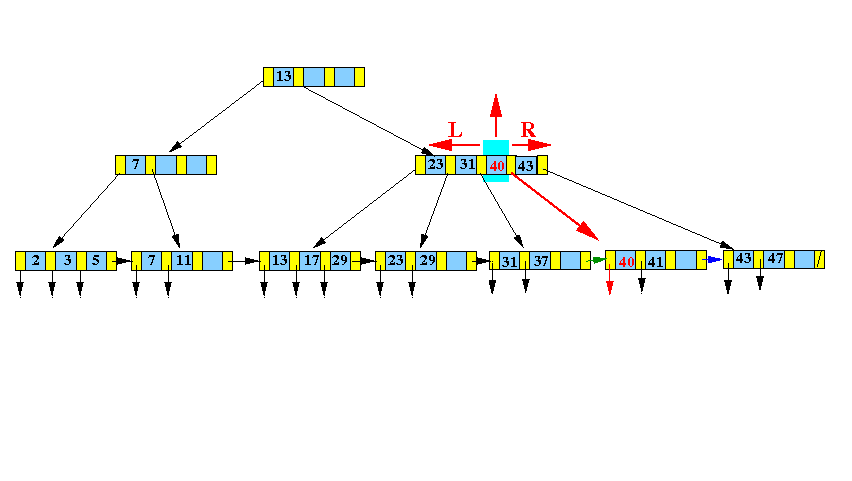
- Use InsertInternal( ) to insert (40, R) into the parent node of L
Graphically:
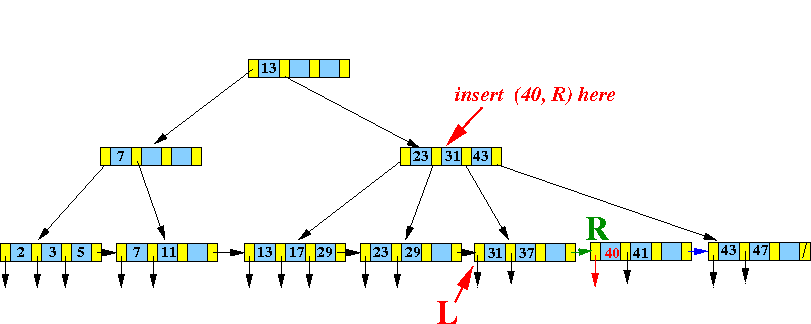
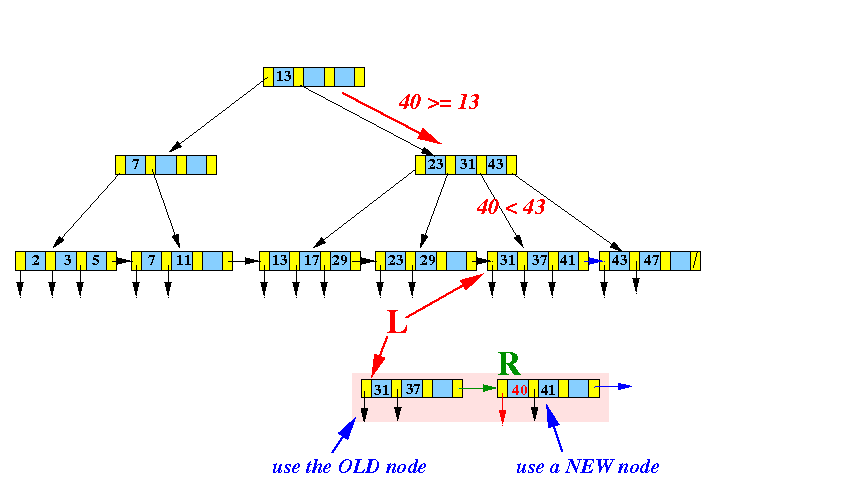
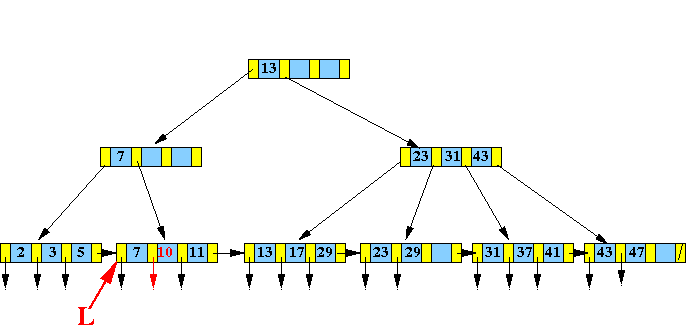
- Find the
leaf node L that would
contain
search key
40:
- Continue with the
InsertInternal( (40,R), parent(L) )
algorithm:
-
Insert
(40, R) into the
parent node of
L:
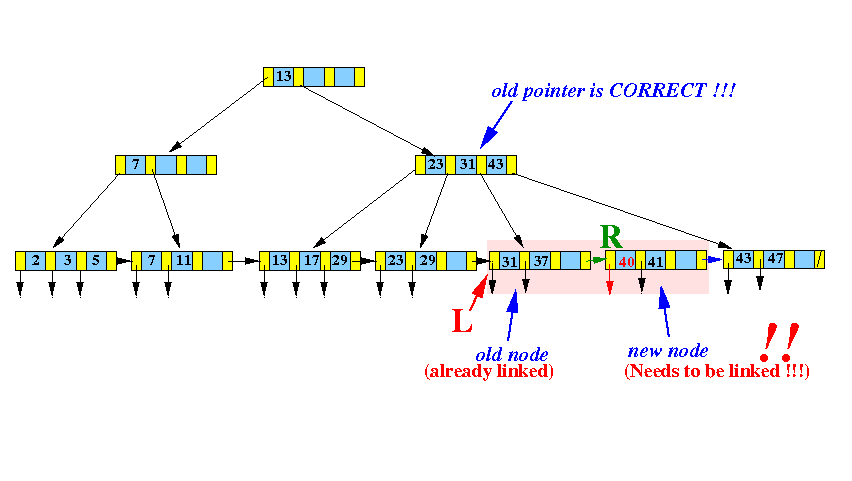
Result:
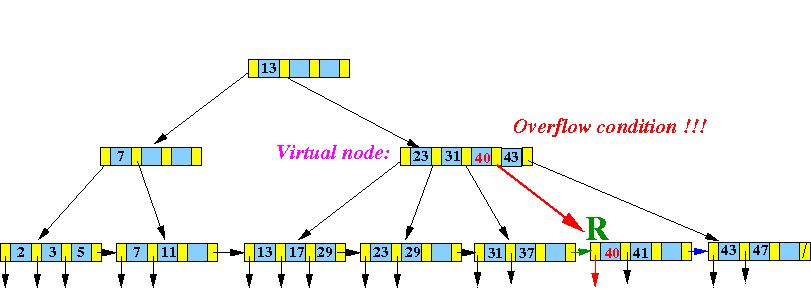
(The virtual node does not exist !!!!! Shown here to make algorithm more concrete)
This step is only done to help you visualize the insert algorithm
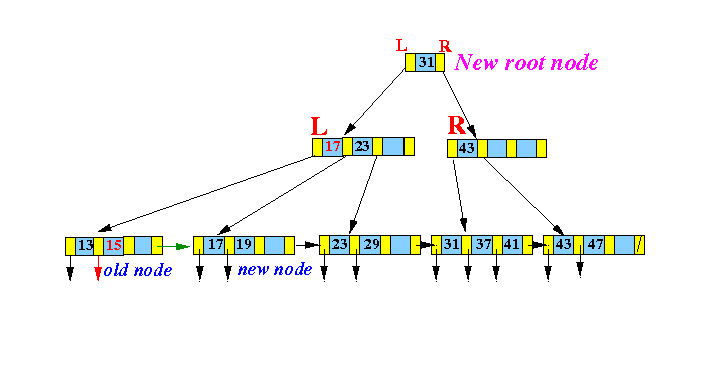
BTW: I will re-use the letters L and R for the next level of node split --- the letters L and R now denote different nodes !!!
-
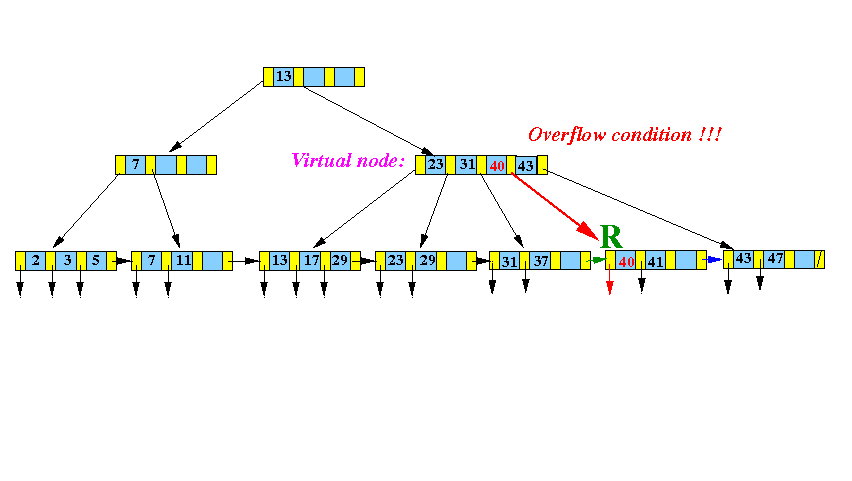
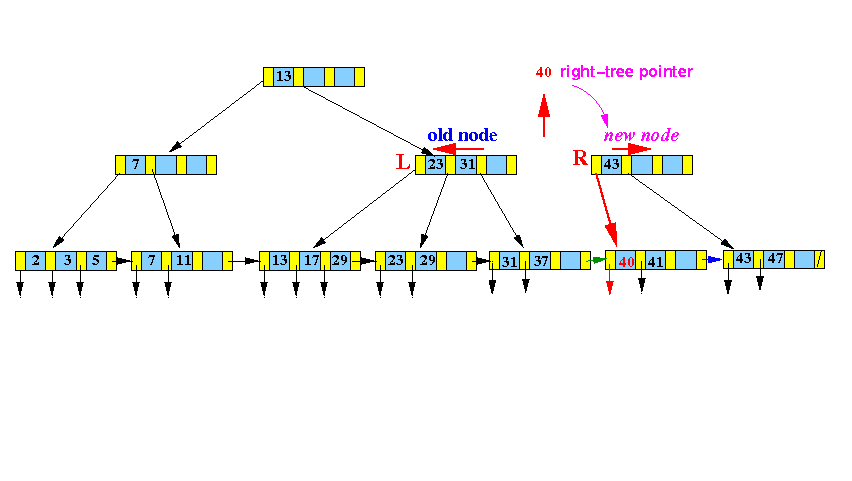
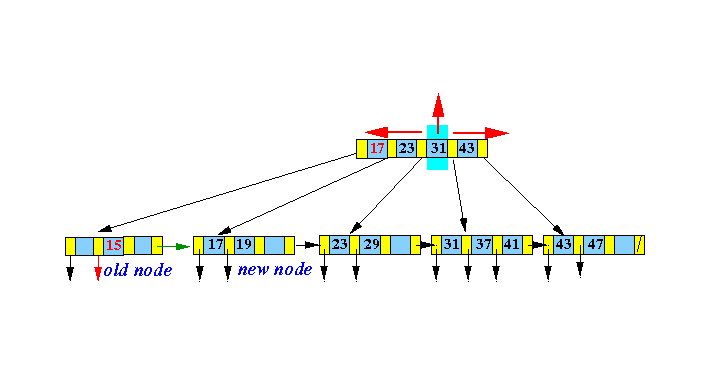
Split this
virtual node
into
3 parts:
- Take the middle node out !!!
- Make a left half node L
- Make a right half node R
Graphically:
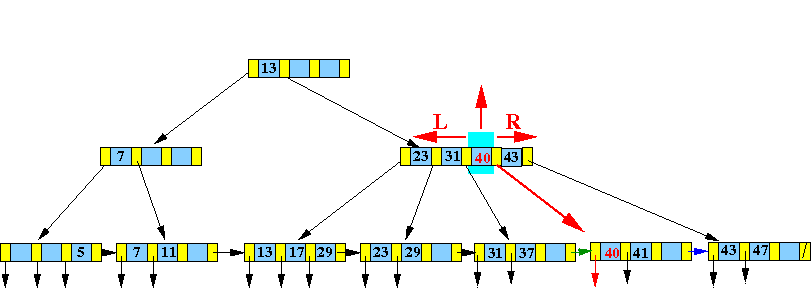
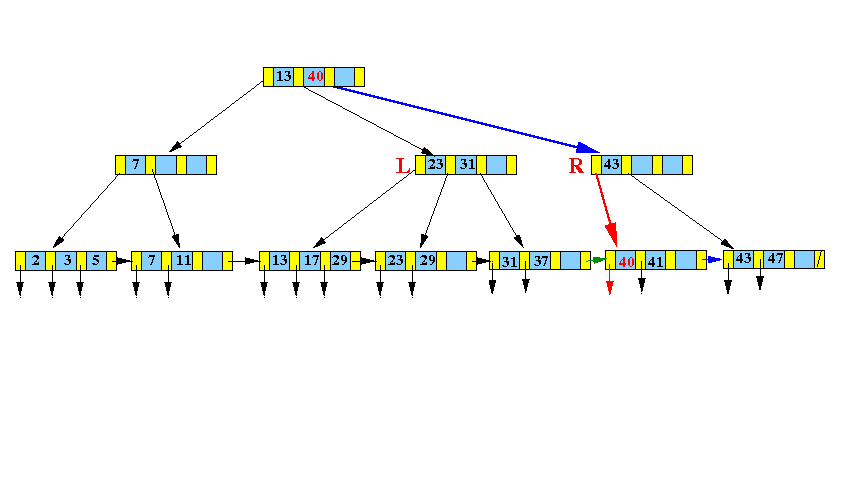
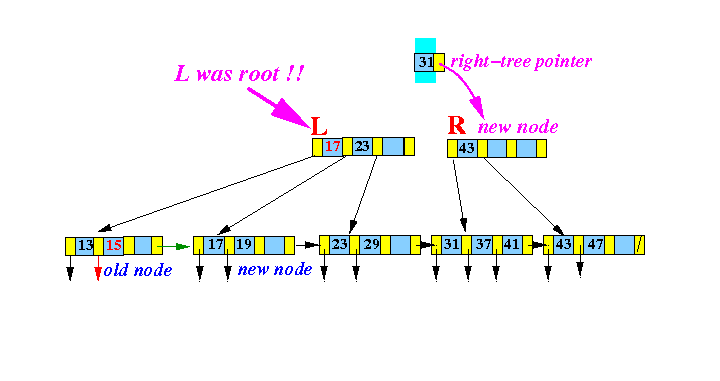
Result:
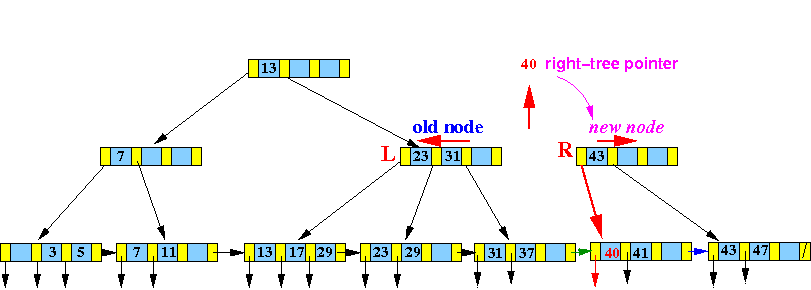
Notice that the new node R is the right subtree of the key 40 !!!
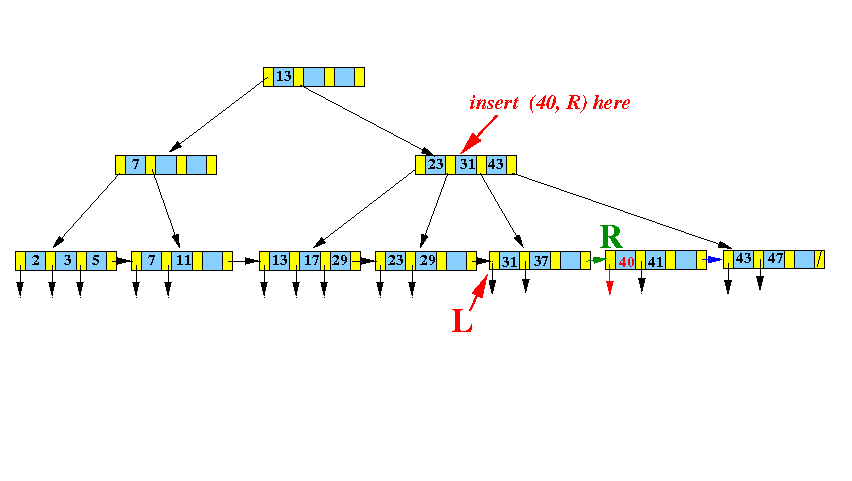
Recurse:
InsertInternal( (40, R), parent(L) )
- InsertInternal( (40, R), parent(L) ):
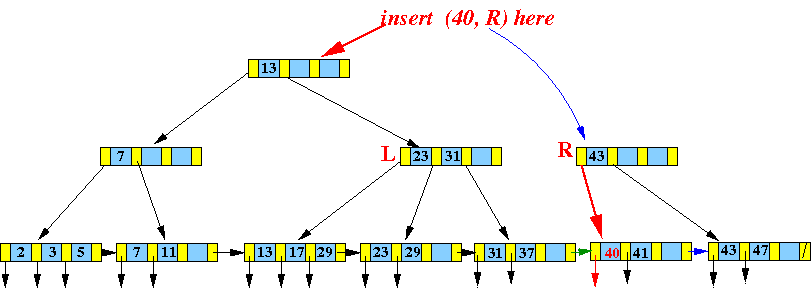
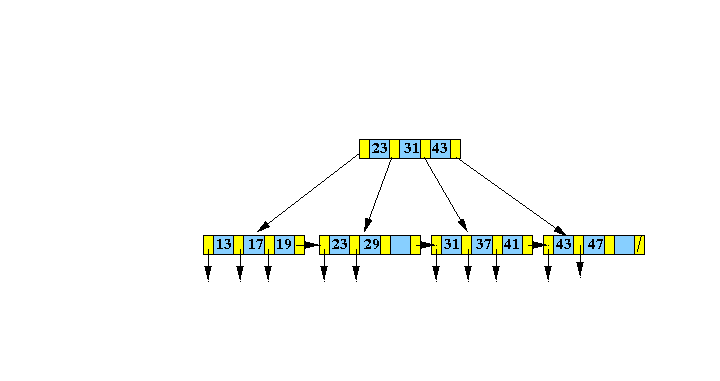
Result:
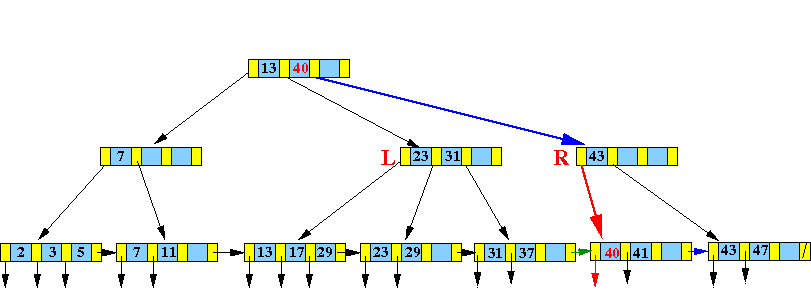
DONE !!!
-
Insert
(40, R) into the
parent node of
L: