- Recall:
- The index file is used to speed up the look up records in a data file using a search key
- Therefore:
- When we insert a
new record in
the data file:
- We must also insert the search key of the new record into the index file (in our case: the B+-tree)
- When we delete a
record from
the data file:
- We must also delete the search key of the deleted record into the index file (in our case: the B+-tree)
- When we insert a
new record in
the data file:
- Index file:
- Index file =
a file that store
records of the
following format:
+------------+----------------------+ | Search key | block/record pointer | +------------+----------------------+Graphically:
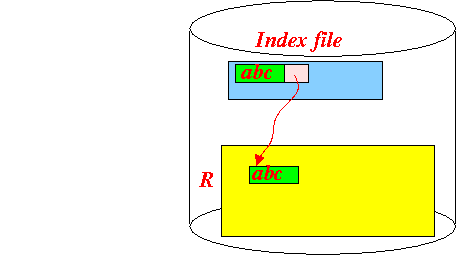
- Index file =
a file that store
records of the
following format:
- Therefore:
- In an insert operation,
we will always insert
a (key, record-address) pair
in the B+-tree
- In an delete operation, we will always insert a (key, record-address) pair from the B+-tree
- In an insert operation,
we will always insert
a (key, record-address) pair
in the B+-tree
- Assumption:
- We assume the search keys
in the B-tree are
unique
I.e.: no duplicate keys stored in the B-tree
- We assume the search keys
in the B-tree are
unique
- Overview of the
B-tree
insert
algorithm:
- A (new) search key
(and a corresponding
record pointer) is
(always) inserted into a
leaf node
- The insertion can cause an overflow condition which will split the leaf node into 2 leaf nodes
- An overflow condition
will trigger the
execution
of the
insert algorithm for
an internal node
- The
insert algorithm for
an internal node is
similar
(but is not the same) as
the
insert algorithm for
a leaf node !!!
(So we will actually discuss 2 insertion algorithms !!!)
- The
insert algorithm for
an internal node is
similar
(but is not the same) as
the
insert algorithm for
a leaf node !!!
- A (new) search key
(and a corresponding
record pointer) is
(always) inserted into a
leaf node
- Middle key:
- Let n =
the number of
keys in a
B+ tree node
The middle key is the key with the index equal to:
m = ⌈ (n+1)/2 ⌉
- Examples: the middle key
n | m ---------+-------- 3 | 2 1 2 3 4 | 3 1 2 3 4 5 | 3 1 2 3 4 5 6 | 4 1 2 3 4 5 6 ... | ...
Important note:
- When a node is
split (see below),
the node is
split at the
middle node
- The new right node will contain the middle key plus all the keys that follows the middle key
- Let n =
the number of
keys in a
B+ tree node
- Note:
- We
start
counting
keys at the
number
1:
- First key = p1
- Second key = p2
- Third key = p3
- ...
(Normally, computer science starts counting at 0 !!! :))
- We
start
counting
keys at the
number
1:
- Given:
- A B+-tree
- Search key value x
- Block/record pointer of x
Goal:
- Insert (x, ptr(x)) into the B+-tree
- A B+-tree
- Algorithm to
insert
( search key x, ptr(x) )
into a B+-tree:
/* ======================================================== Insert( x, record ptr(x) ) into B+-tree ======================================================== */ Insert( x, px ) { Use the B-tree search algorithm to find the leaf node L where the x belongs Let: L = leaf node used to insert x, px /* ============================================ Insert x, px in leaf node L ============================================ */ if ( L ≠ full ) { Shift keys to make room for x Insert (x, px) into its position in leaf node L return // Done } else // Overflow condition { /* ------------------------------------------- Leaf node L has n keys + n ptrs (= full !!!): L: |p1|k1|p2|k2|....|pn|kn|next| ------------------------------------------- */ Make the following virtual node by inserting px,x in L: |p1|k1|p2|k2|...|px|x|...|pn|kn|next| (There are (n+1) keys in this node !!!) Split this node in two 2 "equal" halves: Let: m = ⌈(n+1)/2⌉ L: |p1|k1|p2|k2|...|pm-1|km-1|R| <--- use the old node for L R: |pm|km|....|px|x|...|pn|kn|next| <--- use a new node for R /* ================================================== We need to fix the information at 1 level up to direct the search to the new node R We know that all keys in R: >= km ================================================== */ if ( L == root node of B+ tree ) { Make a new root node containing (L, km, R) return; } else { /* --------------------------------------------- Use the InsertInternal alg to insert: (km,R) into the parent node of L ---------------------------------------------- */ InsertInternal( (km, R), parent(L) ); // Note: all keys in R are ≥ km // So: R is the right subtree of km } } }