- Assumption:
- We assume the search keys in the B-tree are unique I.e.: no duplicate keys stored in the B-tree
- Recall:
- The
leaf nodes of a
B+-tree contains
the
(actual) index file:
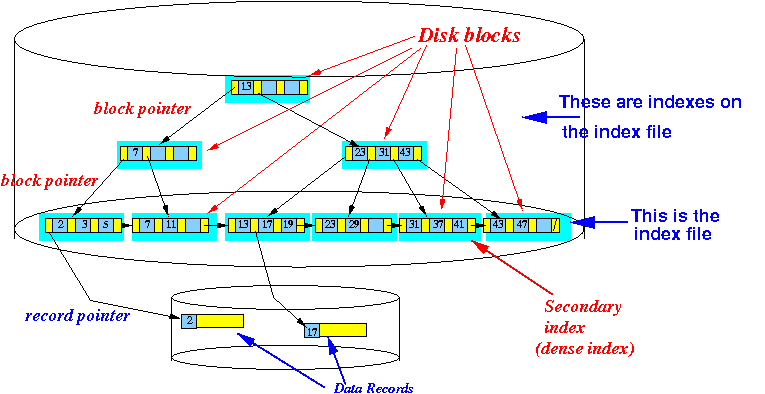
- Nodes in a B+-tree must satisfy a occupancy requirement !!!
- The
leaf nodes of a
B+-tree contains
the
(actual) index file:
- Deleting
from a node in a
B+-tree:
- Deletion from
a node can
cause a
violation of
the occupancy requirement !!!
- This condition is called underflow condition
- Deletion from
a node can
cause a
violation of
the occupancy requirement !!!
- Pre-requisite to
fixing the
underflow condition:
- Remember that:
- Each node is
- half full ≤ filled < full
- Each node is
Fixing the underflow condition:
-
First, we try
transfering a
key + pointer into
the underflowed node
- If a
transfer is
not possible then:
- We
merge the
underflowed node with
one of its
sibling nodes
This mereg operation will be guaranteed to succeed because the sibling node will be exactly half filled
- We
merge the
underflowed node with
one of its
sibling nodes
- Remember that:
- Given:
- A B+-tree
- Search key value x
Goal:
- Delete search key x and its (corresponding) record pointer from the B+-tree
- A B+-tree
- Delete Algorithm
for B+-tree:
/* ============================================================== Delete( x ) from B+-tree Input: search key x that we wish to delete from B+-tree index ============================================================== */ Delete( search key x ) // Algorithm will also delete the record pointer for x { Use the B-tree search algorithm to find the leaf node D where the x belongs if ( x not found in D ) { return; // Done. We can't delete a non-existing search key } else { Shift keys to delete the key x and its record ptr from the node } /* ============================================== We delete a search key (+ record ptr) from D ===> Node D may become underflow !!! Check and handle underflow condition ============================================== */ if ( D has ≥ ⌈n/2⌉ keys /* Node is at least half full*/ ) { return; // No underflow, done } else { /* --------------------------------------------------------- D underflowed: fix the size of D with transfer or merge --------------------------------------------------------- */ if ( leftSibling(D) has ≥ ⌈n/2⌉ + 1 keys ) { 1. transfer last key and ptr from leftSibling(D) into D; 2. update the search key in the parent node;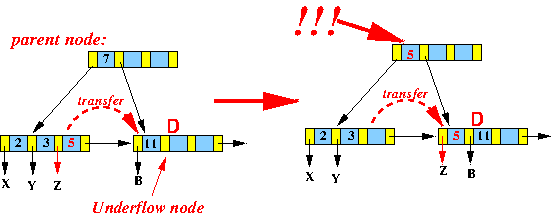 }
else if ( rightSibling(D) has ≥ ⌈n/2⌉ + 1 keys )
{
1. transfer first key and ptr from rightSibling(D) into D;
2. update the search key in the parent node;
}
else if ( rightSibling(D) has ≥ ⌈n/2⌉ + 1 keys )
{
1. transfer first key and ptr from rightSibling(D) into D;
2. update the search key in the parent node;
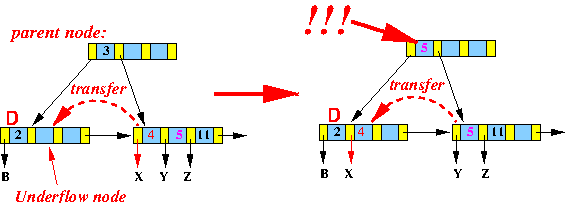 }
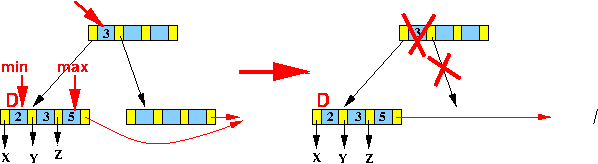
else if ( leftSibling(L) exists ) // Siblings are min nodes
{
1. Merge leftSibling(D) + D + D's last pointer
into leftSibling(D); // Node D will be deleted !!
}
else if ( leftSibling(L) exists ) // Siblings are min nodes
{
1. Merge leftSibling(D) + D + D's last pointer
into leftSibling(D); // Node D will be deleted !!
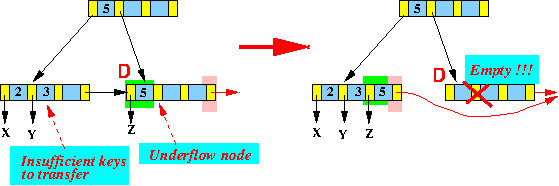 2. Find key x in parent(leftSib(D)) such that:
minKey(leftSib(D)) < x ≤ maxKey(leftSib(D))
DeleteInternal( x, rightTreePtr(x), parent(leftSib(D));
= Delete key and right subtree in parent node; // discuss next !!
2. Find key x in parent(leftSib(D)) such that:
minKey(leftSib(D)) < x ≤ maxKey(leftSib(D))
DeleteInternal( x, rightTreePtr(x), parent(leftSib(D));
= Delete key and right subtree in parent node; // discuss next !!
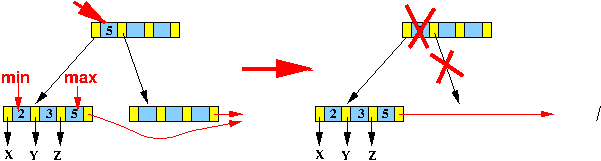 }
else
{
1. Merge: D + rightSibling(D) + rightSibling(D)'s last pointer
into the node D; // The rightSibling(D) node will be deleted !!!
}
else
{
1. Merge: D + rightSibling(D) + rightSibling(D)'s last pointer
into the node D; // The rightSibling(D) node will be deleted !!!
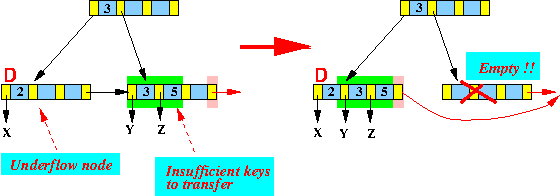 2. Find key x in parent(D) such that:
minKey(D) < x ≤ maxKey(D)
DeleteInternal( x, rightTreePtr(x), parent(leftSib(D));
= Delete key and right subtree ptr in parent node; // discuss next !!
2. Find key x in parent(D) such that:
minKey(D) < x ≤ maxKey(D)
DeleteInternal( x, rightTreePtr(x), parent(leftSib(D));
= Delete key and right subtree ptr in parent node; // discuss next !!
 }
}
}
}
Notice that:
- The delete operation
will trigger:
- A deletion of the key x and its right subtree pointer from an internal node
- The delete procedure
in an
internal node
is similar to
the delete procedure
in a
leaf node
But differs in a few minor details.... --- discussed next !!!
- The delete operation
will trigger: