---

A sufficient condition for a lossless decomposition

---

• A sufficient condition for content(R₁) * content(R₂) = content(R)
  • Lemma 2

    Let R1 and R2 be a decomposition of R If either   R1 ∩ R2 → R1   or   R1 ∩ R2 → R2 , then: content(R) = content(R1) * content(R2)

    ---

  • Proof:

    Omitted for brevity.....

    ---

    ---

  • Comment:

    I am using the lemma numbering from the text book.... In the text book, the above lemma is Lemma 2 (because I skipped some theory stuff to cover the material in a more speedy fashion)

  ---

  ---

  ---

  ---

• How to apply the lemma
  • Suppose the following functional dependency in relation R causes a violation of the 3NF property:

    A → B

    (I.e.: (1) A is not a super key   and   (2) B is not part of a key)

    Then you can decompose (= break up) the relation R into the following 2 relations R₁ and R₂ losslessly:

    ---

    ---

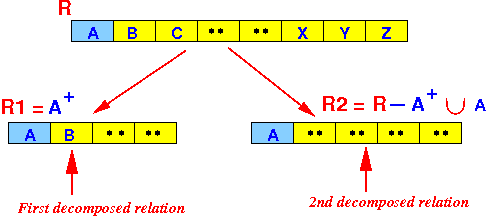
  • Reason:

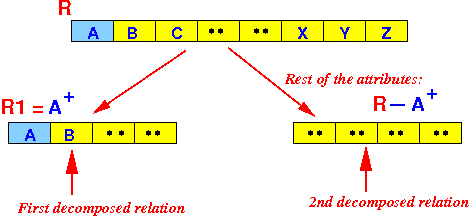
    Because the functional dependency: A → B you must take out (= break up) all attributes that is functionally dependent of A (the left hand size of the "problem" functional dependency): So the initial decomposition is: R1 = relation that contains all attributes in A+ R2 = relation that contains all attributes in R − A+ However: This initial decomposition is not guaranteed to be a lossless decomposition !!!       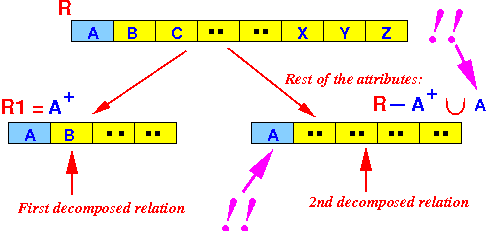According to Lemma 2, if we add the attribute A to the 2nd decomposed relation (R − A+): The decomposition will be lossless because: R1 ∩ R2 = A and: A → R1 Therfore: Since R1 ∩ R2 → R1, by Lemma 2, this decomposition is lossless !!!

  ---

  ---

  ---

  ---

• Example using Lemma 2
  • Recall:

    Employee1(SSN, FName, LName, PNumber, PName, Hours) Functional dependencies: SSN → FName, LName PNumber → PName SSN, PNumber → Hours The key of Employee1 is: (SSN, PNumber)

    ---

  • We found a violation to the 3rd Normal Form (i.e., a "bad" functional dependency):

    SSN → FName, LName Because: (1) SSN is not a superkey and (2) FName, LName is not part of a key

    Applying Lemma 2, the following decomposition will be lossless:

    Employee1(SSN, FName, LName, PNumber, PName, Hours) SSN+ = (SSN, Fname, LName) We can losslessly decompose (= brake up) Employee1 into: R1 (SSN, FName, LName) R2 (SSN, PNumber, PName, Hours) (because R1 ∩ R2 = {SSN} → R1 !!!)

    ---

    ---

    ---

  • Example:
    Original relation: Employee1

    SSN	FName	LName	PNumber	PName	Hours
    111-11-1111	John	Smith	pj1	DBApplet	20
    111-11-1111	John	Smith	pj2	WebServer	10
    111-22-3333	Jane	Doe	pj1	DBApplet	5

    Decomposition:

    R1 SSN FName LName 111-11-1111 John Smith 111-22-3333 Jane Doe

    R2 SSN PNumber PName Hours 111-11-1111 pj1 DBApplet 20 111-11-1111 pj2 WebServer 10 111-22-3333 pj1 DBApplet 5

    ---

    ---

  • Reconstruction: (using the decomposed relations)

    R1 SSN FName LName 111-11-1111 John Smith 111-22-3333 Jane Doe

    *

    R2 SSN PNumber PName Hours 111-11-1111 pj1 DBApplet 20 111-11-1111 pj2 WebServer 10 111-22-3333 pj1 DBApplet 5

    =

    SSN	FName	LName	PNumber	PName	Hours
    111-11-1111	John	Smith	pj1	DBApplet	20
    111-11-1111	John	Smith	pj2	WebServer	10
    111-22-3333	Jane	Doe	pj1	DBApplet	5

  • The reconstructed content is the same as the original content !!!

    I.e., we have perserve the exact content - no more and no less

    ---

    ---

    ---

    ---

  • The Lemma 2 tells us that this decomposition will be a lossless decomposition:

    Employee1(SSN, FName, LName, PNumber, PName, Hours) into: R1 (SSN, FName, LName) R2 (SSN, PNumber, PName, Hours)

    This decomposition is lossless because:

    (1) R1 ∩ R2 = (SSN) and (2) SSN → SSN, FName, LName = R1 !!! Therefore: R1 ∩ R2 → R1 This property - according to Lemma 2 - guarantees that the decomposition is lossless !!!