The page table also contains information about the whereabout of the program store on disk.

The memory is divided into equal sizes called frames.

A common pages size is 1 to 4 Kbytes, because hard disks performs better when a larger chunch of data is transfered. (The access data on a hard disk, the hard disk has to move the disk head over the track that contains the data which is pretty slow).

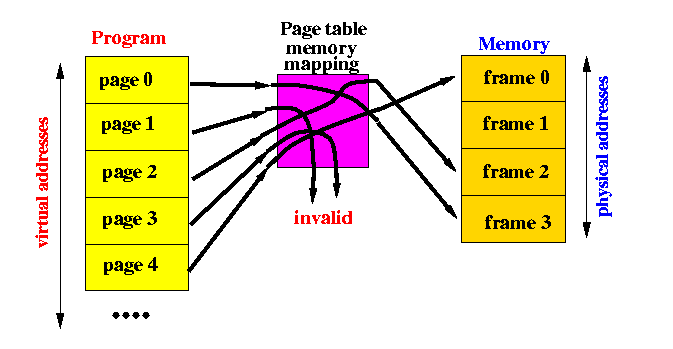
The page table defines a mapping between program pages and memory frames:

• Note that a page number is mapped to a memory frame number only when the page is present in memory.

  So pages 0, 1 and 4 are present in memory.

• If a page is not currently in memory, the memory mapping will return the invalid result.

  So pages 2 and 3 are not present in memory (the mapping results in invalid).

• Make sure that you realise that the mapping is from a page number to a frame number

• So to make paging work, we must find ways to
  • obtain the page number from the program address quickly and

  • then obtain the frame number from the page number quickly.

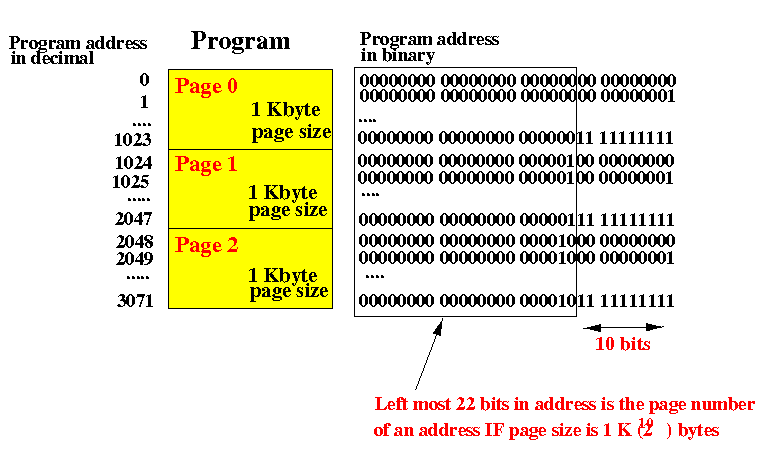
We make sure (by choosing the right page size) that the page size is always some power of 2 so that it is very easy to determine the page number for any given address.

For example, if the page size (and frame size) is 1 K bytes, the the left most 22 bits in a program address is equal to the page number:

Similarly, if the page size (and frame size) is 2 K bytes, the the left most 21 bits in a program address is equal to the page number, and so on.

This is the crux of the paging technique. Note that the mapping must be dynamic.

A simple and efficient dynamic mapping can be constructed by using a address translation table that map program page numbers to memory frame numbers.

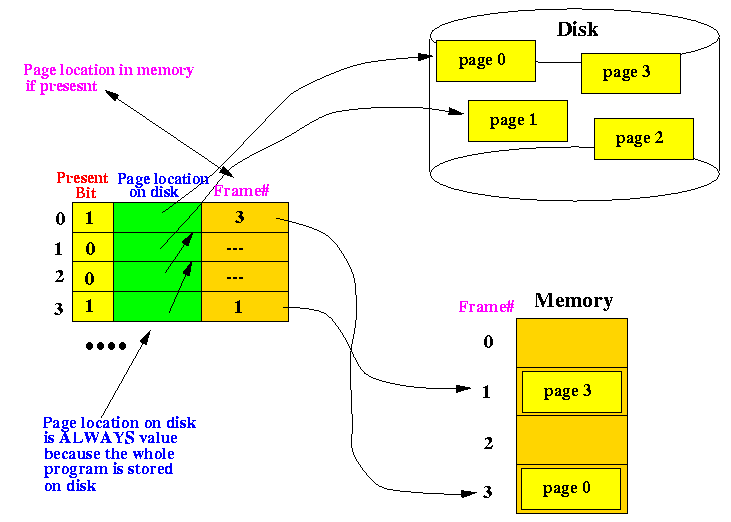
Because the total number of program pages is much larger than the number of frames in memory, no all pages of the program will be present in memory.

The mapping function has a special bit to indicate whether a page is present in memory and the address mapping is only valid when the page is present in memory.

• The location of the program page on disk is also stored in the page table.

  This location will be needed when the program tries to access a program location in a page that is not present in memory

• If the computer tries to access a program location in a page that is not present in memory, the translation table will be able to detect this (present bit = 0).

  The computer system can use the location on disk stored in the associated entry to read the page from disk and put it into the memory !program

We have 64 K memory (16 bit address for memory address !!!) Yet, we regularly write programs that can be as large as 4 G bytes (= 32 bit program address)

I will show you how this can be done now...

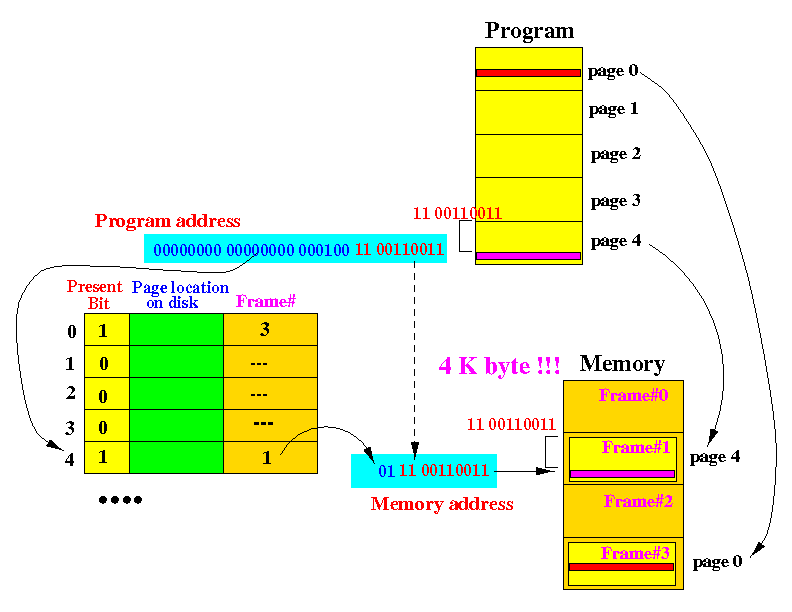
Page 0 of the program is currently stored in frame 3 in the memory Page 3 of the program is currently stored in frame 1 in the memory

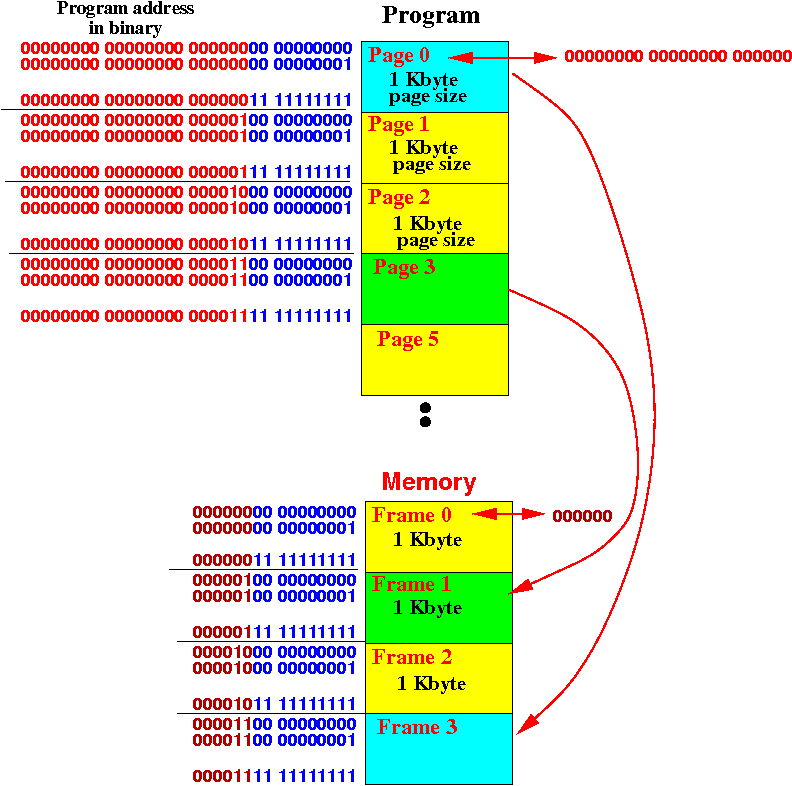
The following diagram shows the address mapping in detail:

Same sample of program address to memory address mapping values:

Program Address ---------> Memory address -------------------------------------------------------------- 00000000 00000000 00000000 00000000 00001100 00000000 00000000 00000000 00000011 11111111 00001111 11111111 00000000 00000000 00001100 00000000 00000100 00000000 00000000 00000000 00001111 11111111 00000111 11111111

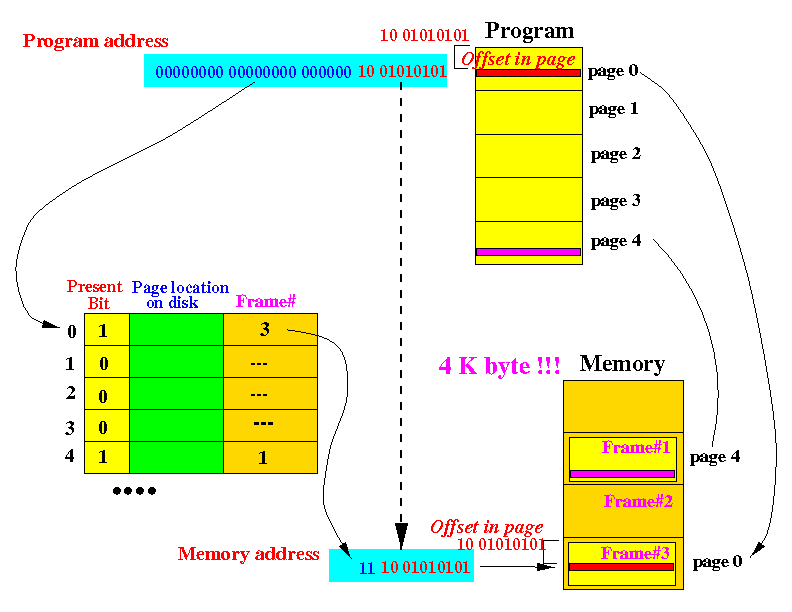
Here is a pictorial summary of the steps to translate a program address in page 4: into a memory address.

(Notice the memory can only hold 4 pages and the program address is in the 5^th page (page 4 is the 5^th page) !!!)

• When given a program address, the page number is first "computed" (removing bits is not much of a computation....)

• The page number is used as an index in the page table to look up the frame number.

• The frame number is concatenated with the offset of the program address to obtain the memory address

• The memory address is then used to access memory.

• Notice that in paging the number of bits in the program address and the memory address can be DIFFERENT !

  The reason is:

  • The length of the program address is defined by the manufacturer of the CPU (who defines the format of the machine instruction, specifically, how many bit did the manufacturer use to represent a program address).

  • The length of the memory address depends on how much memory you have installed in the computer. (You only need enough bits to identify each memory location that you have, ain't gonna do you any good to assign addresses to memory locations that you do not have...)

  Clearly they can be of different length....

  (In fact, if you add more memory, you will need more address wires to address the extra memory)

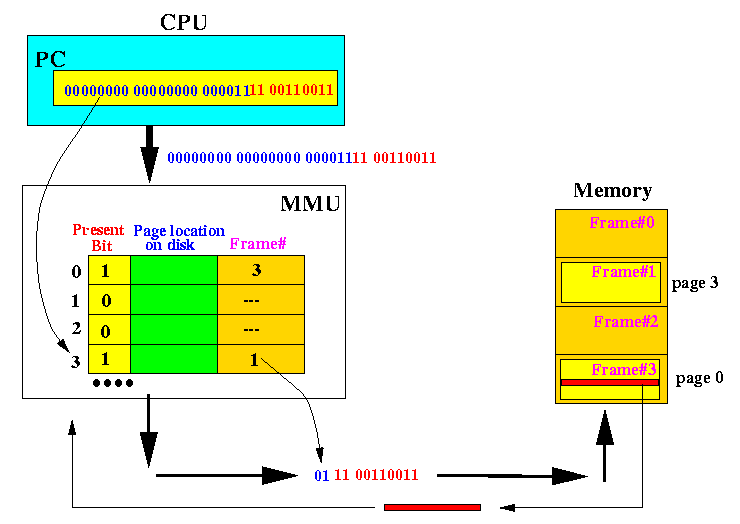
• First, you have to remember that the CPU is used to execute program instructions

• So the program counter contains a program address (and not a memory address).

• Also, assembler instructions can refer to variable stored in memory, but the address of the variable is a program address !

  E.g., the address indicated by "Label" in the assembler instruction "MOVE Label, D0", refers to an address in the program

• The above figure shows how the CPU fetches the next instruction:
  • The CPU sends out the value of the PC on the address bus.

  • This address is a program address and it is first translated by the MMU (using the page table) into a memory address

  • This memory address is then used to signal the memory to retrieve the instruction.