The "ripple borrow" subtractor for binary numbers

  • Similar to the ripple carry adder circuit, we can use the same technique to construct a ripple borrow subtractor circuit

  • The design of the ripple borrow subtractor circuit: 

                       BorrowIn = 1            
                 <--- 
         1      1      0
      +  1      0      1
    -------------------------

    In order to subtract a pair of corresponding bits, we only need to know whether the subtraction of the previous pair produced a borrow (=1)

But there is another way to perform subtraction with fixed length binary numbers !!!

Review: negating a 2s complement code
 

In CS255, we have learn this method to find the 2s complement representation for −x: 

                       x =  00000011   (repr: 3 decimal)

 (1)  flip all bits:        11111100
 (2)  add 1                 11111101   (repr: -3 decimal)

Because: a − x ≡ a + (−x), we can use the full adder circuit to construct a subtractor circuit !!!

Designing a 4 bits subtraction circuit
 

We start with the 4 bits addition circuit:

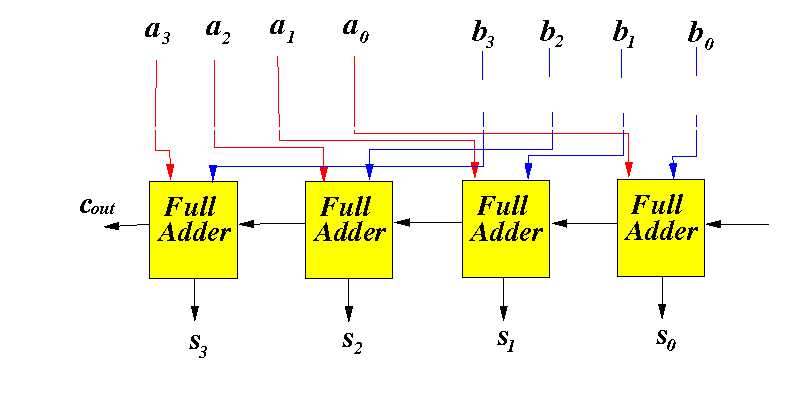
Note:   a − b ≡ a + (−b)

And:   − b ≡ (1) flip the bits in b and (2) add 1

Designing a 4 bits subtraction circuit
 

(1) Flip all bits in the binary number "b":

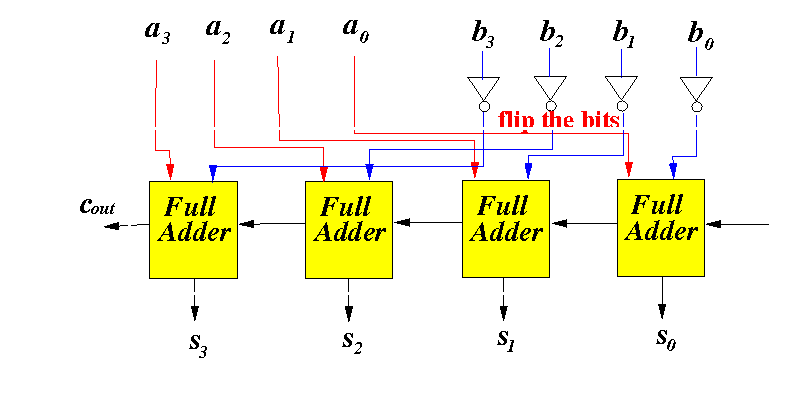
Note:   a − b ≡ a + (−b)

And:   − b ≡ (1) flip the bits in b and (2) add 1

Designing a 4 bits subtraction circuit
 

(2) Add 1 (we can use the carry input of the first full adder):

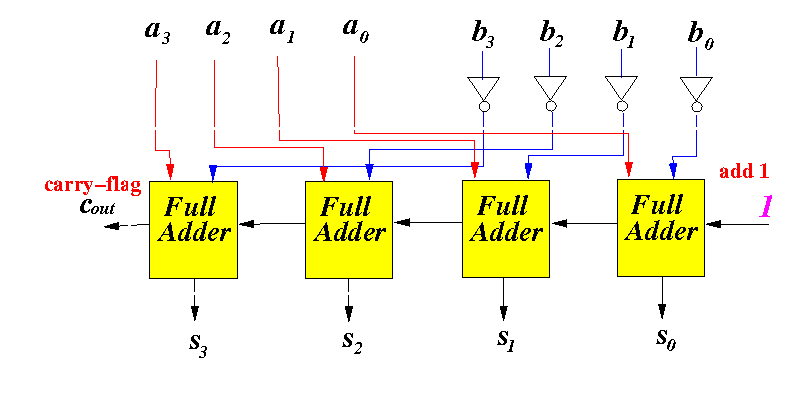
Note:   a − b ≡ a + (−b)

And:   − b ≡ (1) flip the bits in b and (2) add 1

Designing a 4 bits subtraction circuit
 

We must also adjust the carry output...

It turns out that negating cout will give us the correct signal for borrow (no explanation to save time)

DEMO: /home/cs355001/demo/circuits/4-bit-subtract