A circuit design problem

Problem description:

Design a digital circuit with:

3 inputs: a, b, c and
1 output: z

where:

The value of the output (z) is equal to 1 if two or more of the input values are equal to 1
Otherwise: the value of the output (z) is equal to 0

A circuit design algorithm

Step 1: list out every combination of the input values

a b c | z ---+---+---+--- 0 0 0 | 0 0 1 | 0 1 0 | 0 1 1 | 1 0 0 | 1 0 1 | 1 1 0 | 1 1 1 |

A circuit design algorithm

Step 2: determine the output for each combination of input values

a b c | z ---+---+---+--- 0 0 0 | 0 (< 2 input values = 1) 0 0 1 | 0 1 0 | 0 1 1 | 1 0 0 | 1 0 1 | 1 1 0 | 1 1 1 |

A circuit design algorithm

Step 2: determine the output for each combination of input values

a b c | z ---+---+---+--- 0 0 0 | 0 0 0 1 | 0 (< 2 input values = 1) 0 1 0 | 0 1 1 | 1 0 0 | 1 0 1 | 1 1 0 | 1 1 1 |

A circuit design algorithm

Step 2: determine the output for each combination of input values

a b c | z ---+---+---+--- 0 0 0 | 0 0 0 1 | 0 0 1 0 | 0 (< 2 input values = 1) 0 1 1 | 1 0 0 | 1 0 1 | 1 1 0 | 1 1 1 |

A circuit design algorithm

Step 2: determine the output for each combination of input values

a b c | z ---+---+---+--- 0 0 0 | 0 0 0 1 | 0 0 1 0 | 0 0 1 1 | 1 (≥ 2 input values = 1) 1 0 0 | (And so on)... 1 0 1 | 1 1 0 | 1 1 1 |

A circuit design algorithm

Complete table:

a b c | z ---+---+---+--- 0 0 0 | 0 0 0 1 | 0 0 1 0 | 0 0 1 1 | 1 1 0 0 | 0 1 0 1 | 1 1 1 0 | 1 1 1 1 | 1

A circuit design algorithm

End of Step 2: we have determined the output for each combination of input values

This table is called a logic table of the design function

Click on table to pull out

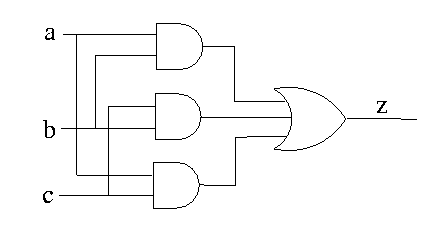
Use the logic table to construct the digital circuit

Step 1: draw the input signals and the output signal(s)

Use the logic table to construct the digital circuit

Step 2: add the NOT-gates to obtain all possible input combinations:

A combination of inputs is selected by connecting to the appropriate set of signals

Use the logic table to construct the digital circuit

Step 3: use one AND gate to compute each z=1 output in the logic table

x1 = 1 if and only if a = 0, b = 1, c = 1

Use the logic table to construct the digital circuit

Step 3: use one AND gate to compute each z=1 output in the logic table

x2 = 1 if and only if a = 1, b = 0, c = 1

Use the logic table to construct the digital circuit

Step 3: use one AND gate to compute each z=1 output in the logic table

x3 = 1 if and only if a = 1, b = 1, c = 0

Use the logic table to construct the digital circuit

Step 3: use one AND gate to compute each z=1 output in the logic table

x4 = 1 if and only if a = 1, b = 1, c = 1

Use the logic table to construct the digital circuit

Step 4: use one OR gate to combine all cases for z=1

z = 1 if and only if for input values that form cases x1, x2, x3 and x4

EDiSim circuit program for the digital circuit

Switch aa A '0' ZERO; Not aa A nA; Switch ba B '1' ZERO; Not ba B nB; Switch ca C '2' ZERO; Not ca C nC; And bb nA B C x1; And bb A nB C x2; And bb A B nC x3; And bb A B C x4; Or bd x1 x2 x3 x4 z; Probe be z;

DEMO

I will demo this circuit in class:

Circuit file: /home/cs355001/demo/circuits/majority

Post discussion: different circuits, same function

The same logic function can be implemented by different digital circuits !!
Previously, we saw this implementation of the majority function:
This circuit uses a smaller number of gates to implement the majority function !

The circuit optimization problem

Circuit optimization = finding the "best" digital circuit for a given logic function
The "best" circuit is a circuit that uses the least number of gates
The circuit optimization problem is NP-complete
(I.e.: we do not have a fast algorithm to solve the circuit optimization problem)

Note on CS355

In CS355, our goal is to show you how a computer works (at the gate level)
I will show you the internals of a (simple) computer using non-optimized digital circuits that perform the required logical functions
We will not perform any circuit optimization in CS355