- A method that invokes itself directly or indirectly
Example: direct recursive method
public class myClass
{
....
public (static) ... recursiveMethod(...)
{
...
...
recursiveMethod(new set of parameters)
...
...
}
}
|
Example: indirect recursive method
public class myClass
{
....
public (static) ... recursiveMethod1(...)
{
...
...
recursiveMethod2(.....)
...
...
}
public (static) ... recursiveMethod2(...)
{
...
...
recursiveMethod1(.....)
...
...
}
}
|
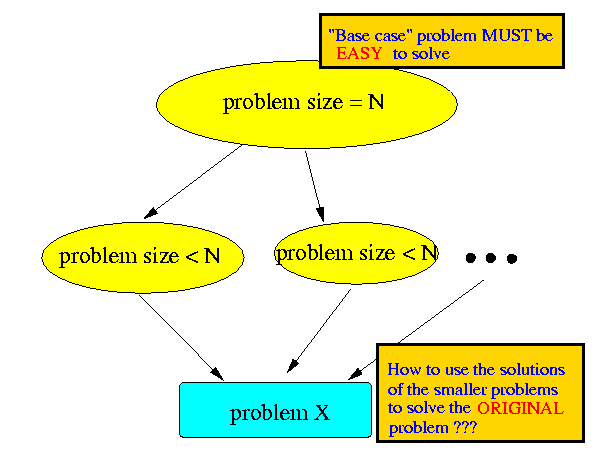
- The problem of size "N" can
be divided into:
- One or more
identical
problems of size less than N
- A solution
is known for one or more
base cases
of the problem
(the base cases are easy to solve)
- A problem X that is solved easily using the solutions for smaller problems
- One or more
identical
problems of size less than N
- If a problem has the above characteristic, the solution can be coded as follows:
General structure of a Recursive Solution
public ... recursiveSolve("problem N")
{
if ( "problem N" is a base case )
{
return( (known) solution for base case );
}
else
{
Split "problem N" into k smaller "problems < N"
and a "problem X"
sol_1 = recursiveSolve("smaller problem 1");
sol_2 = recursiveSolve("smaller problem 2");
....
sol_k = recursiveSolve("smaller problem k");
solution = solve "problem X" using the solutions
"sol_1", "sol_2", ..., "sol_k"
return(solution);
}
}
|
- Example: Compute the factorial of 12 (12!)
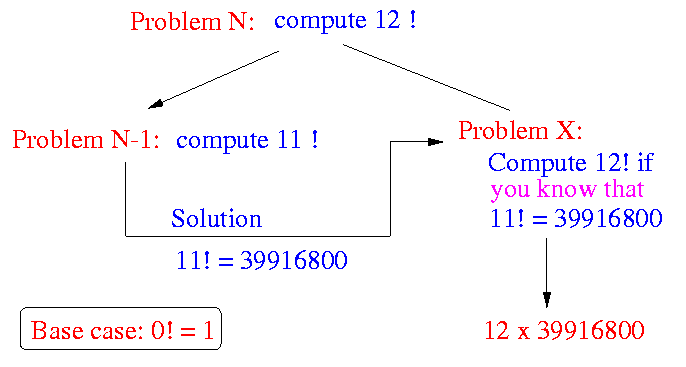
The recursive program:
Recursive Method to find Factorial of integer N
public class Numeric
{
public static int factorial(int N)
{
if ( N == 0 )
{
return( 1 ); // (known) solution for base case
}
else
{
int sol;
int solX;
sol = factorial(N-1);
solX = N * sol;
return(solX);
}
}
}
|
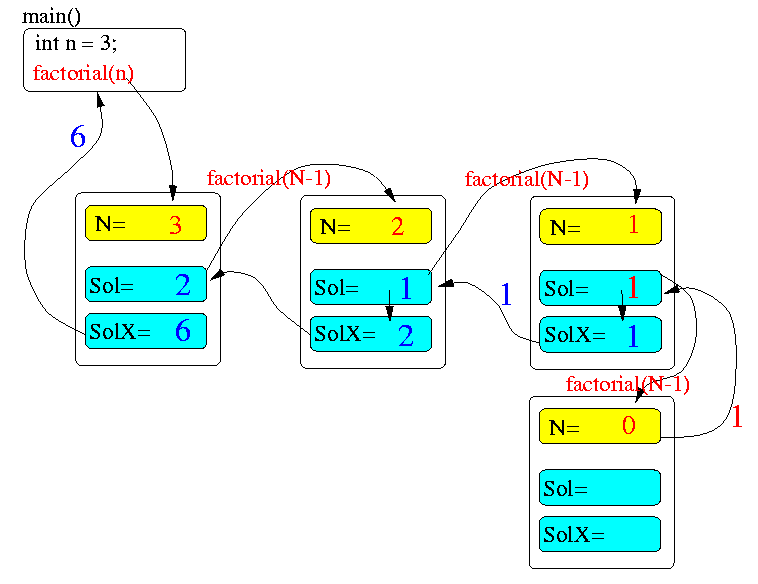
- When a method is invoked at
different times,
a different set
of parameters & local variables is created.
- Parameters & local variables
continue to exist
until their scope is exited
(that's why you need to understand scoping very well to understand recursion)
- Down to earth version: DEMO program: click here
- Nicer looking version: DEMO program: click here