An in-depth study of recursion

Review of the recursion concept:

  • Recursion = defining "something" in terms of itself

  • Example: 

        Non-recursive definition of factorial of n:

      n! = n*(n-1)*(n-2)*...*2*1          

  Recursive definition of factorial of n:

      n! = n*(n-1)! 
      0! = 1

  • A recursive definition must have at least one base case to terminate the recursive use of the definition

An in-depth study of recursion

Review of recursive functions:

  • Recursive function = a function that calls itself (in the body of the function)

  • Example: 

        int fac(int n)
  {
     if ( n == 0 )
        return 1;             // Base case
     else
        return n*fac(n-1);    // Recursion    
  }

  • Recursive functions must have at least one base case to terminate the recursive calls

When can we use recursion to solve a problem ?
 

Purpose of this lecture:

  • Students are often are taught the "what"/"how" of recursion

    Example:

      • How to write a recursive function (e.g.: find and write out the base cases, write the recursive call(s), etc)

  • Often, students do not learn the "when"/"why" of recuresion:

      • When can you use recursion ?
      • Why can you use recursion to solve a (complex) problem ?

When can we use recursion ?
 

Suppose we need to solve a problem of size n:

 

When can we use recursion ?
 

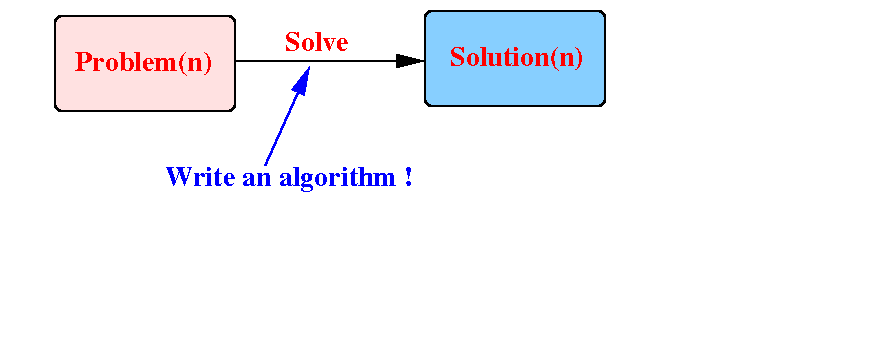
Consider the other identical (but) smaller problems:

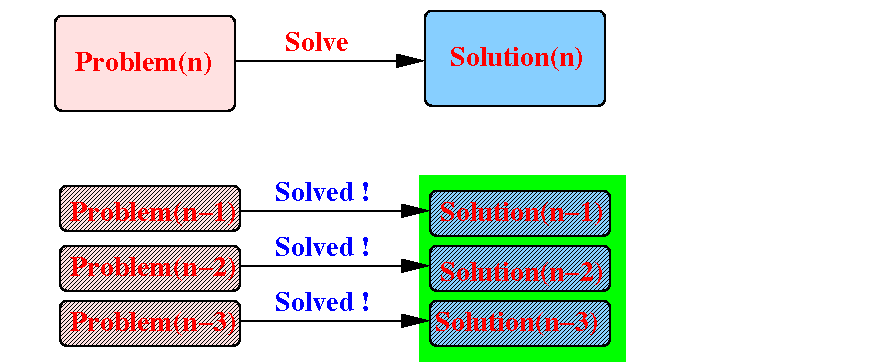
Suppose that we (already) have the solutions for all the smaller problems, i.e.: we do not need to solve them

Recursion = a divide and conquer algorithm
 

If we can construct Solution(n) using the solutions of the smaller problems:

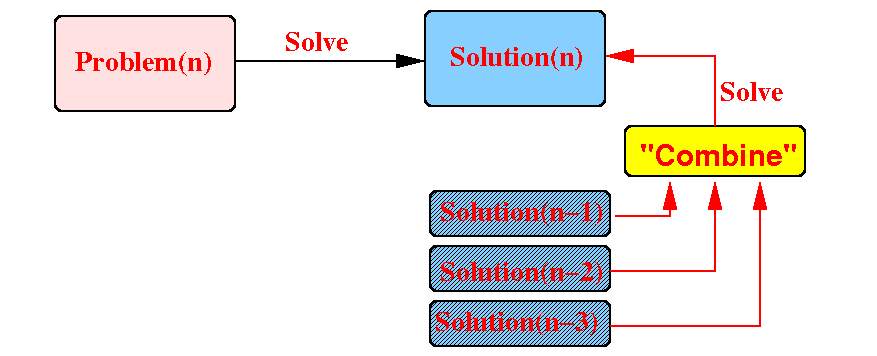
Then: we can use recursion to solve Problem(n) !!!

Example: why we can use recursion to compute the factorial function
 

Suppose we need to compute fac(10):

 

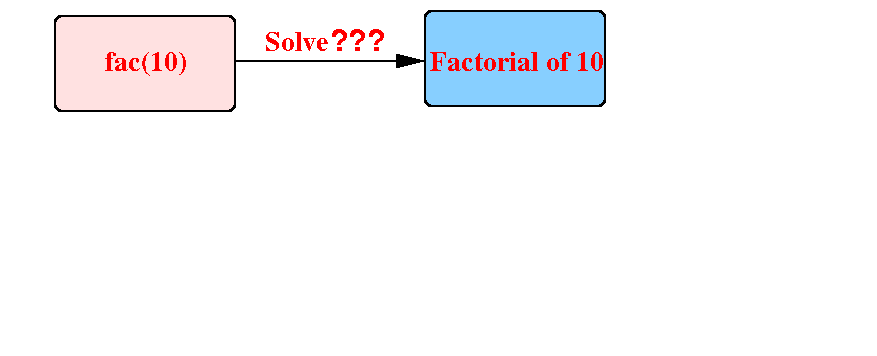
Recursion = a divide and conquer algorithm
 

Consider the smaller problem of fac(9):

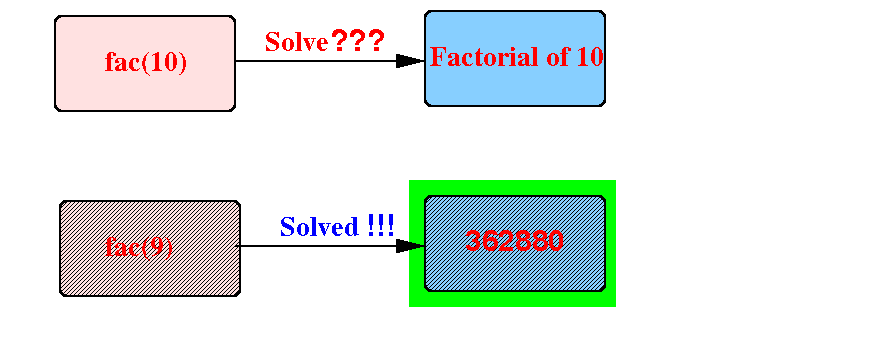
Question: can we solve fac(10) using the value 362880 ?

Recursion = a divide and conquer algorithm
 

We can compute fac(10) using the value 362880 as follows:

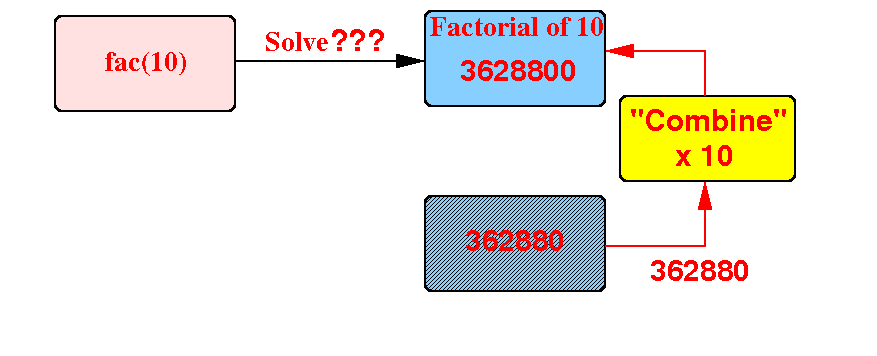
Therefore: we can write factorial as a recursive function !

How recursion actually works (hint: it's not calling yourself !)
 

Why you can use recursion to compute 10!:

Situation:   I have an idea how to do it....

How recursion actually works (hint: it's not calling yourself !)
 

Situation:   I know that 10! = 10 × 9!

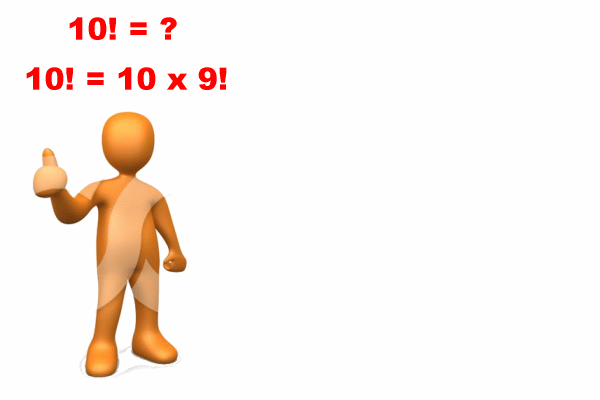
However:   I will need the solution for 9!...

How recursion actually works (hint: it's not calling yourself !)
 

I will delegate the 9! problem to a helper (someone else):

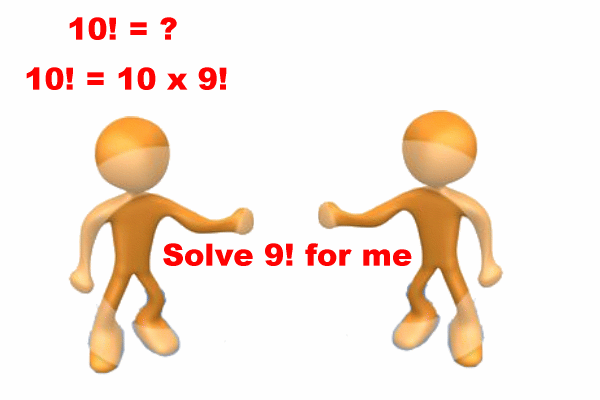
This technique is called divide and conquer and another process will solve the smaller problem

How recursion actually works (hint: it's not calling yourself !)
 

After I delegated the problem 9! to a helper (another person), I will wait for an answer

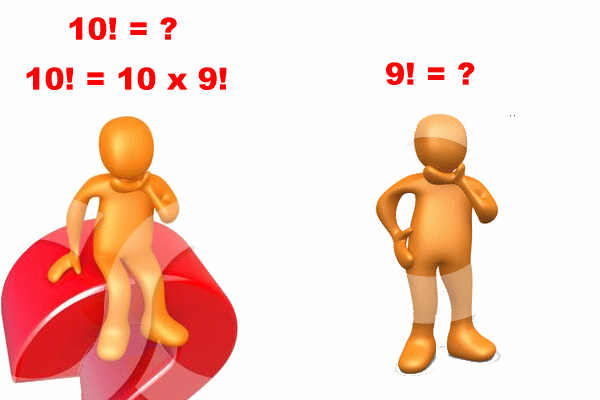
BTW: the helper that solves 9! is not the original person !!

How recursion actually works (hint: it's not calling yourself !)
 

Eventually (sooner or later), that helper (= another person) will be done:

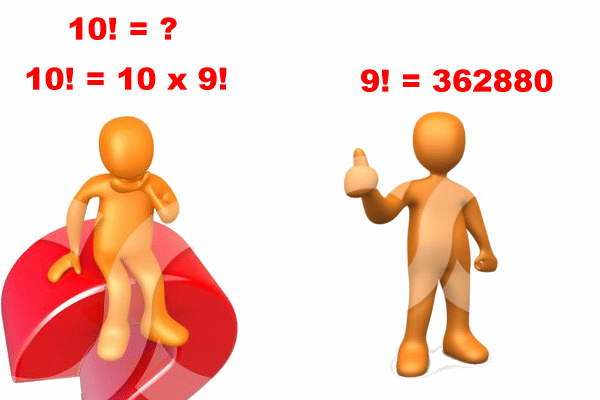
Meanwhile, I (= the original person) am still waiting for the answer...

How recursion actually works (hint: it's not calling yourself !)
 

The helper (= other person) give the answer 362880 to me (= original person):

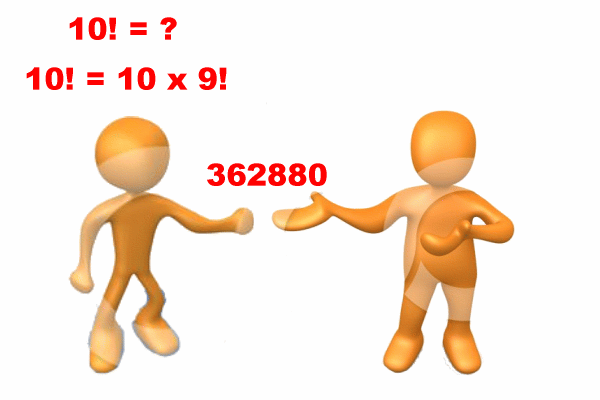
Notice:   I (= original person) only need the answer 362880. I don't need to know how he solved it !

How recursion actually works (hint: it's not calling yourself !)
 

I (= original person) can solve my problem 10!:

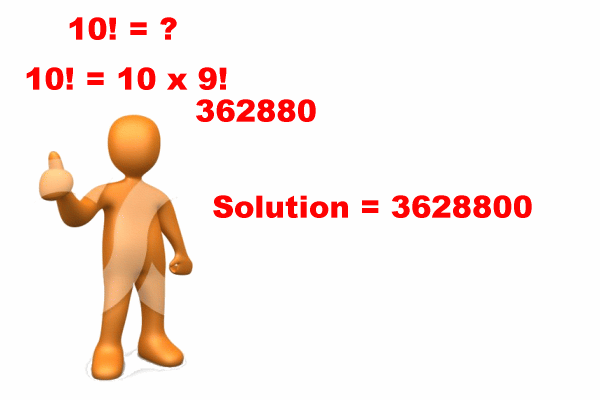
So: recursion is a divide and conquer problem solving technique !

The fac( ) function revisited
 

Students are usually taught the following fac( ) function: 

   int fac(int n)
   {
      if ( n == 0 )
         return 1;
      else
         return (n * fac(n-1));
   }

This form does not reveal how the divide-and-conquer technique was used...

The fac( ) function revisited

I teach students the following function in my intro CS class (Java): 

   int fac(int n)
   {
      int helpSol;     // Solution to the smaller problem
      int mySol;       // Solution to my problem

      if ( n == 0 )
         return 1;
      else
      {
         helpSol = fac(n-1); // Delegate a smaller problem to someone
                             // (helpSol will receive the solution) 
	 mySol = n*helpSol;  // Solve my problem using the 
                             // solution of the smaller problem 
         return (mySol);
      }
   }

This form reveals how the divide-and-conquer technique was used !

Important insight to help you understand and write recursive functions

You must distinguish between fac( ) that solves your problem and fac( ) that solves a smaller problem: 

   int fac(int n)  <--- This fac( ) represents "YOU" (solves your problem)
   {
      int helpSol;
      int mySol;

      if ( n == 0 )
         return 1;
      else
      {
         helpSol = fac(n-1);   <--- This fac( ) your "helper" ! 
                               This fac( ) solves a smaller problem
	 mySol = n*helpSol; 

         return (mySol);
      }
   }

So recursion will run another (copy of the) function