Hansel and Gretel and non-leaf functions
In the story of Hansel and Gretel, they lost the bread crumbs that point the way back home:
This analogy is also applicable in function calls because:
|
How can you
lose a
return address -
Example
Let's write this sequence of function calls using what we just learned:
public static void main(String[] args)
{
A( );
}
public static void A( )
{
...
B( ); // Calls B( )
...
}
public static void B( )
{
... // Does not call any method/function
...
}
|
How can you
lose a
return address -
Example
The function call code:
main:
mov r0, #1111
mov r1, #1111
bl A
mov r2, #2222
mov r3, #2222
Stop:
nop
A:
mov r0, #3333
mov r1, #3333
bl B // Overwrites lr (A's return address to main !)
mov r2, #4444
mov r3, #4444
mov pc, lr // A fails to return to main !!!
B:
mov r0, #9999
mov r1, #9999
mov pc, lr // B succeeds to return to A
|
DEMO: /home/cs255001/demo/asm/8-sub/bl+rts2.s
How can you
lose a
return address -
Example
Why the function A( ) cannot return to main( ):
main:
mov r0, #1111
mov r1, #1111
bl A // Saves return address to main in lr
mov r2, #2222 // <--- return address used by A
mov r3, #2222
Stop:
nop
A:
mov r0, #3333
mov r1, #3333
bl B // A has lost its return address to main !
mov r2, #4444
mov r3, #4444
mov pc, lr // Therefore: A cannot return to main !!!
B:
mov r0, #9999
mov r1, #9999
mov pc, lr
|
DEMO: /home/cs255001/demo/asm/8-sub/bl+rts2.s
How to implement
a non-leaf function
in ARM assembler
|
Question: which data structure should we use to save the return addresses ???
The order in which
return addresses are
used
Suppose:
main( ) -----> A( ) -----> B( )
{ { {
A( ); B( ); ...
} } }
|
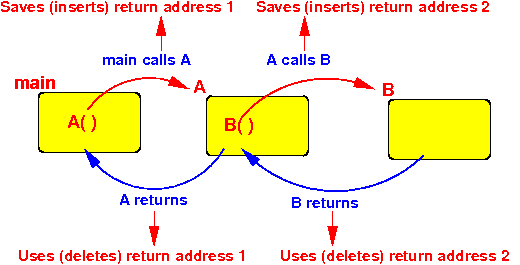
Return order is: Last In First Out (LIFO)
main( ) <----- A( ) <----- B( )
{ { {
A( ); B( ); ...
} } }
|
The data structure used
to store
return addresses
|