Interpreting 2s complement codes
Humans are trained to represent signed values using the sign-magnitude rperesentation:
Interpreting 2s complement codes
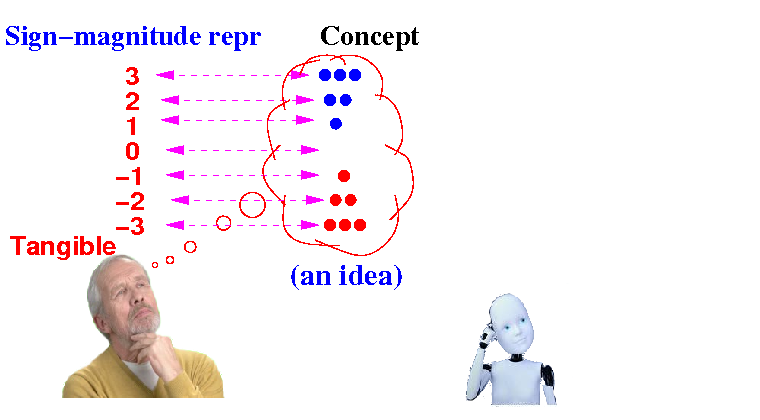
Computers are programmed to represent signed values using the 2s complement codes:
Interpreting 2s complement codes
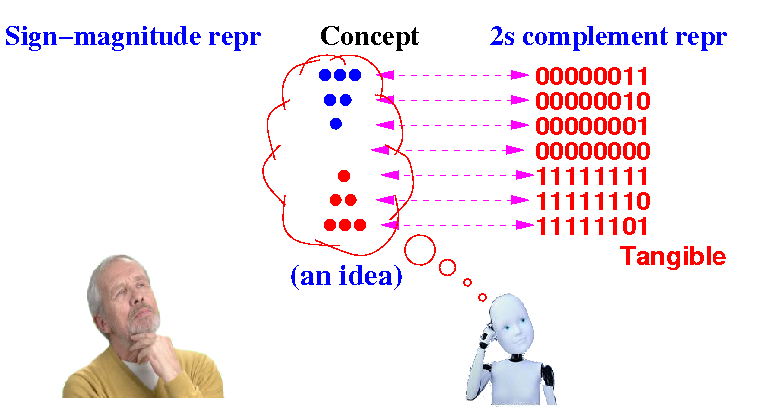
Question: how do we convert between these 2 representations ?
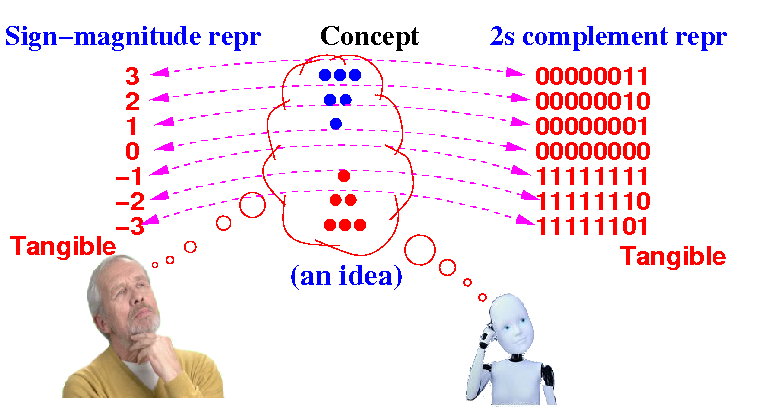
Note: the conversion must preserve the represented value !!
Converting a decimal sign-magnitude code
into a
(8 bits) 2s complement code
Question: what are the (8 bits) 2s complement code for 34 and −34 ?
Consider the mapping that we discussed previously:
2s comp Intrinsic Decimal Code value sign-magnitude repr ================================================================ 10000000 -128 ..... .... .... ???????? <--------------------------------- -34 ..... .... .... 11111011 ••••• -5 11111100 •••• -4 11111101 ••• -3 11111110 •• -2 11111111 • -1 00000000 ( ) 0 00000001 • 1 00000010 •• 2 00000011 ••• 3 00000100 •••• 4 00000101 ••••• 5 ..... .... .... ???????? <--------------------------------- 34 ..... .... .... 01111111 127 |
The relationship will be clearer using the binary sign-magnitude representation
Converting a decimal sign-magnitude code
into a
(8 bits) 2s complement code
Question: what are the (8 bits) 2s complement code for 34 and −34 ?
Consider the mapping (relationshp) between the 2s complement code and the binary sign-magnitude code:
2s comp Intrinsic Binary Decimal Code value sign-mag repr sign-magnitude repr ================================================================ 10000000 -128 ..... .... .... ???????? <--------------------------------- -34 ..... .... .... 11111011 ••••• -101 -5 11111100 •••• -100 -4 11111101 ••• -11 -3 11111110 •• -10 -2 11111111 • -1 -1 00000000 ( ) 0 0 00000001 • 1 1 00000010 •• 10 2 00000011 ••• 11 3 00000100 •••• 100 4 00000101 ••••• 101 5 ..... .... .... ???????? <--------------------------------- 34 ..... .... .... 01111111 127 |
(1) Positive
(binary) numbers:
differs in using
leading
0 digits
(2) Negative:
2s compl code +
abs(bin sign-magnitude) = 100000000
Converting a decimal sign-magnitude code
into a
(8 bits) 2s complement code
Converting from decimal sign-magnitude ⇒ binary 2s complement is a 2 step process:
2s comp Intrinsic Binary Decimal
Code value sign-mag repr sign-magnitude repr
================================================================
10000000 -128
..... .... ....
???????? <--------------------------------- -34
<------- step 2 ------------ <--- step 1 ---
11111011 ••••• -101 -5
11111100 •••• -100 -4
11111101 ••• -11 -3
11111110 •• -10 -2
11111111 • -1 -1
00000000 ( ) 0 0
00000001 • 1 1
00000010 •• 10 2
00000011 ••• 11 3
00000100 •••• 100 4
00000101 ••••• 101 5
<------- step 2 ------------ <--- step 1 ---
???????? <--------------------------------- 34
..... .... ....
01111111 127
|
Converting
decimal sign-mag code to
2s compl code is
a
2 step process:
(1)
convert
decimal
sign-mag representation
→
binary
sign-mag repr
(2) convert
binary
sign-mag representation
→
2s compl code
Note:
You must
handle
positive/negative values
differently !
Converting a decimal sign-magnitude code
into a
(8 bits) 2s complement code
How to convert a positive sign-magnitude code into a (8 bits) 2s complement code:
2s comp Intrinsic Binary Decimal
Code value sign-mag repr sign-magnitude repr
================================================================
10000000 -128
..... .... ....
???????? <--------------------------------- -34
<------- step 2 ------------ <--- step 1 ---
11111011 ••••• -101 -5
11111100 •••• -100 -4
11111101 ••• -11 -3
11111110 •• -10 -2
11111111 • -1 -1
00000000 ( ) 0 0
00000001 • 1 1
00000010 •• 10 2
00000011 ••• 11 3
00000100 •••• 100 4
00000101 ••••• 101 5 <--- Example
<------- step 2 ------------ <--- step 1 ---
???????? <--------------------------------- 34
..... .... ....
01111111 127
|
Converting
positive values (and ZERO):
(1)
Convert the
decimal
sign-magnitude code into
the (unsigned)
binary represention
(2)
Prepend the resulting
binary sign-magnitude code with
leading ZEROs
Example: Converting 34 into a
(8 bits) 2s complement code
(1) Example: convert the decimal sign-magnitude code (34) into binary (by dividing by 2)
34
2 --------- 0 34(10) = 100010(2)
17
2 --------- 1 (binary sign-magnitude repr)
8
2 --------- 0
4
2 --------- 0
2
2 --------- 0
1
2 --------- 1
0
|
(2) Prepend the resulting binary sign-magnitude code with leading ZEROs until you have 8 bits
binary sign-mag repr 8 bits 2s compl repr (fixed length)
---------------------- ----------------------
100010 00100010
|
Note: to convert to a 16 bits 2s complement repr, we must prepend more leading 0's (8 more) !!
Converting a decimal sign-magnitude code
into a
(8 bits) 2s complement code
How to encode a negative decimal sign-magnitude code into a (8 bits) 2s complement code:
2s comp Intrinsic Binary Decimal Code value sign-mag repr sign-magnitude repr ================================================================ 10000000 -128 10000001 -127 ..... .... .... ???????? <--------------------------------- -34 <------- step 2 ------------ <--- step 1 --- 11111011 ••••• -101 -5 <--- Example 11111100 •••• -100 -4 11111101 ••• -11 -3 11111110 •• -10 -2 11111111 • -1 -1 00000000 ( ) 0 0 00000001 • 1 1 00000010 •• 10 2 00000011 ••• 11 3 00000100 •••• 100 4 00000101 ••••• 101 5 <------- step 2 ------------ <--- step 1 --- ???????? <--------------------------------- 34 ..... .... .... 01111111 127 |
Converting
negative values (and ZERO):
(1)
Convert the
positive decimal sign-magnitude code into a
binary number (dividing by 2
repeatedly)
(2)
Subtract the
binary number in
step (1) from the
binary number
100000000
(=
negation)
(The
negation
operation on
2s complement codes
will be explained later
after
1 more slide)
Example: converting −34 into a
(8 bits) 2s complement code
(1) Convert the positive decimal sign-magnitude code (34) into binary
34
2 --------- 0 34(10) = 100010(2)
17
2 --------- 1 (binary sign-magnitude repr)
8
2 --------- 0
4
2 --------- 0
2
2 --------- 0
1
2 --------- 1
0
|
(2)
Negate:
subtract the resulting
binary number (100010 from
100000000
100000000 (Because: 00100010 + ??? = 100000000)
- 100010
-------------
11011110 <--- 2s compl code for -34(10)
|
Note:
100000000
(1 with 8 (eight)
ZEROS) is
only used for the
8 bit
2s complement code
Different bit length must use
a different constant
How to
negate
a 2s complement representation
Problem statement:
|
Because x + y = 0, we have for a 8 bits 2s complement code:
2s comp Decimal Code Sign-Magnitude ======================== 10000000 -128 10000001 -127 ..... 11111100 -4 11111101 -3 11111110 -2 11111111 -1 x + y = 00000000 00000000 0 y = 00000000 - x 00000001 1 00000010 2 We will actually compute: 00000011 3 y = 100000000 - x 00000100 4 because we need to borrow to subtract ..... 01111111 127 |
How to negate a 2s complement representation
2s comp Decimal Code Sign-Magnitude ======================== ..... 11111100 -4 (2s compl code for x) + (2s compl code for -x) = 0000.....00 11111101 -3 11111110 -2 11111111 -1 00000000 0 00000001 1 00000010 2 00000011 3 00000100 4 ..... |
Given:
01001001
is the 8 bits
2s complement code for
73
Question:
what is the
8 bits
2s complement code for
−73 ?
Let y = 8 bits 2s complement code for -73, then:
y + 01001001 = 00000000 (do the operation with 8 bits only)
<==> y = 00000000 - 01001001
00000000 (Do subtraction in 8 bits 2s compl code)
- 01001001
------------
10110111
|
Easier way
to negate a 2s complement representation
Previously:
8-bits 2s compl code for −x = 100000000 − 2s compl code for x |
Easier way to compute the difference 100000000 − anyBinNumber:
100000000 − x Example flip-bits(x)
<==> (11111111+1) − x 11111111
<==> (11111111 − x ) + 1 - 01011010
<===> flip-bits(x) + 1 -----------
10100101
|
Example:
Original method Easier method
100000000 flip-bits
- 00000011 00000011 ---> 11111100
----------- 1
11111101 ---------
11111101
|
Converting
2s compl code →
decimal sign magnitude representation
Problem statement:
|
Converting
2s compl code →
decimal sign magnitude representation
Problem statement:
|
To find the solution, examine the mapping:
2s comp Decimal Code Sign-Magnitude ======================== 10000000 -128 10000001 -127 ..... 11111100 -4 // Negative values are harder to see 11111101 -3 11111110 -2 11111111 -1 00000000 0 00000001 1 00000010 2 00000011 3 00000100 4 // Positive values are "easy" to see ..... // Same as the bin number system !! 01111111 127 |
We must split into 2 cases: (1) positive 2s compl codes and (2) negative 2s compl codes
How to tell
if a 2s complement code represents
a
positive/negative value ?
Look at the left-most digit in the 2s complement code:
2s comp Decimal Code Sign-Magnitude ======================== 10000000 -128 10000001 -127 ..... 11111100 -4 // Negative values 11111101 -3 11111110 -2 11111111 -1 00000000 0 00000001 1 00000010 2 00000011 3 00000100 4 // Positive values ..... 01111111 127 |
Left-most bit = 1 in
2s complement code
⇒ represents a negatve value
Left-most bit = 0 in
2s complement code
⇒ represents a positive value
(or ZERO)
Converting
2s compl code of a
positive value →
decimal sign magnitude representation
Algorithm: just use the method to convert binary numbers → decimal number
Example:
|
Converting
2s compl code of a
negative value →
decimal sign magnitude representation
Algorithm:
(1) negate the
2s complement code
(2) convert the
positive 2s compl code
using the
previous method
(3) add a
negative sign
to the asnwer
Example:
|