The Hexadecimal Number System
 

The Hexadecimal Number System:

  • Has 16 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

  • The value of a digit at the kth position is weighted by 16k  

 

I.e.: the hexadecimal number system is similar to the decimal/binary/octal number systems

Note: the symbols A, B, C, D, E, F are not used as letters !!!

The symbols A, B, C, D, E, F are digits with value equal to 10, 11, 12, 13, 14, 15, respectively !!!

Converting a hexadecimal number ⇒ decimal number
 

Example:

  • Find the decimal value represented by the Hexadecimal number BAD(16) ?  

Answer: (perform this computation in decimal arithmetic) 


    BAD(16) 
    ^^^
    |||
    ||+----- 13 * 160 = 13 *   1 =    13
    |+------ 10 * 161 = 10 *  16 =   160
    +------- 11 * 162 = 11 * 256 =  2816  +
                              ----------     
                                    2989(10)

Converting a decimal number ⇒ hexadecimal number
 

Example:

  • Find the hexadeciaml number representation for the decimal number 30(10)  

Answer: (perform this computation in decimal arithmetic) 

        30
   16 ------ 14  (= E)
         1
   16 ------ 1
         0

    The nexadecimal number for 30(10) is ----> 1E(16)

Displaying/printing binary numbers using hexadecimal numbers
 

Hex dump = a hexadecimal view (on screen or paper) of computer data
(Recall: data in computer is always in binary !!)

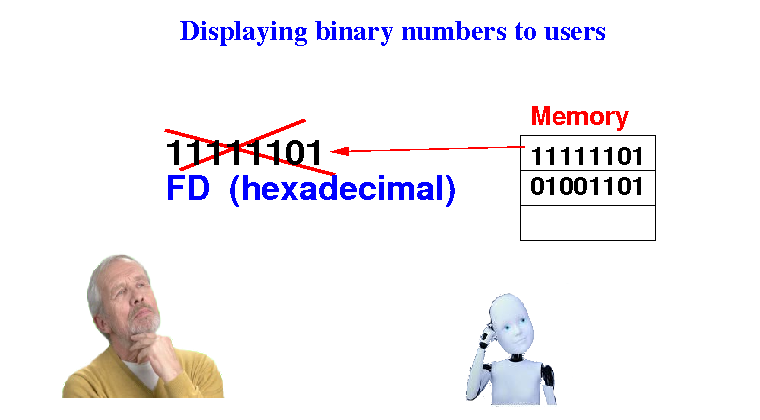
Hexadecimal representation is very well suited to display byte, short and int (binary) data

How to convert between binary representation <--> hexadecimal representation
 

Converting between binary representation <--> hexadecimal representation:

  • How to convert a binary number (= representation) → an hexadecimal number (= representation):

      • Convert a group of 4 binary digits individually into 1 hexadecimal digit

  • How to convert an hexadecimal number (= representation) → a binary number (= representation):

      • Convert each octal digit in the hexadecimal number individually into exactly 4 binary digits

 

Because the byte, short and int binary data consists of an integral multiple of 4 bits, the hexadecimal representation is perfectly suited for displaying byte, short and int binary data

Examples on how to convert:   binary numbers ⇒ hexadecimal numbers
 

Conversion table between 1 hexadecimal digit and 4 binary digits: 

 Hex digit      Binary digits    Hex digit      Binary digits  
 ---------      -------------    ---------      -------------   
    0      <-->     0000            8      <-->     1000
    1      <-->     0001            9      <-->     1001
    2      <-->     0010            A      <-->     1010
    3      <-->     0011            B      <-->     1011
    4      <-->     0100	    C      <-->     1100
    5      <-->     0101	    D      <-->     1101
    6      <-->     0110	    E      <-->     1110
    7      <-->     0111	    F      <-->     1111

   (Leading 0's can optionally be truncated)

Example 1:   11111011(2) ===> FB(16)

Example 2:   0111100111101010(2) ===> 79EA(16)

Example on how to convert:   hexadecimal numbers ⇒ binary numbers
 

Conversion table between 1 hexadecimal digit and 4 binary digits: 

 Hex digit      Binary digits    Hex digit      Binary digits  
 ---------      -------------    ---------      -------------   
    0      <-->     0000            8      <-->     1000
    1      <-->     0001            9      <-->     1001
    2      <-->     0010            A      <-->     1010
    3      <-->     0011            B      <-->     1011
    4      <-->     0100	    C      <-->     1100
    5      <-->     0101	    D      <-->     1101
    6      <-->     0110	    E      <-->     1110
    7      <-->     0111	    F      <-->     1111

   (Leading 0's can optionally be truncated)

Example:   4DB3(16) ===> 0100110110110011(2) (in 16 bits)

The hex dump

From Wikipedia:

The UNIX od command can output hex dumps. I will show this in class using these commands:

  
   cd /home/cs255001/demo/dump    

   od -t x1 bin-file  // -t x1 means: display 1 byte data in hex

         // Adding z will print corresponding letter if possible

Each hexadecimal number in the output represents 1 byte (or 8 bits)

Denoting octal numbers in Java

How to denote an octal number in Java:

  • When the leading digits = 0x, Java will treat the number as a hexadecimal number

Example: 

    int x = 10;    // Default is decimal
    int y = 0x10;  // Hex number !

    System.out.println(x);  // prints 10
    System.out.println(y);  // prints 16

DEMO: /home/cs255001/demo/java/Hexadecimal.java

Application:   you can write a binary number very compactly using hexadecimal numbers