Pre-requisite
to performing addition
in the base 10 positional number system
Pre-requisite to perform decimal addition
145
+ 61
--------
(You have done this in 3rd grade in elementary school) |
(Partial) Addition table for the decimal number system:
+ | 1 2 3 4 5 6 7 8 9 ---+---+---+---+---+---+---+---+---+---- 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 ---+---+---+---+---+---+---+---+---+---- 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |10 | 11 ---+---+---+---+---+---+---+---+---+---- .... etc etc |
Using the
(decimal) addition table
in an addition operation
Humans will become a "human calculator" after they have learned the (decimal) addition table:
Addition table of the binary number system
The binary number system also has an addition table:
0 1 0 1
+ 0 + 0 + 1 + 1
--- --- --- ---
0 1 1 10
^
|
+--- carry
|
Adding binary numbers works exactly like adding decimal numbers
The only difference is:
The carry happens when the total (= sum) ≥ 2
Will a binary addition
(always) give us the correct sum ?
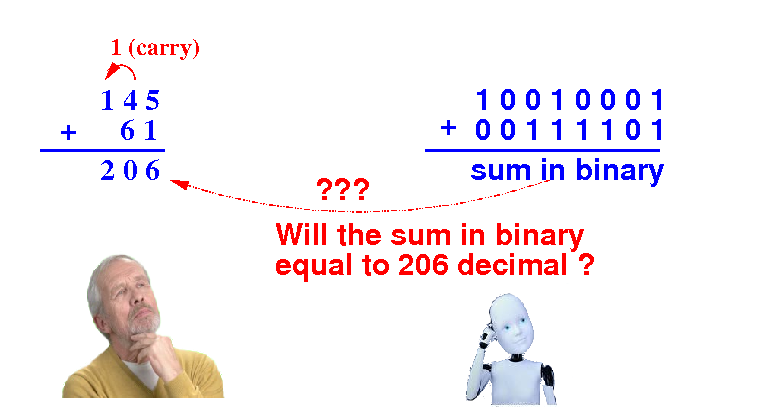
Suppose the
computer is
given the
binary representations for
the decimal numbers
145 and
61
Will a binary addition
(always) give us the correct sum ?
The computer performs the addition in binary using circuitry that implements the the binary addition table:
Comment: If you want to know about the computer circuits used to perform calculations, take CS355
Will a binary addition
(always) give us the correct sum ?
$64,000 question: will the sum in binary represent that correct sum value (206) ???
No proofs... I will give some examples to show you that this is a fact
Binary addition: A simple example
Example:
In decimal In binary
*** * = carry
5 ---> 00000101
+ 7 ---> + 00000111
---- ----------
12 <--- 00001100
|
I will do the addition step-by-step
in class:
00000101
+ 00000111
------------
Binary addition: A more complex example
Example:
In decimal In binary
** * * = carry
145 --> 10010001
+ 61 --> + 00111101
------- ----------
206 <-- 11001110
|
I will do the addition step-by-step
in class:
10010001
+ 00111101
------------
Subtraction table of the binary number system
Subtraction table for the binary number system:
0 1 0 1
- 0 - 0 - 1 - 1
--- --- --- ---
0 1 *1 0
^
|
+--- BORROW !
|
Subtracting binary numbers works exactly like subtracting decimal numbers
The only difference is:
When you borrow from you neighbor digit, you will receive 2 units
Binary subtraction: A simple example
Example:
In decimal In binary
* * = borrow
9 00001001
- 5 - 00000101
---- ----------
4 00000100
|
I will do the subtraction
step-by-step
in class:
00001001
- 00000101
------------
Binary subtraction: A more complex example
Example:
In decimal In binary
** * * = borrow
149 10010101
- 41 - 00101001
----- ----------
108 01101100
|
I will do the subtraction
step-by-step
in class:
10010101
- 00101001
------------
Multiplication table of the binary number system
Multiplication table for the binary number system:
0 1 0 1
x 0 x 0 x 1 x 1
--- --- --- ---
0 0 0 1
|
Multiplying binary numbers works exactly like multiplying decimal numbers
The only difference is:
Each time the sum reaches 2, you must generate a carry
Binary Multiplication: example
Example:
93(10) = 1011101(2)
13(10) = 1101(2)
1011101
x 1101
----------
1011101
101110100
1011101000
--------------
10010111001 (= 1209(10))
|
(I will do the multiplication
step-by-step in class):
Dicimal division vs binary division
Decimal division is hard !!!
Example:
0082 (quotient = 82(10))
---------
27 / 2237
0
---
22
0
---
223
216
----
77
54
---
23 (remainder = 23(10))
|
Binary division
Binary division is extremely easy:
|
Binary division - example
Example of a
binary division:
27(10) = 11011(2)
2237(10) = 100010111101(2)
000001010010 (quotient = 82(10))
-------------------
11011/ 100010111101
0
---
10
00
---
100
000
----
1000
0000
-----
10001
00000
------
100010
11011
-------
1111
0000
-------
11111
11011
-------
1001
0000
------
10011
00000
------
100110
11011
-------
10111
00000
------
10111 (remainder = 23(10))
|