Converting between decimal number representation and binary number representation
 

Problem Description: we have 2 different representations for (unsigned) numerical values:

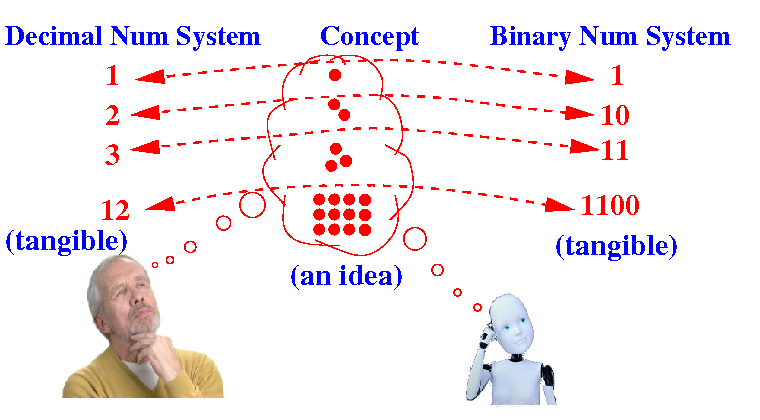
How do we convert between these 2 different representations ???

Why you must learn conversion between decimal and binary numbers

  • Humans are accostumed to use the decimal number system to represent integer (= whole) values

  • In contrast:   computer must use the binary number system...

    • Computer Science professionals must know the tool of their trade (= computer)

  • Therefore:

    • Converting between binary ⇆ decimal numbers a fundamental skill in Computer Science

    Examples: 

     Given: 10101 in binary  --> the decimal number 
                             for the same value = ??? 

 Given: 25    in decimal --> the binary number
                             for the same value = ???

How to convert from binary representation ⇒ decimal representation

  • To convert the binary representation to the decimal representation (for the same value), do the following:

      • Compute the decimal sum of the value of each (binary) digit multiplied by its "position factor"

  • Example: Convert the binary number 01011001 to a decimal number

    Worked out example: 

       Digits:           0   1   0   1   1   0   0   1
 Multiply factor:  27  26  25  24  23   22  21  20
                  128  64  32  16  8   4   2   1   
                   --------------------------------
                       64 +    16 +8         + 1 = 89 

 Answer:  01011001 binary  =  89 decimal

How to convert from decimal representation ⇒ binary representation

  • To convert the decimal representation to the binary representation (for the same value), do the following:

      • Divide the decimal representation repeatedly by 2     and  
      • Collect the remainders of the divisions in reverse order.

    Example: Convert the decimal number 13 to a binary number 

               13
    ÷2 ------- 1 (= remainder of  13 ÷ 2)         
          6
    ÷2 ------- 0 (= remainder of   6 ÷ 2)
          3
    ÷2 ------- 1 (= remainder of   3 ÷ 2)
          1
    ÷2 ------- 1 (= remainder of   1 ÷ 2)
          0

 Answer:  13 decimal = 1101 binary

Why programming languages have different integer data types

  • Java (and C) has different integer (= whole number) data types:

    • byte:   can represent/store values between −127 .. 128 (uses 1 byte)
    • short: can represent/store values between −32767 .. 32768 (uses 2 bytes)
    • int: can represent/store values between −2147483647 .. 2147483648
    • long: can represent/store values between −9223372036854775807 .. 9223372036854775808

  • The reason why programming languages provide different integer data types:

    • Computer memory was a scarce resource (used to be very expensive !)

    • Integer of different sizes allow the programmer to decide on a trade-off:

      • Shorter representations to minimize memory usage

      • Longer representations to maximize accuracy

    I.e.: you cannot (1) have the cake and (2) eat it...
    (My college professor calls this: The law of conservation of misery)

Storing integer (= whole) values inside a computer program
 

Important note:   the computer will only use these fixed lengths to store integer (= whole) numbers:

 
  • byte: uses 1 byte of memory (i.e.: 8 bits binary number)

  • short: uses 2 bytes of memory (i.e.: 16 bits binary number)

  • int: uses 4 bytes of memory (i.e.: 32 bits binary number)

  • long: uses 8 bytes of memory (i.e.: 64 bits binary number)

 

Reminder:   the computer must store the integer (= whole) numbers as binary numbers

Storing integer (whole) values inside a computer program

How the computer store integers as fixed length binary numbers:

  • The (decimal) value 5 represented (= stored) as the byte data type is: 

       00000101

  • The (decimal) value 5 represented (= stored) as the short data type is: 

       0000000000000101

  • The (decimal) value 5 represented (= stored) as the int data type is: 

       00000000000000000000000000000101

So the leading zeros in a binary number is also stored in memory !!!

Quiz 1 - Applying what you have learned so far

  • What bit pattern is stored in memory variable x: 

           byte  x;

     x = 6;

Quiz 1 - Applying what you have learned so far

  • What bit pattern is stored in memory variable x: 

           byte  x;

     x = 6;

    Answer: 

         Convert 6 to binary:           6
                              2 ----- 0      
                                  3
                              2 ----- 1
                                  1
                              2 ----- 1
                                  0
   The binary number is:  110 binary
   Because x is a byte variable x contains: 00000110

Quiz 2 - Applying what you have learned so far

  • What bit pattern is stored in memory variable x: 

           int  x;

     x = 6;

Quiz 2 - Applying what you have learned so far

  • What bit pattern is stored in memory variable x: 

           int  x;

     x = 6;

    Answer: 

      
   The binary number is:  110 binary
   Because x is a int variable x contains:

      00000000000000000000000000000110       

   (32 bits)