- Just like 10s complement codes, there
are many different
2s complement codes -
depending on the
length (= number of bits)
of the code words
- Let's start with a
small
"Odometer code" using binary numbers.
This is the 3 bits (binary) "odometer" code:
Binary Odometer reading: 100 101 110 111 000 001 010 011 ----------------- +----+----+----+----+----+----+----+ Value represented: -4 -3 -2 -1 0 1 2 3
- Note:
- With 3 bits, we can represent only values between [-4 .. 3]
- With 3 bits, we can represent values between [-22 .. 22-1]
- Let's look at the
2s complement code
using one byte (= 8 bits):
2s comp Represented Code Value ======================== 10000000 -128 <--- smallest negative value with 8 bits (-27) 10000001 -127 ..... 11111000 -8 11111001 -7 11111010 -6 11111011 -5 11111100 -4 11111101 -3 11111110 -2 11111111 -1 00000000 0 00000001 1 00000010 2 00000011 3 00000100 4 00000101 5 00000110 6 00000111 7 00001000 8 ..... 01111111 127 <--- largest positive value with 8 bits (27-1)- With 8 bits, we can represent (= encode) the values between [-27, 27-1] = [-128, 127]
-
The mapping of the
representation to
the value that it represents
is based on
the following circular (modulo) addition:
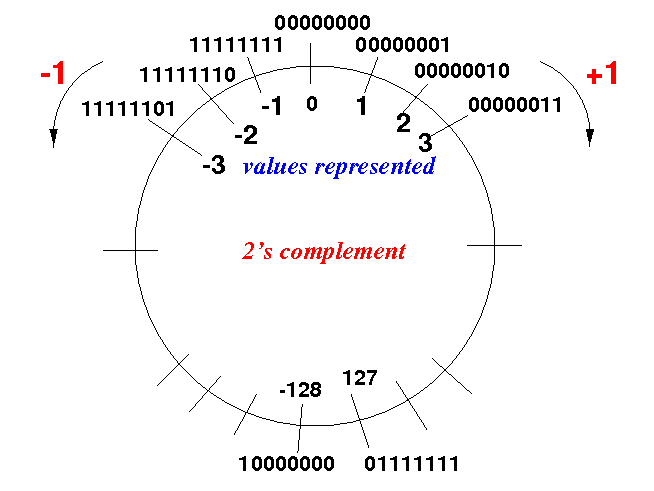
Property:
- If you move
clock-wise
on representation wheel,
you will add 1 to
the representation
- Therefore, the representation that you get by moving clock-wise must be 1 larger in value
- If you move
counter clock-wise
on representation wheel,
you will subtract 1 to
the representation
- Therefore, the representation that you get by moving counter clock-wise must be 1 larger in value
- If you move
clock-wise
on representation wheel,
you will add 1 to
the representation
- As I mentioned before,
to use a code effectively,
-- in this case the 2s complement code ---
you need to know how to convert a
value to 2s complement and vice versa
Let's see how we can encode a value in the 2s complement code
(Which is similar to the 10s complement example)
- Look at the following table carefully to discover the coding & decoding
method:
Absolute 2's compl Value Compare with: Value Binary number ================ ============================= 10000000 -128 128 10000000 10000001 -127 127 01111111 ..... 11111000 -8 8 00001000 11111001 -7 7 00000111 11111010 -6 6 00000110 11111011 -5 5 00000101 (11111011 = 100000000 - 00000101) 11111100 -4 4 00000100 11111101 -3 3 00000011 11111110 -2 2 00000010 11111111 -1 1 00000001 00000000 0 00000001 1 1 00000001 00000010 2 2 00000010 00000011 3 3 00000011 00000100 4 4 00000100 00000101 5 5 00000101 00000110 6 6 00000110 00000111 7 7 00000111 00001000 8 8 00001000 ..... 01111111 127 127 01111111
We see that:- When the value ≥ 0
(he bottom-half of the values):
- The 2s complement code
≡
binary number representation
(if we keep the leading 0's)
Example:
00000000 00000001 1 00000010 2 00000011 3 00000100 4 00000101 5 <----- Representation --------------- 00000101 -> 4 + 1 = 5 ^ ^ ^ | | 4 1
- The 2s complement code
≡
binary number representation
(if we keep the leading 0's)
- When the value < 0
(he top-half of the values):
2s complement code(value) = 10000000 − abs(value) in binary For the 8 bit 2s complement code
Example: how to find the 2s complement code for the value −5
2s compl Represented Absolute Binary code value value (abs(-5)) number of 5 --------------------------- ------------------------------- 11111011 -5 5 00000101 How to find the 2s compl code for -5: 100000000 - 00000101 ------------ 11111011 <---- 2s compl code for -5
Note:
- For a 16 bits
2s complement code, we will need to use
10000000000000000 in the
subtraction instead of
100000000
- For a 32 bits 2s complement code, we will need to use 100000000000000000000000000000000 in the subtraction instead of 100000000
Later in this webpage, I will show you a quicker way to handle the negative values....
- When the value ≥ 0
(he bottom-half of the values):
- First, observe that:
- When the left-most bit of the
2s complement code = 0:
- The code word represents a positive value (or 0)
- When the left-most bit of the
2s complement code = 1:
- The code word represents a negative value
- When the left-most bit of the
2s complement code = 0:
- Converting a
2's complement code c
to its signed value:
- If the
2s complement code
c begins with
0 bit (= positive value or 0):
- Use the
formula:
(see: click here)
dn×2n + dn-1×2n-1 ... + d1×21 + d0×20
to find the (decimal) value reprsented by the 2s complement code
- Use the
formula:
(see: click here)
- If the
2s complement code
c begins with
1 bit (= negative value):
Represented value in binary = - ( 100000000 - c )
Example:
2s complement code c = 00010010 What value does this code represent ? 00010010 -> it is a positive value the value = 00010010 in binary Convert to decimal: 0 0 0 1 0 0 1 0 16 + 2 = 18 Value = 18
2s complement code c = 11101110 What value does this code represent ? 11101110 -> it is a negative number... (1) Compute: 100000000 - 11101110 ----------- 00010010 (2) the absolute value of the negative value is equal to 00010010 (binary), which is equal to 18 (decimal) (3) Since the value is negative, the value represented by 11101110 is: -18 ! - If the
2s complement code
c begins with
0 bit (= positive value or 0):
- We have seen 2 examples above
on encoding and decoding
values in
the 2s complement code
Here is a summary of the examples:
2s complement code Value represented by the code -------------------- ------------------------------- 00000111 7 11111001 -7 00010010 18 11101110 -18Can you see the how the representation for x and −x are related ??
Take a close look at this table with more representations of positive and negative values:
Absolute 2's compl Value Compare with: Value Binary number ================ ============================= 10000000 -128 128 10000000 10000001 -127 127 01111111 ..... 11111000 -8 8 00001000 11111001 -7 7 00000111 11111010 -6 6 00000110 11111011 -5 5 00000101 (11111011 = 100000000 - 00000101) 11111100 -4 4 00000100 11111101 -3 3 00000011 11111110 -2 2 00000010 11111111 -1 1 00000001 00000000 0 00000001 1 1 00000001 00000010 2 2 00000010 00000011 3 3 00000011 00000100 4 4 00000100 00000101 5 5 00000101 00000110 6 6 00000110 00000111 7 7 00000111 00001000 8 8 00001000 ..... 01111111 127 127 01111111You can notice the following relationship between the representations for x and -x:
2s compl code(-x) = 10000000 - 2s complement code(x)
Example: 2s compl code for -5 = 10000000 - 2s compl code for 5 100000000 - 00000101 ----------- 11111011
So to negate a value represented in the 2s complement code:
- You must subtract the 2s complement code
from 1000...000
(I use ... in the number, because:
- To negate a 8 bits 2s complement code, you must subtract from 100000000
- To negate a 16 bits 2s complement code, you must subtract from 10000000000000000
- To negate a 32 bits 2s complement code, you must subtract from 100000000000000000000000000000000
- You must subtract the 2s complement code
from 1000...000
- In high school,
you may have learned an easier way
to negate a 2s complement code.
What you may have learned is:
- Flip the bits in the binary number
- Add 1 to the result
You probably have no idea why this works...
Let me explain this procedure using an example...
The binary representation for the value 7 in 8 bits is:
00000111 (= 7)To find the 2s complement representation for −7, we subtract 00000111 from 100000000:
100000000 - 00000111 (= 7) ----------- 11111001 (= -7)The subtraction can be broken up in 2 steps as follows:
100000000 - 00000111 = (1 + 11111111) - 00000111 = 1 + (11111111 - 00000111) [easy subtraction !] = 1 + 11111000 [result is same as flipping bits !]
Subtraction using 11111111 will result in flipping the bits in the other binary number because you never have to borrow and 1 - 0 = 1 and 1 - 1 = 0 !!!
Summary: to negate a 2s complement representation:
- Flip every bit in the 2s complement representation
- Add 1 to the result
Another example:
As you saw above: 00010010 represents +18 To get the representation for -18, you can do this: (1) Flip each bit: 00010010 -> 11101101 (2) Add 1 to result: 11101101 + 1 ---------- 11101110 which is - as you saw above - the representation for -18
- The 2s complement encoding has
the following
"nice" properties:
- There is only one representation
for the value ZERO (check for yourself)
- Arithmetic operations using 2s compliment code are "natural" (i.e., you don't need to worry about negative numbers when you add) - see examples below
- There is only one representation
for the value ZERO (check for yourself)
- Adding 2's complement numbers:
Values 8 digit 2's compl repr Adding 2 positive 5 00000101 values + 9 + 00001001 ----- ---------- 14 00001110 -> 8 + 4 + 2 = 14 Adding positive + 5 00000101 negative + -9 + 11110111 ----- ---------- -4 11111100 -> represents -4 Adding negative + -5 11111011 positive + 9 + 00001001 ----- ---------- 4 00000100 -> represents 4 Adding 2 negative -5 11111011 values + -9 + 11110111 ----- ---------- -14 11110010 -> represents -14 - Subtracting 2's complement numbers:
Values 8 digit 2's compl repr Subtract 2 positive 5 00000101 values - 9 - 00001001 ----- ---------- -4 11111100 -> represents -4 Subtract positive - 5 00000101 negative - -9 - 11110111 ----- ---------- 14 00001110 -> represents 14 Subtract negative - -5 11111011 positive - 9 - 00001001 ----- ---------- -14 11110010 -> represents -14 Subtract 2 negative -5 11111011 values - -9 - 11110111 ----- ---------- 4 00000100 -> represents 4
- Example Program:
(Demo above code)

- Prog file: /home/cs255001/demo/Java/ShowIntTypes.java
How to run the program:
- To compile: javac ShowIntTypes.java
- To run: java ShowIntTypes
- What is "overflow":
- Using 8 bits, we can represent the binary values between -128 and 127
- Computer operation manipulate (change) the representation
For example:
00000011 <---- representation for the value *** (3) + 00000101 <---- representation for the value ***** (5) ------------ 00001000 <---- representation for the value ******** (8) - When the result of some operation on byte representations
falls outside this range, then the value that
is represented by the result is different from
the correct value.
- This phenomenon is called overflow
- Overflow is a part of our daily life now that the computer is an integral part of our society and you should be aware of this phenomenon so you do not get caught by surprise...
- Using 8 bits, we can represent the binary values between -128 and 127
- Here is a program that demonstrates the overflow phenomenon:
click here
DEMO
- Try entering 1 + 1
- and then: 127 + 1 (this will cause an overflow)
- Do you understand why there is overflow at 127 using byte variables ??
- The following program is the same as the previous one, except I have
added a function to print out the binary representation
of the values.
You can use this program to see why the program prints certain results: click here DEMO
- Computer can manipluate integers of various lengths:
- 8 bits (byte type in Java, char type in C, C++)
- 16 bits (short type in Java, C and C++)
- 32 bits (int type in Java, C and C++)
- 64 bits (long type in Java, C and C++)
- 128 bits (long long type in C and C++)
- This program shows the effect of using more bits: click here DEMO
- Other types of variables also have
overflow problems, just later...
- short type variables will overflow at around 32000 (215)
- int type variables overflow at around 2 billion (231)
- Use the previous demo program to verify.
- Example Program:
(Demo above code)

- Prog file: /home/cs255001/demo/Java/ShowByteAdd.java
How to run the program:
- To compile: javac ShowByteAdd.java
- To run: java ShowByteAdd
Overflow
- Overflow has
nothing to do with
the 2s complement representation
You can use any code, and you will still have the overflow problem....
Because...
- The reason that you
cannot represent
some result is because:
- We are using a finite number
bytes to
represent the values !!!
Since the set of possible values in computations are infinite, you will not be able to represent some result (that are too large !!!)
So please don't blame the 2s complement code for the overflow phenomenon....
Blame it on the fact that we use 4 bytes to store an int typed variable !!!
- We are using a finite number
bytes to
represent the values !!!