(Detailed) structure of the (computer) memory

Computer memory consists of series of memory "cells":

One memory cell is called a byte
Each byte is identified by a binary number called the (memory) address
(An address is usually written as a decimal number for convenience)

(Detailed) structure of the (computer) memory - Example memory content

Each memory byte can store a 8 bit pattern (= a pattern consisting of 8 binary bits)
Example of what is stored inside the computer memory:

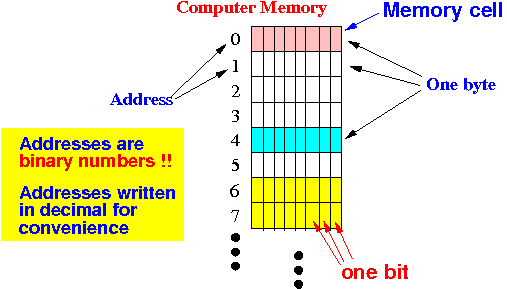
Example: the byte at address 0 contains the binary number 00000101

All the different binary numbers that can be stored in a 1 byte memory

One (1) byte can store one of these 256 different binary numbers:

00000000 00000001 00000010 00000011 00000100 00000101 00000110 00000111 00001000 00001001 00001010 00001011 00001100 00001101 00001110 00001111 00010000 00010001 00010010 00010011 00010100 00010101 00010110 00010111 00011000 00011001 00011010 00011011 00011100 00011101 00011110 00011111 00100000 00100001 00100010 00100011 00100100 00100101 00100110 00100111 00101000 00101001 00101010 00101011 00101100 00101101 00101110 00101111 00110000 00110001 00110010 00110011 00110100 00110101 00110110 00110111 00111000 00111001 00111010 00111011 00111100 00111101 00111110 00111111 .... (And so on... - too many to list them all out)

All the different binary numbers that can be stored in a 1 byte memory

One (1) byte can store one of these 256 different binary numbers:

00000000 00000001 00000010 00000011 00000100 00000101 00000110 00000111 00001000 00001001 00001010 00001011 00001100 00001101 00001110 00001111 00010000 00010001 00010010 00010011 00010100 00010101 00010110 00010111 00011000 00011001 00011010 00011011 00011100 00011101 00011110 00011111 00100000 00100001 00100010 00100011 00100100 00100101 00100110 00100111 00101000 00101001 00101010 00101011 00101100 00101101 00101110 00101111 00110000 00110001 00110010 00110011 00110100 00110101 00110110 00110111 00111000 00111001 00111010 00111011 00111100 00111101 00111110 00111111 .... (And so on... - too many to list them all out)

Each binary number will represent exactly 1 numeric value
(e.g.: 00000000 = zero (0), 00000001 = one (1), and so on.)

All the different binary numbers that can be stored in a 1 byte memory

One (1) byte can store one of these 256 different binary numbers:

00000000 00000001 00000010 00000011 00000100 00000101 00000110 00000111 00001000 00001001 00001010 00001011 00001100 00001101 00001110 00001111 00010000 00010001 00010010 00010011 00010100 00010101 00010110 00010111 00011000 00011001 00011010 00011011 00011100 00011101 00011110 00011111 00100000 00100001 00100010 00100011 00100100 00100101 00100110 00100111 00101000 00101001 00101010 00101011 00101100 00101101 00101110 00101111 00110000 00110001 00110010 00110011 00110100 00110101 00110110 00110111 00111000 00111001 00111010 00111011 00111100 00111101 00111110 00111111 .... (And so on... - too many to list them all out)

Each binary number will represent exactly 1 numeric value
(e.g.: 00000000 = zero (0), 00000001 = one (1), and so on.)

Therefore:

One (1) byte (of memory) can store one of 256 different possible numeric values
E.g.: 0, 1, 2, 3, ..., 255

All the different binary numbers that can be stored in a 1 byte memory

One (1) byte can store one of these 256 different binary numbers:

00000000 00000001 00000010 00000011 00000100 00000101 00000110 00000111 00001000 00001001 00001010 00001011 00001100 00001101 00001110 00001111 00010000 00010001 00010010 00010011 00010100 00010101 00010110 00010111 00011000 00011001 00011010 00011011 00011100 00011101 00011110 00011111 00100000 00100001 00100010 00100011 00100100 00100101 00100110 00100111 00101000 00101001 00101010 00101011 00101100 00101101 00101110 00101111 00110000 00110001 00110010 00110011 00110100 00110101 00110110 00110111 00111000 00111001 00111010 00111011 00111100 00111101 00111110 00111111 .... (And so on... - too many to list them all out)

Each binary number will represent exactly 1 numeric value
(e.g.: 00000000 = zero (0), 00000001 = one (1), and so on.)

However:

Many computer programs need to use much larger numbers !!!
E.g.: 1000 ( > 255)

All the different binary numbers that can be stored in a 1 byte memory

Solution:

The memory (RAM) has the capability to combine a number of adjacent memory bytes to represent larger values (with some limitations) !!!

Example: Combining two (2) adjacent bytes creates a cell of 16 bits that can store one of 2¹⁶ different binary numbers:

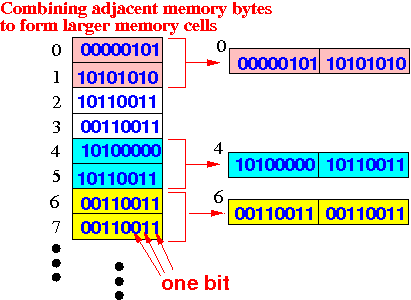
Each pair of adjacent bytes can store one larger 16 bits binary number

Combining 2 adjacent memory bytes (cells) - analogy

Consider 2 adjacent box - each box contains a small sheet of paper with a 2 digits (decimal) number:

You can interpret the values on the papers in different ways:

The box at 1600 stores the value 86 and
The box at 1601 stores the value 49
The (combined) box at 1600 stores the value 8649
(You can store/represent larger values (= more digits) using a combined box )

Limitation on combining 2 adjacent memory bytes (cells)

Due to the way that computer memory is constructed, the computer system imposes this restriction:

Two adjacent memory cells can be combined into a 16 bits memory cell if :
the first memory cell has an even address

Example:

Example: cells at address 0, 1 can be combined into a 16 bit memory cell with address 0
Example: cells at address 4, 5 can be combined into a 16 bit memory cell with address 4
Example: cells at address 5, 6 cannot be combined !! (because address 5 is odd)

Application of combining 2 adjacent memory cells

When a pair of adjacent memory cells are combined, the larger memory cell can store 2¹⁶ = 65536 different patterns

Each pattern is used to represent a unique value

Example application:

A short typed variable in Java is stored in a pair of memory cells
That's why you can store the values -32768 .. 32767 (65536 different values) in a short typed variable
See: click here

Constraint on placement of short typed variables:
Variables of the type short must start at an even memory address

Combining 4 adjacent memory bytes (cells)

Combining 4 consecutive memory cells:

4 consecutive memory bytes can be combined into a 32 bits memory cell
Alignment restriction imposed:

Example:

Application of combining 4 consecutive memory bytes

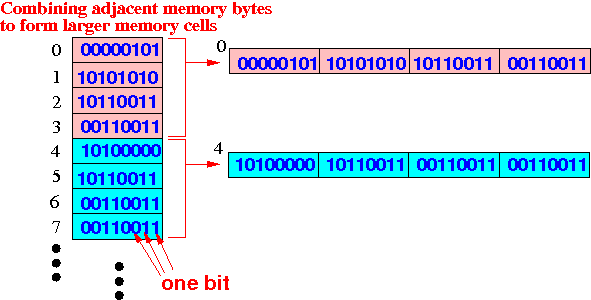
Example where the computer will combine 4 consecutive memory bytes:

A int typed variable in Java is stored in a 4 consecutive memory bytes
Each quartet (group of 4) of memory cells can store 2³² = 4294967296 different patterns
That's why you can store the values -2147483648 .. 2147483647 (4294967296 different values) in a int typed variable
See: click here
Constraint on placement of int typed variables:
Variables of the type int must start at an memory address that is divisble by 4

DEMO: demo/Alignment/align.c

Postscript

Computer memory can also combine 8 consecutive bytes
Limitation:
Program variables of the data types double and long are stored in 8 consecutive memory bytes
Constraint on placement of double/long typed variables:
Variables of the type double/long must start at an memory address that is divisble by 8
In general, the computer memory only allow combining 2ⁿ bytes (exact power of 2) of consecutive memory cells