Recursion is a
divide-and-conquer
problem solving technique
|
When can we use
recursion ?
Suppose we need to solve some problem of size n:
When can we use
recursion ?
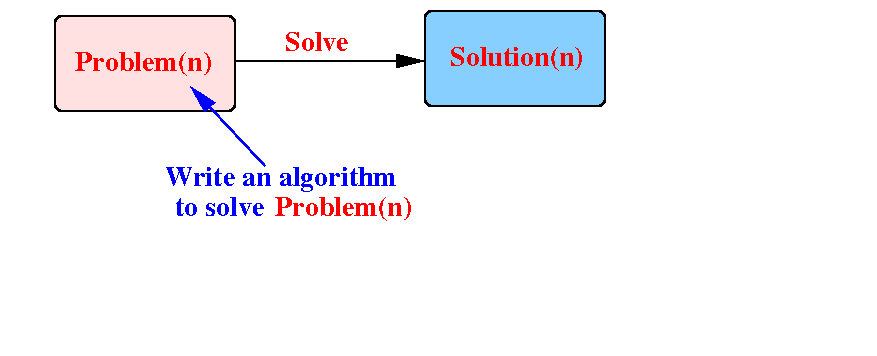
Consider the other identical (but) smaller problems:
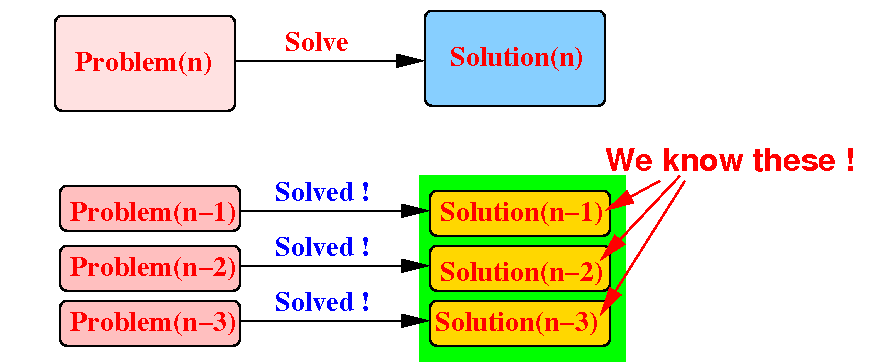
Suppose that we (already) have the solutions for all the smaller problems, i.e.: we do not need to solve them
When can we use
recursion ?
If we can use the solutions of the smaller problems to find Solution(n):
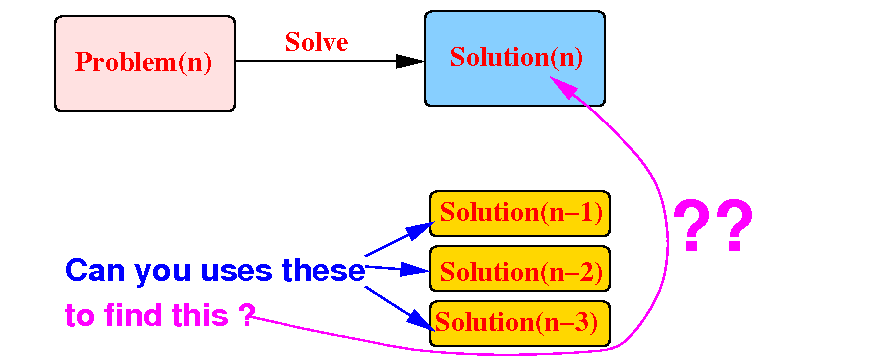
Then: we can use recursion to solve the Problem(n)
The difficulty
in using
recursion
The main difficulty of using recursion is to find a way to use the smaller solutions to find Solution(n):
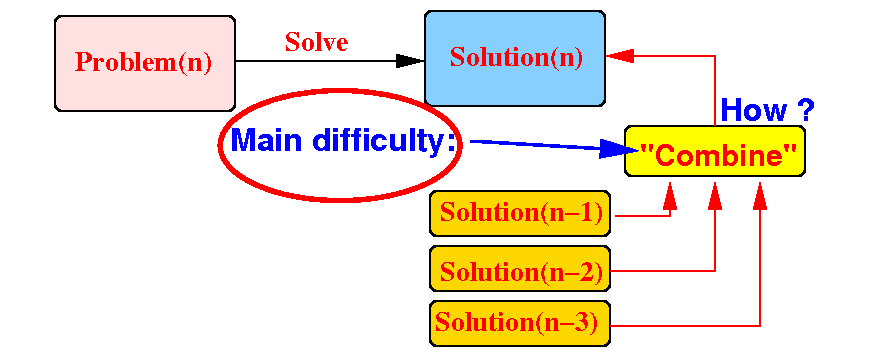
This step is problem-dependent !
Example: why we can use
recursion to compute the
factorial function
Suppose we need to compute factorial(10):
Recursion = a divide and conquer algorithm
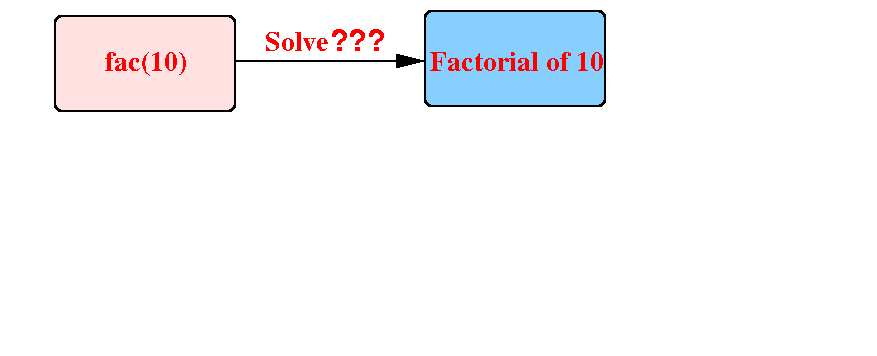
Consider the smaller problem of factorial(9):
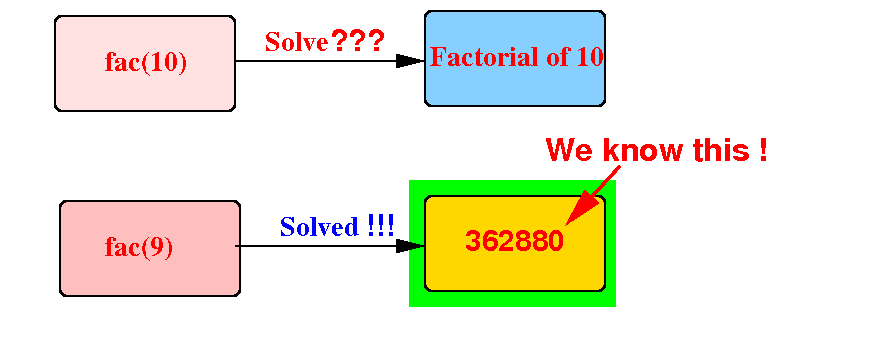
Question: can we solve factorial(10) using the value 362880 ?
Recursion = a divide and conquer algorithm
We can compute factorial(10) using the value 362880 as follows:
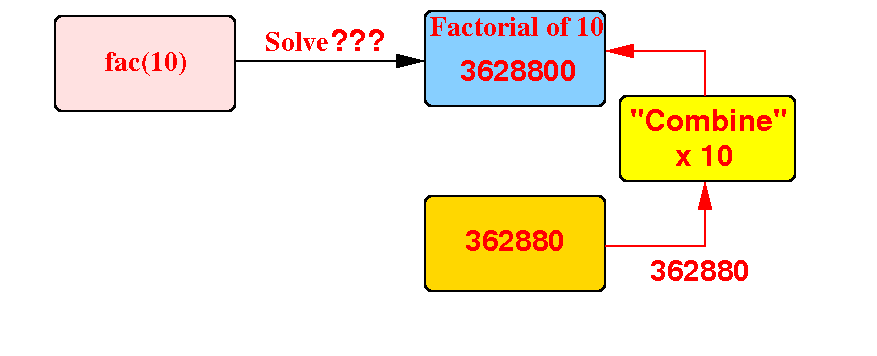
Therefore: we can write factorial as a recursive function !
The factorial( ) function
revisited
Traditionally, the factorial(int n) method is defined a follows:
public static int factorial(int n)
{
// computes n!
if ( n == 0 )
return 1;
else
return n * factorial(n-1);
}
|
This form does not reveal how the divide-and-conquer technique was used...
The factorial( ) function
revisited
How I like to write factorial( ) as a divide-and-conquer algorithm:
int factorial(int n)
{
}
|
Let's write the factorial( ) method again, but this time using the divide-and-conquer principle
The factorial( ) function
revisited
The base case(s) is when the problem is easy enough that I solve it myself:
int factorial(int n)
{
if ( n == 0 )
return 1; // Base case
}
|
In the divide step, we let someone else solve a smaller problem
The factorial( ) function
revisited
Let someone else solve a smaller problem that I can use to solve my problem:
int factorial(int n)
{
int helpSol; // Solution to the smaller problem
if ( n == 0 )
return 1; // Base case
else
{
helpSol = factorial(n-1); // Tell someone to solve this
// (We receive the solution in helpSol)
}
}
|
In the conquer step, we use helpSol to find solution for the original problem
The factorial( ) function
revisited
We solve factorial(n) using helpSol like this:
int factorial(int n)
{
int helpSol; // Solution to the smaller problem
int mySol; // Solution to my problem
if ( n == 0 )
return 1; // Base case
else
{
helpSol = factorial(n-1); // Tell someone to solve this
// (We receive the solution in helpSol)
mySol = n*helpSol; // Solve my problem using the
// solution of the smaller problem
}
}
|
Finally, we return the solution...
The factorial( ) function
revisited
The factorial(n) method written as a divide-and-conquer algorithm:
int factorial(int n)
{
int helpSol; // Solution to the smaller problem
int mySol; // Solution to my problem
if ( n == 0 )
return 1; // Base case
else
{
helpSol = factorial(n-1); // Tell someone to solve this
// (We receive the solution in helpSol)
mySol = n*helpSol; // Solve my problem using the
// solution of the smaller problem
return(mySol);
}
}
|
Important insight
to help you
understand and write recursive
functions
You must distinguish between (1) the factorial( ) function that solves your problem and (2) the factorial( ) function that solves a smaller problem(s):
int factorial(int n) <--- This factorial( ) represents "YOU" { int helpSol; int mySol; if ( n == 0 ) return 1; else { helpSol = factorial(n-1); <--- This factorial( ) your "helper" ! // This factorial( ) solves a smaller problem mySol = n*helpSol; return (mySol); } } |
They are 2 different factorial( ) functions !
So recursion will run another (copy of the) function