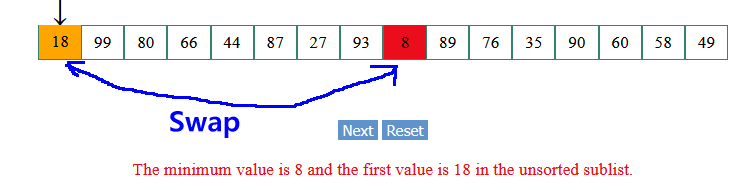
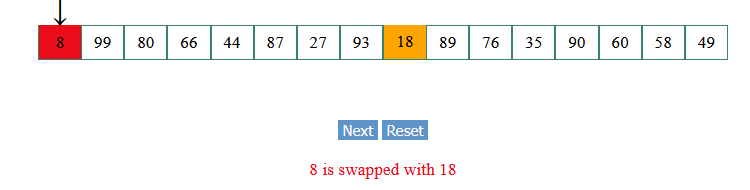
The selection sort algorithm

  • The selection sort algorithm:

      • Selection sort finds the smallest number in the list and swaps it with the first element.

            

      • It then finds the smallest number remaining and swaps it with the second element

      • And so on, until only a single number remains (= the last number in the list).

  • Check out the animation:

The selection sort algorithm

  • The selection sort algorithm:

      • Selection sort finds the smallest number in the list and swaps it with the first element.

            

      • It then finds the smallest number remaining and swaps it with the second element

      • And so on, until only a single number remains (= the last number in the list).

  • Check out the animation:

The selection sort algorithm

  • The selection sort algorithm:

      • Selection sort finds the smallest number in the list and swaps it with the first element.

            

      • It then finds the smallest number remaining and swaps it with the second element

      • And so on, until only a single number remains (= the last number in the list).

  • Check out the animation:

The selection sort algorithm

  • The selection sort algorithm:

      • Selection sort finds the smallest number in the list and swaps it with the first element.

      • It then finds the smallest number remaining and swaps it with the second element

            

      • And so on, until only a single number remains (= the last number in the list).

  • Check out the animation:

The selection sort algorithm

  • The selection sort algorithm:

      • Selection sort finds the smallest number in the list and swaps it with the first element.

      • It then finds the smallest number remaining and swaps it with the second element

            

      • And so on, until only a single number remains (= the last number in the list).

  • Check out the animation:

The selection sort algorithm 

    void selectionSort(double list[], int N) 
    {
        for (int k = 0; k < N-1; k++)
        {
            // Find the minimum value and its index in list[k..N-1]
            double min = list[k];    // Assume first element is min
            int    indexOfMin = k;   // Index of current min
    
            for ( int i = k+1; i < N; i++ )
                if ( list[i] < min ) // We found a smaller element
                {
                    min = list[i];   // Update min value
                    indexOfMin = i;  // Update its index in array
                }
    
            // Swap list[k] with list[indexOfMin] if necessary
            if ( indexOfMin != k )
            {   // Swap list[indexOfMin] and list[k]
                double help = list[indexOfMin];
                list[indexOfMin] = list[k];
                list[k] = help;
            }
        } 
    }

The selection sort algorithm 

    void selectionSort(double list[], int N) 
    {
        for (int k = 0; k < N-1; k++)
        {
            // Find the minimum value and its index in list[k..N-1]
            double min = list[k];    // Assume first element is min
            int    indexOfMin = k;   // Index of current min

            for ( int i = k+1; i < N; i++ )
                if ( list[i] < min ) // We found a smaller element
                {
                    min = list[i];   // Update min value
                    indexOfMin = i;  // Update its index in array
                }
    
            // Swap list[k] with list[indexOfMin] if necessary
            if ( indexOfMin != k )
            {   // Swap list[indexOfMin] and list[k]
                double help = list[indexOfMin];
                list[indexOfMin] = list[k];
                list[k] = help;
            }
        } 
    }

The selection sort algorithm 

    void selectionSort(double list[], int N) 
    {
        for (int k = 0; k < N-1; k++)
        {
            // Find the minimum value and its index in list[k..N-1]
            double min = list[k];    // Assume first element is min
            int    indexOfMin = k;   // Index of current min

            for ( int i = k+1; i < N; i++ )
                if ( list[i] < min ) // We found a smaller element
                {
                    min = list[i];   // Update min value
                    indexOfMin = i;  // Update its index in array
                }
   
            // Swap list[k] with list[indexOfMin] if necessary
            if ( indexOfMin != k )
            {   // Swap list[indexOfMin] and list[k]
                double help = list[indexOfMin];
                list[indexOfMin] = list[k];
                list[k] = help;
            }
        } 
    }

The selection sort algorithm 

    void selectionSort(double list[], int N) 
    {
        for (int k = 0; k < N-1; k++)
        {
            // Find the minimum value and its index in list[k..N-1]
            double min = list[k];    // Assume first element is min
            int    indexOfMin = k;   // Index of current min

            for ( int i = k+1; i < N; i++ )
                if ( list[i] < min ) // We found a smaller element
                {
                    min = list[i];   // Update min value
                    indexOfMin = i;  // Update its index in array
                }
   
            // Swap list[k] with list[indexOfMin] if necessary
            if ( indexOfMin != k )
            {   // Swap list[indexOfMin] and list[k]
                double help = list[indexOfMin];
                list[indexOfMin] = list[k];
                list[k] = help;
            }
        } 
    }

The selection sort algorithm 

    void selectionSort(double list[], int N) 
    {
        for (int k = 0; k < N-1; k++)
        {
            // Find the minimum value and its index in list[k..N-1]
            double min = list[k];    // Assume first element is min
            int    indexOfMin = k;   // Index of current min

            for ( int i = k+1; i < N; i++ )
                if ( list[i] < min ) // We found a smaller element
                {
                    min = list[i];   // Update min value
                    indexOfMin = i;  // Update its index in array
                }
   
            // Swap list[k] with list[indexOfMin] if necessary
            if ( indexOfMin != k )
            {   // Swap list[indexOfMin] and list[k]
                double help = list[indexOfMin];
                list[indexOfMin] = list[k];
                list[k] = help;
            }
        } 
    }

DEMO: demo/C/set1/selectionSort.c