- Recall that:
- An AVL tree is
a height-balanced
Binary Search Tree
In fact: an AVL tree is a BST !!!
We will first discuss how to maintain height information in a BST before we discuss AVL trees
- An AVL tree is
a height-balanced
Binary Search Tree
- Height information:
- In order to find out whether the BST is heigh balanced, each node in the tree must maintain height information
- Data structure used to represent a
node in a "height-aware" BST:
public class BSTEntry { public String key; // Key public Integer value; // Value public int height; // Height information public BSTEntry parent; public BSTEntry left; public BSTEntry right; }
- Example Program:
(Demo above code)

- The new BSTEntry.java Prog file: click here
- Observation:
Leaf node: Height( leaf node ) = 1
Non-leaf node n: Height( n ) = max ( height(n.left) , height(n.right) ) + 1
Example:
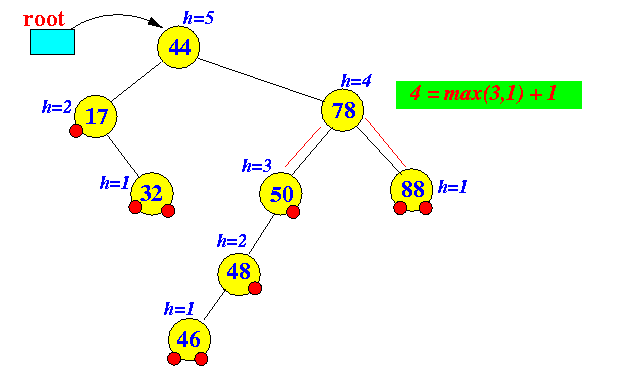
- Height of a
newly inserted node:
- The height of a
newly inserted node
is always equal to
1
Because:
-
A node is always
inserted as a leaf node
(and leaf nodes has
height = 1)
Example:
Tree before insert operation Tree after insert operation 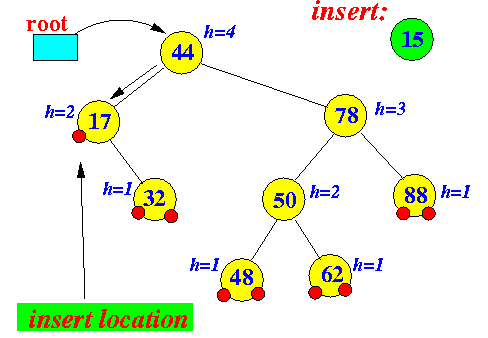
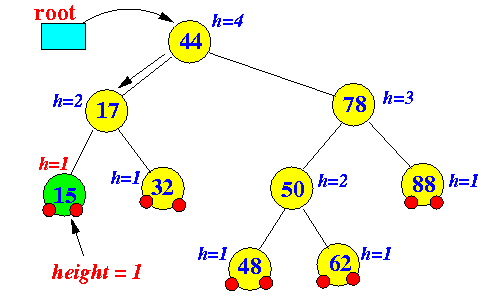
-
A node is always
inserted as a leaf node
(and leaf nodes has
height = 1)
- The height of a
newly inserted node
is always equal to
1
- Facts:
- The height of
some nodes in the BST
may increase in an
insert operation
- The height of some nodes in the BST can may decrease in an delete operation
- The height of
some nodes in the BST
may increase in an
insert operation
- Example: an
insert operation that
does not
increase the height of any node in a BST
Tree before insert operation Tree after insert operation 
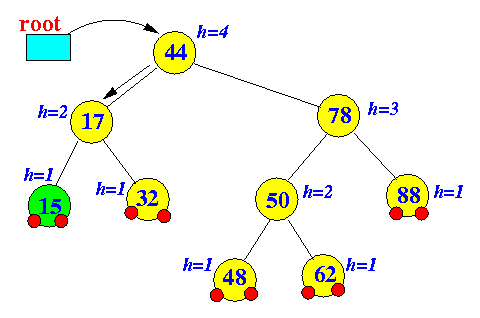
- Example: an
insert operation that
increases
the height of some nodes in a BST
Tree before insert operation Tree after insert operation 
- Example: an
delete operation that
does not
decrease the height of any node in a BST
Tree before delete operation Tree after delete operation 

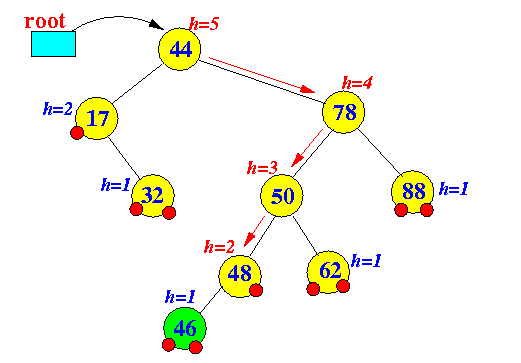
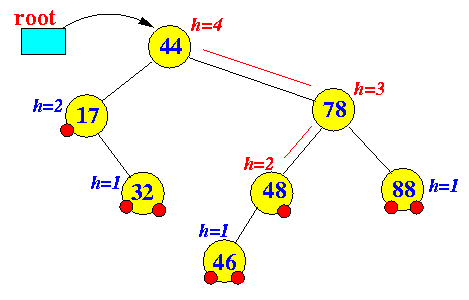
- Example: an
delete operation that
decreases
the height of some nodes in a BST
Tree before delete operation Tree after delete operation 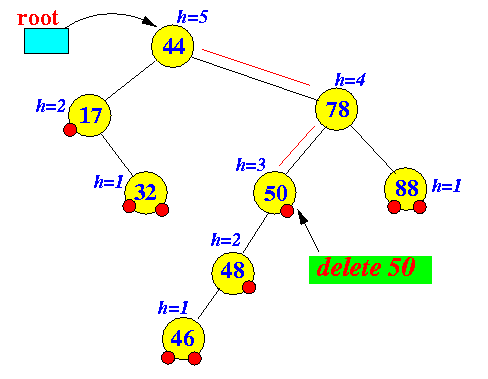
- Prelude to
maintaining the height information
in a "height-aware" BST:
- Fact:
- We must update the height information of some nodes when we insert a node or remove a node from a BST/AVL tree
- Naive solution:
- Recompute the height information of every node in the tree when we perform an insert/delete operation.
This is a bad solution because the height information of most of the nodes did not change !!!
- Smarter solution:
- Find out
which of the nodes
may be affected
by the
insert/delete operation !!!
- And recompute the height information of these nodes only !!!
- Find out
which of the nodes
may be affected
by the
insert/delete operation !!!
- Fact:
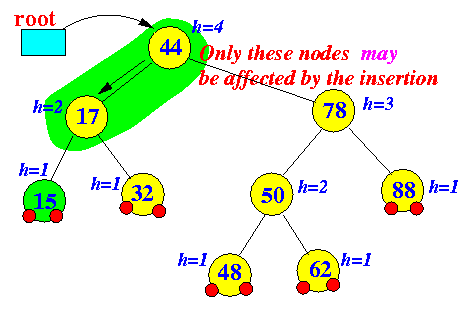
- Observation:
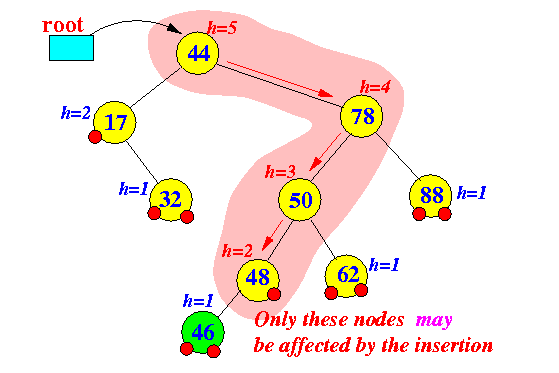
- Only nodes that are on the path between the root node and the inserted/deleted node are affected by the inserted/deleted operation
- Example: insert
Tree before insert operation Tree after insert operation 

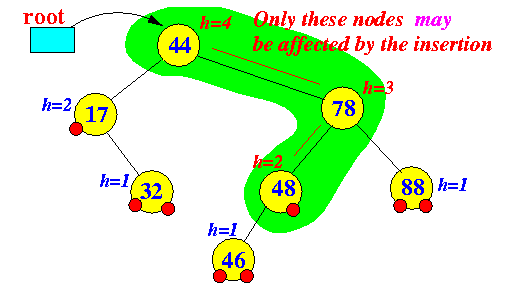
- Example: delete
Tree before delete operation Tree after delete operation 


- Conclusion:
- When a node is
inserted/deleted,
we
only
need to
update the height information
of
the node and all its parent
nodes
(all parent nodes = the parent node, the parent's parent, and so on.... all the way to the root node)
- When a node is
inserted/deleted,
we
only
need to
update the height information
of
the node and all its parent
nodes
- Armed with
the knowledge that:
- We only need to update the height information of the node and all its parent nodes
we can write the following recompHeight() method:
/* ================================================================ recompHeight(x): recompute height starting at x (and up) ================================================================ */ public static void recompHeight( BSTEntry x ) { while ( x != null ) { x.height = maxHeight( x.left, x.right ) + 1; // Compute height for x x = x.parent; // Go to the parent node } }
- Very important:
- The height recomputation algorithm
must be executed
starting at the
parent node of
the
physically inserted/deleted node
- Definition:
- The action location of the insert/delete operation = the node in the BST that was physically inserted/removed.
- The height recomputation algorithm
must be executed
starting at the
parent node of
the
physically inserted/deleted node
- Example 1:
- Initial BST:

- After deleting
the node 50 and
before
recomputing the heights of the nodes:

- Recompute height information:
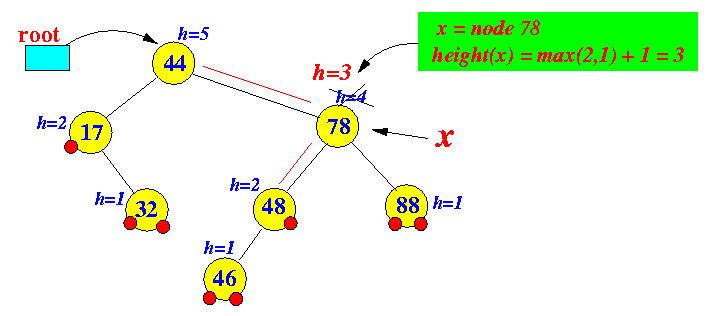
- Start
at the parent node
of the action location
(I.e., start at x = node 78 because the "action" location was a child node of 78)
- Continue
go up in the tree:
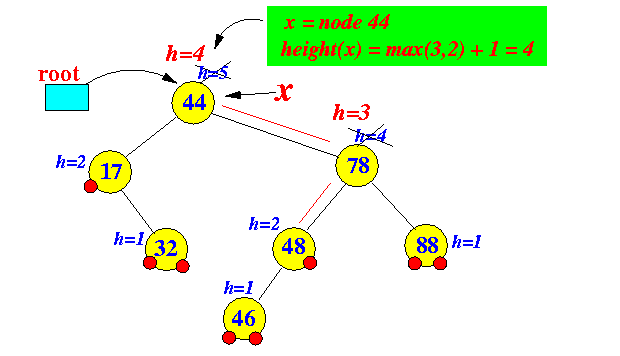
- Done (all heights are now correct !)
- Start
at the parent node
of the action location
- Initial BST:
- Example 2: notice the
action location !!!
- Initial BST:

- After deleting
the node 50 and
before
recomputing the heights of the nodes:
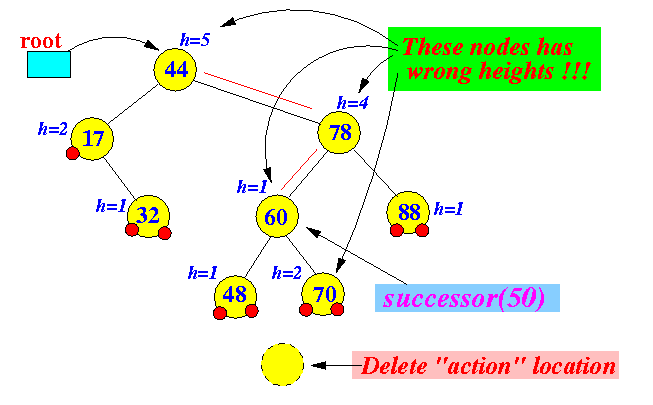
Notice that:
- The node that
was physically removed
is a
child node of 70
- Therefore:
- Node 70 is the parent node of the action location !!!
- The node that
was physically removed
is a
child node of 70
- Recompute height information:
- Start
at the parent node
of the action location
(I.e., start at x = node 70 because the "action" location was a child node of 70)
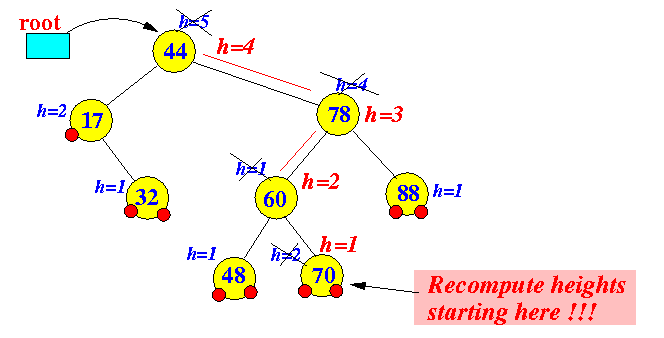
- Note: all heights are now correct !
- Start
at the parent node
of the action location
- Initial BST:
- Modified
put() method that
manages height information:
public void put(String k, Integer v) { BSTEntry p; // Help variable /* ---------------------------------------------------------- Just like linked list, insert in an EMPTY BST must be taken care off separately by an if-statement ---------------------------------------------------------- */ if ( root == null ) { // Insert into an empty BST root = new BSTEntry( k, v ); root.height = 1; return; } /* -------------------------------------------- Find the node with key == "key" in the BST -------------------------------------------- */ p = findEntry(k); if ( k.equals( p.key ) ) { p.value = v; // Update value return; } /* -------------------------------------------- Insert a new entry (k,v) under p !!! -------------------------------------------- */ BSTEntry q = new BSTEntry( k, v ); q.height = 1; q.parent = p; /* ************************************************* Upto here, it's just the OLD put() method ************************************************* */ /* --------------------------------------------------- Action location = q The parent of q = q So: recompute the height of all nodes starting at p --------------------------------------------------- */ recompHeight(p); }
- Modified
put() method that
manages height information:
public void remove(String k) { BSTEntry p, q; // Help variables BSTEntry parent; // parent node BSTEntry succ; // successor node /* -------------------------------------------- Find the node with key == "key" in the BST -------------------------------------------- */ p = findEntry(k); if ( ! k.equals( p.key ) ) return; // Not found ==> nothing to delete.... /* ======================================================== Hibbard's Algorithm ======================================================== */ if ( p.left == null && p.right == null ) // Case 0: p has no children { parent = p.parent; /* -------------------------------- Delete p from p's parent -------------------------------- */ if ( parent.left == p ) parent.left = null; else parent.right = null; /* -------------------------------------------- parent = parent of the deleted node Recompute height starting at "parent"... -------------------------------------------- */ recompHeight( parent ); return; } if ( p.left == null ) // Case 1a: p has 1 (right) child { parent = p.parent; /* ---------------------------------------------- Link p's right child as p's parent child ---------------------------------------------- */ if ( parent.left == p ) parent.left = p.right; else parent.right = p.right; /* -------------------------------------------- parent = parent of the deleted node Recompute height starting at "parent"... -------------------------------------------- */ recompHeight( parent ); return; } if ( p.right== null ) // Case 1b: p has 1 (left) child { parent = p.parent; /* ---------------------------------------------- Link p's left child as p's parent child ---------------------------------------------- */ if ( parent.left == p ) parent.left = p.left; else parent.right = p.left; /* -------------------------------------------- parent = parent of the deleted node Recompute height starting at "parent"... -------------------------------------------- */ recompHeight( parent ); return; } /* ================================================================ Tough case: node has 2 children - find successor of p succ(p) is as as follows: 1 step right, all the way left Note: succ(p) has NOT left child ! ================================================================ */ succ = p.right; // p has 2 children.... while ( succ.left != null ) succ = succ.left; p.key = succ.key; // Replace p with successor p.value = succ.value; /* -------------------------------- Delete succ from succ's parent -------------------------------- */ parent = succ.parent; if ( parent.left == succ ) parent.left = succ.right; // parent skip over succ ... else parent.right = succ.right; // ... and point to succ's right child /* -------------------------------------------- parent = parent of the deleted node Recompute height starting at "parent"... -------------------------------------------- */ recompHeight( parent ); return; }
- Example Program:
(Demo above code)

- The BSTEntry.java Prog file: click here
- The BST.java
(with height maintenance) Prog file:
click here
- A test program: click here
How to run the program:
- Right click on link(s) and
save in a scratch directory
- To compile: javac TestBST.java
- To run: java TestBST
Output:
[lion,9999](h=1) ================================ [lion,9999](h=2) [dog,1000](h=1) ================================ [lion,9999](h=3)* [dog,1000](h=2) [cat,500](h=1) ================================ [tiger,8888](h=1) [lion,9999](h=3) [dog,1000](h=2) [cat,500](h=1) ================================ [tiger,8888](h=1) [lion,9999](h=3) [horse,2000](h=1) [dog,1000](h=2) [cat,500](h=1) ================================ [tiger,8888](h=1) [lion,9999](h=4)* [horse,2000](h=1) [dog,1000](h=3) [cat,500](h=2) [ape,1500](h=1)