---

The (2,4)-tree (one example of multi-way trees)

---

• The (2,4)-tree
  • Other names for the (2,4)-tree:

    2-4 tree 2-3-4 tree

    ---

  • Properties of the (2,4)-tree:

    Size property: Each node has exactly 4 (internal/external) children nodes: Each internal node has 2-4 (i.e,: 2, 3 or 4) subtrees Each external node has 0 subtrees Depth (height) property: Let E be the set of internal nodes which only have external children nodes (I call these nodes: leaf nodes) All node of E must have the same height (depth) All leaf nodes in a 2,4-tree has the same height !!!

    ---

    ---

  • Example: this tree is not a (2,4)-tree:

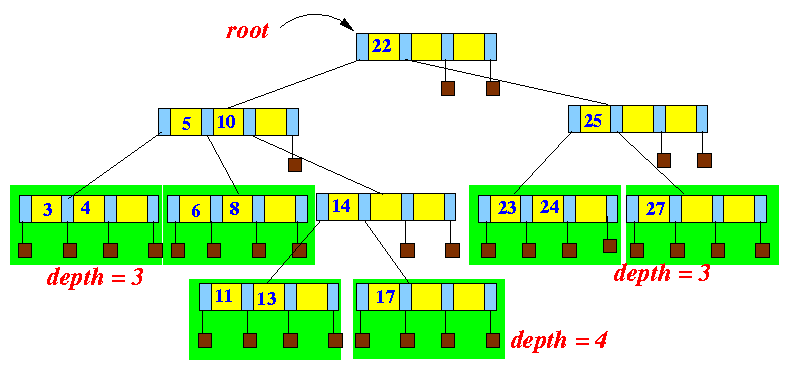
    Because:

    The shaded nodes has no children nodes (i.e., leaf nodes) These nodes have different heights: Some of these nodes have height = 3 Some of these nodes have height = 4

    ---

    ---

  • Example: the following tree is a good (2,4)-tree:

    Because:

    The shaded nodes has no children nodes (i.e., leaf nodes) All these nodes have the same height !!!!!!!!

  ---

  ---

  ---

  ---

• The height of a (2,4)-tree containing n entries
  • Proposition 10.8 (Goodman)

    The height of a (2,4)-tree containing n entries is O(log(n))

    Proof:

    Consider a (2,4)-tree that is maximally populated with entries (i.e., each internal node has 3 keys (4 subtrees) The largest possible number of entries stored in a tree of height h is: # nodes = 1 + 4 + 42 + 43 + ... + 4h-1 4h - 1 = --------- (Mathematica: Sum[ 4^k, {k,0,(h-1)} ]) 3 Max. # keys = 3 * # nodes = 4h - 1 Therefore: n ≤ max. value for n (# keys) ≤ 4h - 1 <==> n+1 ≤ 4h <==> 2log(n+1) ≤ h*log(4) <==> 2log(n+1) ≤ 2*h <==> ½ 2log(n+1) ≤ h ........ 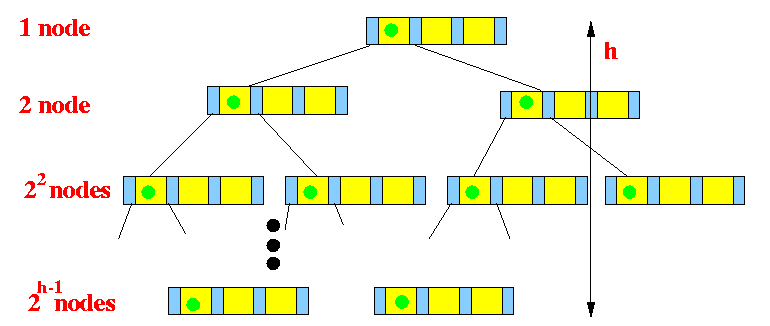(1) Now consider a (2,4)-tree that is minimally populated with entries (i.e., each internal node has 1 keys (2 subtrees) The smallest possible number of entries stored in a tree of height h is: # nodes = 1 + 2 + 22 + 23 + ... + 2h-1 = 2h - 1 (Mathematica: Sum[ 2^k, {k,0,(h-1)} ]) Min. # keys = 1 * # nodes = 2h - 1 Therefore: n ≥ min. value for n (# keys) ≥ 2h - 1 <==> n+1 ≥ 2h <==> 2log(n+1) ≥ h*log(2) <==> 2log(n+1) ≥ h ........ (2) From Equations (1) and (2), we conclude that: 2log(n+1) --------- ≤ h ≤ 2log(n+1) 2 Therefore: h = O(log(n))            Q.E.D.

  ---

  ---

• Worst case running time for search operation in (2,4)-tree
  • The search operation for a (2,4)-tree is bounded by the height of the (2,4)-tree

  • Therefore:

    Worst case runing time of searching in (2,4)-tree = O(log(n))

  ---

  ---

  ---

  ---

• Other multi-way search trees
  • There are many other types of multi-way search trees

    Common property:

    All of them are balanced (I.e., nodes with no children are all of the same height)

    ---

    ---

  • A commonly used type of multiway search tree is the B-tree ("B" is not for "binary", nobody knows, some suspects it stands for "Boeing")

    Rudolf Bayer and Ed McCreight invented the B-tree while working at Boeing Research Labs in 1971 (Bayer & McCreight 1972), but they did not explain what, if anything, the B stands for. Wikipedia: click here