- Deleting an entry e from a
node p with
exactly 1 entry:
- will produce an
"empty" node....
- This condition is called an underflow
- will produce an
"empty" node....
- Comment:
- The exact meaning of
underflow is:
- A node that violates the subtree range condition is in an overflow (too many subtrees) or in an underflow (too few subtrees) condition
- You will see that delete will
also propagate up into
the tree by a
merge operation
- The merge operation
will remove:
- one entry
- one subtree (the child node that got "merged into oblivion" will disappear)
- The resulting node
in a 2,4-tree will
have:
- Zero entries
- But: One subtree
- The merge operation
will remove:
- So technically, the node
is not empty, but
underflow because:
- Number of subtrees of a node
in a 2,4-tree must be
between 2 to 4
- The underflow node has 1 subtree
- Number of subtrees of a node
in a 2,4-tree must be
between 2 to 4
- The exact meaning of
underflow is:
- There are 2 methods used to
handle underflow
(= too few subtrees):
- Transfer
one
subtree from
an immediate sibling node
into the underflow node
- Merge
the underflow node (with has < 2 subtrees)
with one of the
immediate sibling nodes
(After the merge, the resulting node will have enough subtrees)
- Transfer
one
subtree from
an immediate sibling node
into the underflow node
- Brief overview
for handling an underflow situation in
the node p
(i.e., node p has
fewer than
2 subtrees):
- If one (left or right)
immediate sibling node of
node
has ≥ 3 subtrees:
- Transfer a
subtree from
the sibling node into the
underflow node
Because a subtree requires a search key to decide the branch direction, to keep the correct key storage structure, the tree transfer operation requires:
- Transfer the
entry from node p's parent
to replace
the
deleted entry e
in node p,
and
- Transfer an entry from the immediately sibling to node p's parent
- Transfer a
subtree from
the sibling node into the
underflow node
- If
both immediate sibling nodes
of node p
have 1 entry:
- Merge:
- Node p's parent entry
(1 entry)
- Node p's sibling node (with 1 entry in it)
into one single node
- Node p's parent entry
(1 entry)
Notice that:
- The merge operation
will remove:
- One entry from node p's parent node
- One subtree from node p's parent node
Consequently:
- Node p's parent node can itself become underflow (i.e., has 1 subtree) !!!
Solution:
- Repeat
the same procedure
at p's parent node
- In other words:
- Solve the same problem at a node higher up in the tree
- In yet other words:
- Use recursion !!!
- Merge:
- If one (left or right)
immediate sibling node of
node
has ≥ 3 subtrees:
- This brief overview is
probably incomprehensive right now...
That's OK. You can skip it for now.
Come back and read it again after we discuss the techniques in details.
Because the above description contains certain insights that help you understand the details.
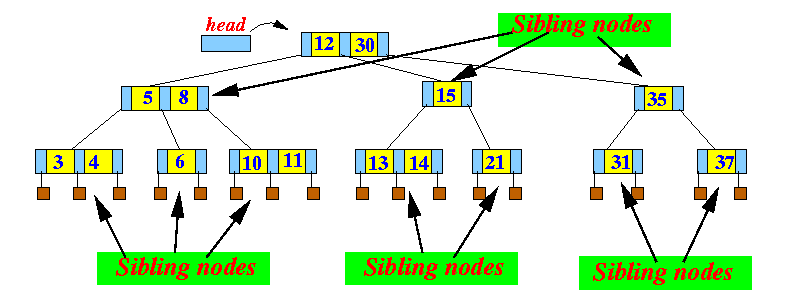
- Terminology:
- Sibling nodes are
nodes that
share the same parent node
Example:
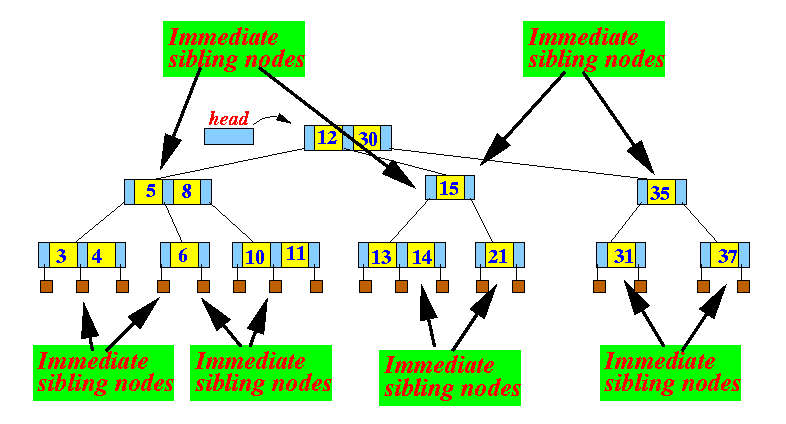
- What I (not in text books)
call immediate sibling nodes, are
sibling nodes that are
next to each other
Example:

- Sibling nodes are
nodes that
share the same parent node
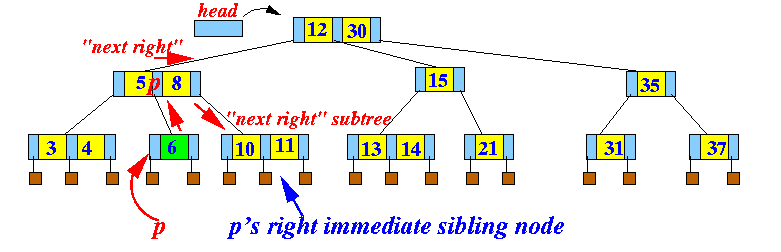
- How to find the
immediate sibling nodes:
- The immediate right sibling
node of a node p is
found at the
root of the
"next right" subtree
of
p's parent node
Example:
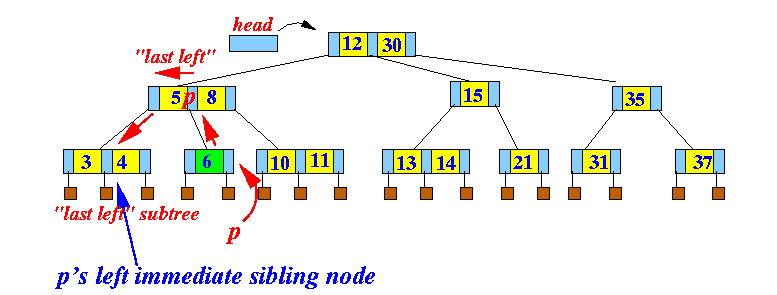
- The immediate left sibling
node of a node p is
found at the
root of the
"last left" subtree
of
p's parent node
Example:
- The immediate right sibling
node of a node p is
found at the
root of the
"next right" subtree
of
p's parent node
- Technique:
- If an underflow condition occurs
in a delete operation, and one of the
immediate sibling nodes
has ≥ 3 subtrees,
we can
solve the
underflow condition
by:
- A subtree transfer
from:
sibling node (with ≥ 3 subtrees) ====> underflow node
- A subtree transfer
from:
- If an underflow condition occurs
in a delete operation, and one of the
immediate sibling nodes
has ≥ 3 subtrees,
we can
solve the
underflow condition
by:
- Transfer with its
right sibling:
- Let's start with a delete operation
that caused an
underflow:
remove(6)
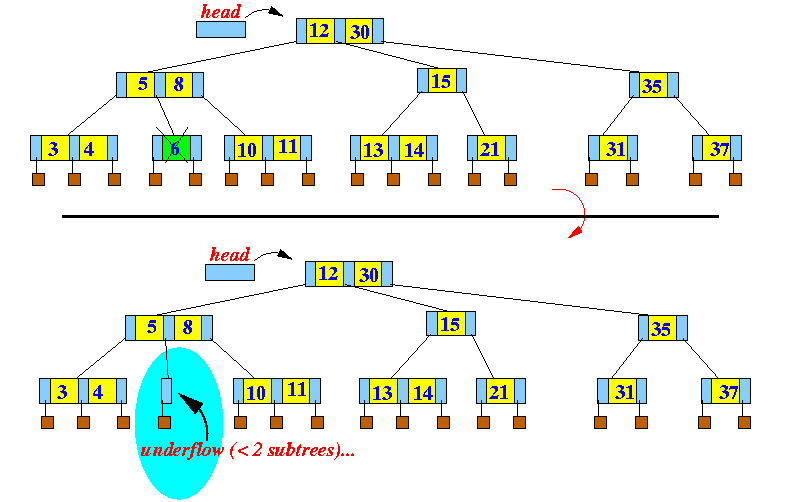
- Transfer a
subtree from the
right sibling:
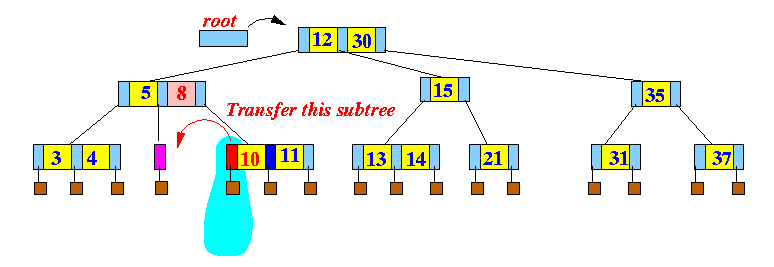
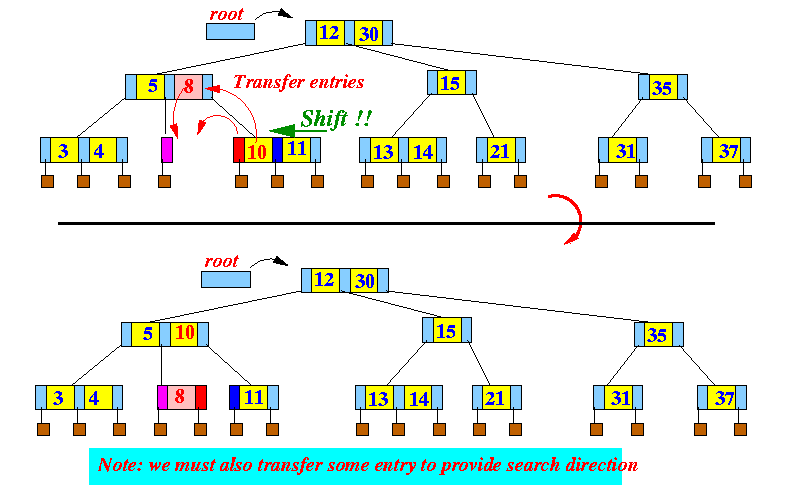
In order to provide the correct search direction for the transfered subtree, we must also transfer so entries (with keys)
Spefically:
- left most entry
in sibling node
⇒ "search key" entry in parent node
⇒ left most entry in underflow node
Graphically:
More complete picture:
- The following example show a
fuller picture ---
in general, there is a subtree
under the red reference:
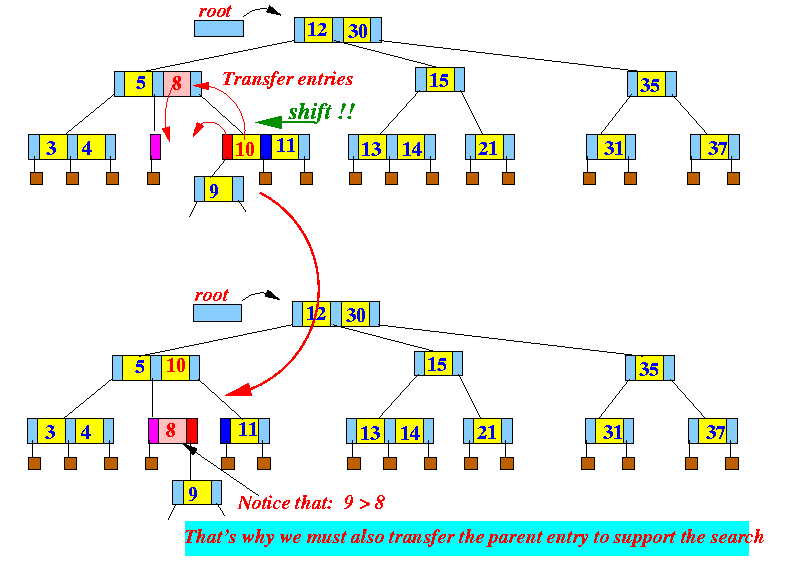
- left most entry
in sibling node
- Let's start with a delete operation
that caused an
underflow:
remove(6)
- Transfer with its
left sibling:
- Delete the
entry:

- Transfer
a subtree
from your left sibling:
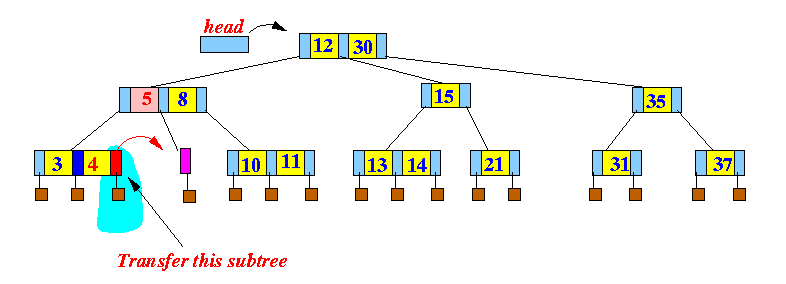
To support the search structure, we must also transfer some entries as follows:

Note:
- Again, we must transfer the
entry from the parent node
into the underflow flow
(along with the transfered subtree) to
keep the search structure
consistent.
- We must also transfer an entry from the left child into the parent node
- Again, we must transfer the
entry from the parent node
into the underflow flow
(along with the transfered subtree) to
keep the search structure
consistent.
- Delete the
entry:
- Very important note:
- When we transfer a subtree
reference into another node,
we must:
- Update the parent reference of the root node in the subtree !!!
- Example:
- We will see later that
the delete operation can
cause cascaded transfers
up the tree.
We may have to perform a transfer where the red reference is a reference to a subtree:
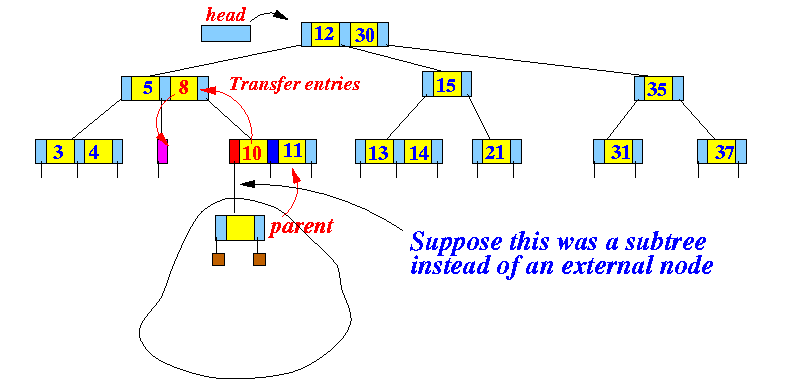
- After the
transfer operation, the
parent node of
the subtree has changed:
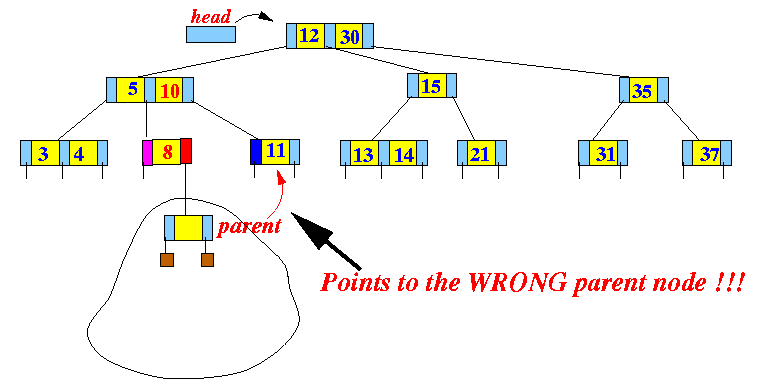
- You must update the
parent reference
of the root node in the
subtree !!!
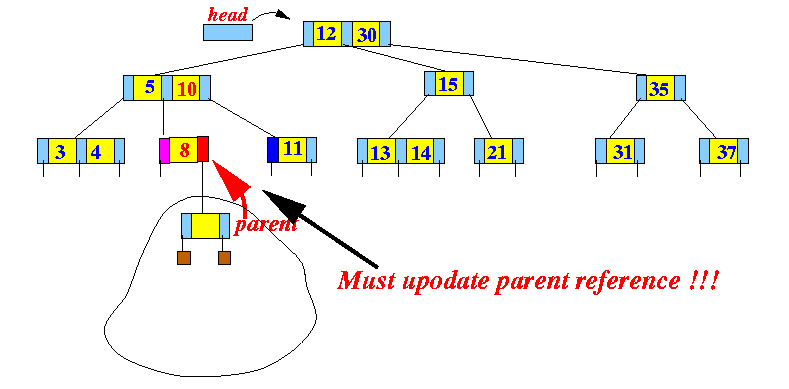
- We will see later that
the delete operation can
cause cascaded transfers
up the tree.
- When we transfer a subtree
reference into another node,
we must: