- The Hungarian Algorithm for
the Transportation Problem is also
a primal-dual Simplex method
- It is a simplex modification of the Hungarian Algorithm for the Assignment Problem
- Recall the Goal:
- Find a minimum cost
"transportation (flow) assignment"
in a weighted bi-partite graph
Example weighted bi-partite graph:
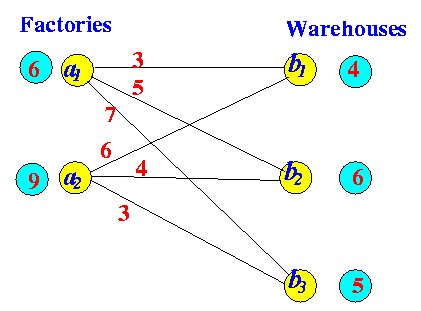
- Find a minimum cost
"transportation (flow) assignment"
in a weighted bi-partite graph
- Pseudo code:
Construct a subgraph graph G consisting of the "best cost edge" Find a maximal flow in subgraph G repeat until all supplies are exhausted { Add the "next best cost edge" to G; // Notice the quotes: it's more complex that just // looking at the cost of an edge Find a maximal flow in (modified) subgraph G; }
- Recall the Transportation Problem
ships products from
factories to
the warehouses
This shipment is equivalent to commidity flow
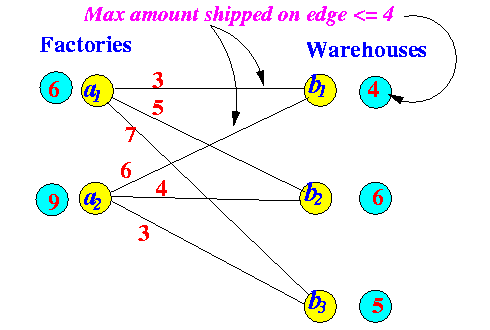
- Capacity of edges in the Transportation problem:
- Capacity of an edge
in the Transportation Problem =
residual capacity of
the warehouse connected to that edge
Example:
- Capacity of an edge
in the Transportation Problem =
residual capacity of
the warehouse connected to that edge
- The shipment of
produce from a factory → warehouse
will:
- Decrease the
amount of supply in the
sending factory
- Decrease the amount of capacity (demand) in the receiving warehouse
Example:
- Initial Transportation Problem:

- Suppose we ship 2 units
from
a1 → b1
Result:

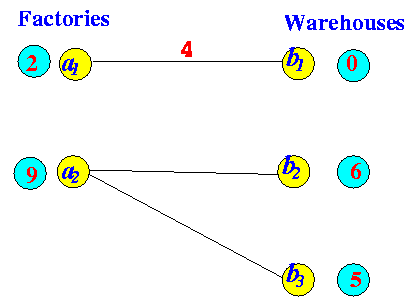
Note:
- When the capacity (demand)
of a warehouse is
reduced, the
capacity of its
attached edges are
also reduced
Example:

- Decrease the
amount of supply in the
sending factory
- Recall: flow augmenting path
- Flow Augmenting Path =
a path from source to sink consisting of
- Forward edges
that is not saturated
- Backward edges with flow > 0
(These are the 2 kinds of "flow augmenting edges in network flow)
- Forward edges
that is not saturated
- Flow Augmenting Path =
a path from source to sink consisting of
- Flow augmenting edges in a Transportation graph:
- Edge from X → Y
(forward edge)
where the capacity (demand) > 0
- Edge from Y → X (backward edge) where flow > 0
(We just apply the definition of the flow augmenting path to the Transportation bi-partite graph:
-
forward edges always run from
X → Y and
backward edges always run from Y → X)
- Edge from X → Y
(forward edge)
where the capacity (demand) > 0
- Example Transportation problem:

Cost Matrix: | b1 b2 b3 ----+------------------ A1 | 3 5 7 A2 | 6 4 3
- The Hungarian algorithm: initial step
- Initial step:
- For each vertex ∈ X:
- find the minimal cost edge
and
- subtract its weight
from
all weights connected with that vertex.
You will get at least one 0-weight edges for each node.
Example:
Min. weight edge of each node ∈ X After subtracting cost from other edges | b1 b2 b3 ----+------------------ A1 | 3 5 7 A2 | 6 4 3| b1 b2 b3 ----+------------------ A1 | 0 2 4 A2 | 3 1 0
- find the minimal cost edge
and
- For each vertex ∈ Y:
- find the minimal cost edge
and
- subtract its weight
from
all weights connected with that vertex.
You may get more 0-weight edges (and you not get any more)
Example:
Min. weight edge of each node ∈ X After subtracting cost from other edges | b1 b2 b3 ----+------------------ A1 | 0 2 4 A2 | 3 1 0| b1 b2 b3 ----+------------------ A1 | 0 1 4 A2 | 3 0 0 - find the minimal cost edge
and
- For each vertex ∈ X:
- Consider the subgraph consisting only of the
0-weight edges
after step 0:
Subgraph Original graph 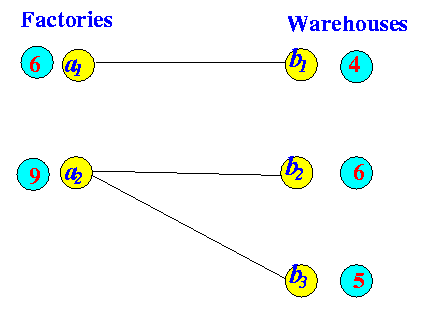

Note:
- Just as in the Assignment Problem, the 0-weight edges will provide the lowest possible cost if we can maximum flow (satisfying all the supplies in set X
- Initial step:
- Finding a maximum flow in
the subgraph of the
Transportation Problem:
- Important:
- We are trying to find a
maximal flow in the
subgraph consisting only of the
0-weight edges
- So we will be using only these edge:

Remember that:
- The capacity in the vertices ∈ Y acts as capacity of the edges
- We are trying to find a
maximal flow in the
subgraph consisting only of the
0-weight edges
- A very simple way to find
flow augmenting paths in
the Transportation subgraph:
- Label
all vertices
xi ∈ X with
supply > 0 with
"*"
(If all vertices ∈ X has supply = 0, the algorithm terminates)
- For every newly labeled vertex
xi
do:
- label all adjacent unlabeled vertices yj ∈ Y with the label "xi"
I.e., we always use the forward edges.
This is because a forward edge can always be part of a flow augmenting path:
- If a forward edge is
unsaturated,
it can carry more flow forward
- If a forward edge is saturated, it can be part of a flow augmenting path by reducing the flow backwards
- For every newly labeled vertex
yj
do:
- label all adjacent unlabeled vertices xi ∈ X with the label "yj" if edge (xi, yj) has flow > 0
Because we will use this edge only as a backward edge and as such, it can only be flow augmenting if flow > 0
- Repeat steps 2 and 3
until:
- Either
a vertex yj
∈ Y
with demand (capacity) > 0
receives a label
- In this case, we have a breaktrough
- Trace starting from vertex xi back to the "*" vertex to find the flow augmenting path
- In this case, we have a breaktrough
- OR:
after the labeling procedure
terminates,
there are no
labeled
vertices xi
with demand > 0
- In this case, we must
add more (next least cost) edges
- We use the same algorithm as in the Assignment Problem to add new edges to the subgraph
- In this case, we must
add more (next least cost) edges
- Either
a vertex yj
∈ Y
with demand (capacity) > 0
receives a label
Example:
Find a Flow Augmenting Path After augmenting flow 
Find a Flow Augmenting Path After augmenting flow 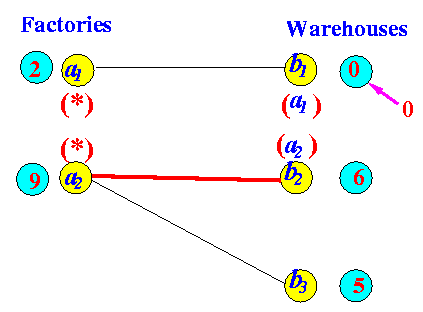
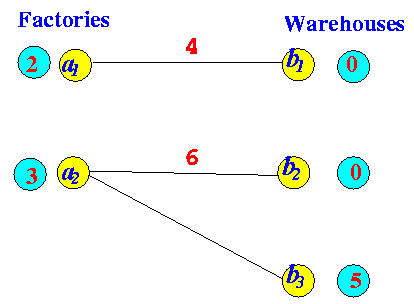
Find a Flow Augmenting Path After augmenting flow 

Find a Flow Augmenting Path No flow augmenting path found 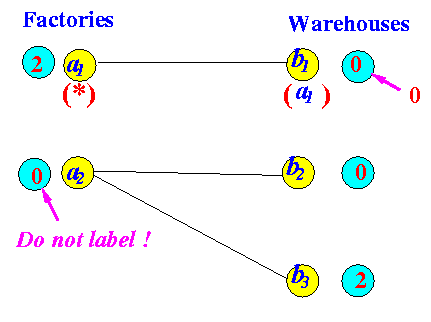
* | b1 b2 b3 ----+------------------ * A1 | 0 1 4 A2 | 3 0 0Note:
- The graph (in table form) includes the labels made by the last step of the max. flow algorithm
- Label
all vertices
xi ∈ X with
supply > 0 with
"*"
- If matching = maximum
(all vertices ∈ X, then we are
done
But in this case, we are not done (yet) and enter the iterative step
Iterative step:
- Add
the "next least cost edge(s)"
to the subgraph
(it's more complex
that just finding the smallest cost,
because you have to consider the effect of
other nodes) and
- Find a new maximal mathcing
- Add
the "next least cost edge(s)"
to the subgraph
(it's more complex
that just finding the smallest cost,
because you have to consider the effect of
other nodes) and
- Important:
- Iterative step:
- Iterative step
(only doen when the matching is not maximum (complete)):
- Add the next least cost edge(s):
- Look
in the full bi-partite graph
(with the label of the
maximum flow algorithm added):
* | b1 b2 b3 ----+------------------ * A1 | 0 1 4 A2 | 3 0 0
- Find
all edges (with cost > 0)
going from a
labeled vertex ∈ X
to an
unlabeled vertex ∈ Y
* | b1 b2 b3 ----+------------------ * A1 | 0 1 4 A2 | 3 0 0Find the minimum cost δ:
- δ = 1
- For each edge
with cost > 0 such that:
labeled vertex ∈ X
→
unlabeled vertex ∈ Y:
- subtract δ from the cost of the edge
For each edge with cost > 0 joining an unlabeled vertex ∈ X → labeled vertex ∈ Y :
- add δ from the cost of the edge
(This addition and subtraction is actually a pivoting operation in the Simplex Algorithm !!)
Example:
Before any operations After the subtract step After the addition step * | b1 b2 b3 ---+--------------- * A1 | 0 1 4 A2 | 3 0 0* | b1 b2 b3 ---+--------------- * A1 | 0 0 3 A2 | 3 0 0* | b1 b2 b3 ---+--------------- * A1 | 0 0 3 A2 | 4 0 0Add the new 0-cost edges to the subgraph:

- Look
in the full bi-partite graph
(with the label of the
maximum flow algorithm added):
- Find a max flow in the
new subgraph
(by labelling)
- There are no supply vertex
with supply > 0
- I.e.: all products
have been transported
- We have found the optimum solution !
Find a Flow Augmenting Path After augmenting flow 
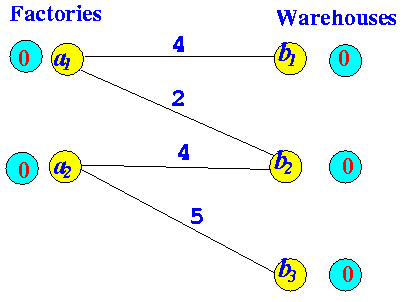
Find a Flow Augmenting Path Optimal !!! 
- There are no supply vertex
with supply > 0
- Add the next least cost edge(s):
- Iterative step
(only doen when the matching is not maximum (complete)):
- Problem description:
Transportation graph Cost Matrix 
| b1 b2 b3 b4 ----+--------------------- a1 | 5 4 7 6 a2 | 2 5 3 2 a3 | 6 3 4 4 - Find the optimum (least cost)
transportation scheme.
- Solution:
- Initialization:
- Subtract the
least cost of
each vertex ∈ X from
all weights connected to that vertex
This is the same as:
- Subtract the smallest value in each row from all other values in that row
Result:
Before subtraction: | b1 b2 b3 b4 ----+--------------------- a1 | 5 4 7 6 a2 | 2 5 3 2 a3 | 6 3 4 4After subtraction: | b1 b2 b3 b4 ----+--------------------- a1 | 1 0 3 2 a2 | 0 3 1 0 a3 | 3 0 1 1
- Subtract the
least cost of
each vertex ∈ Y from
all weights connected to that vertex
This is the same as:
- Subtract the smallest value in each column from all other values in that row
Result:
Before subtraction: | b1 b2 b3 b4 ----+--------------------- a1 | 1 0 3 2 a2 | 0 3 1 0 a3 | 3 0 1 1After subtraction: | b1 b2 b3 b4 ----+--------------------- a1 | 1 0 2 2 a2 | 0 3 0 0 a3 | 3 0 0 1
- Subtract the
least cost of
each vertex ∈ X from
all weights connected to that vertex
- Initial Subgraph:
- Subgraph with 0-weight edges:

- Find a Max flow:
Labelling to find "FAP" After increasing flow 
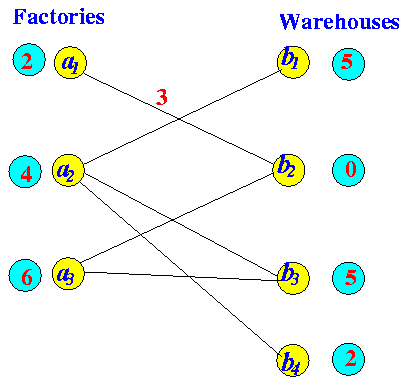
Labelling to find "FAP" After increasing flow 
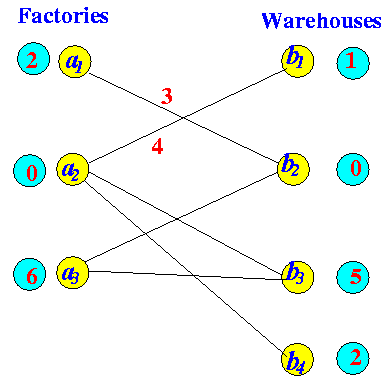
Labelling to find "FAP" After increasing flow 
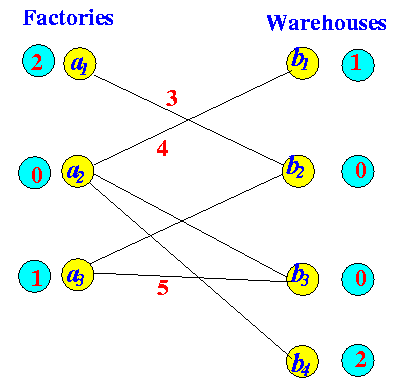
Labelling to find "FAP" Prepare to add more edges... 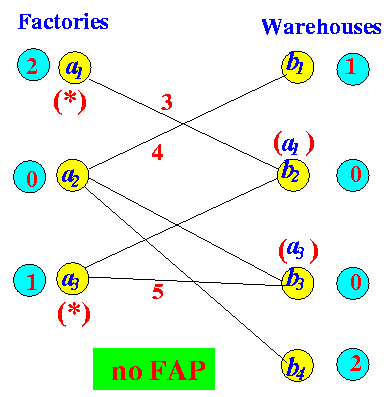
Labeled nodes at end of algorithm: * * | b1 b2 b3 b4 ----+--------------------- * a1 | 1 0 2 2 a2 | 0 3 0 0 * a3 | 3 0 0 1
- Subgraph with 0-weight edges:
- Iteration 1:
- The incomplete solution:

Edges labeled xi → unlabeled yj: (marked red) * * | b1 b2 b3 b4 ----+--------------------- * a1 | 1 0 2 2 a2 | 0 3 0 0 * a3 | 3 0 0 1 δ = 1
- Recalculate edge costs to find new 0-weight edges:
Subtract δ (1) from the cost of edges labeled xi → unlabeled yj:
Result: * * | b1 b2 b3 b4 ----+--------------------- * a1 | 0 0 2 1 a2 | 0 3 0 0 * a3 | 2 0 0 0Add δ (1) to the cost of edges unlabeled xi → labeled vertex yj (only when cost of edge > 0)
Result: * * | b1 b2 b3 b4 ----+--------------------- * a1 | 0 0 2 1 a2 | 0 4 0 0 * a3 | 2 0 0 0
- New subgraph with
additional
0-weight edges:

- Find a Maximal Flow (through labelling):
Labelling to find "FAP" After increasing flow 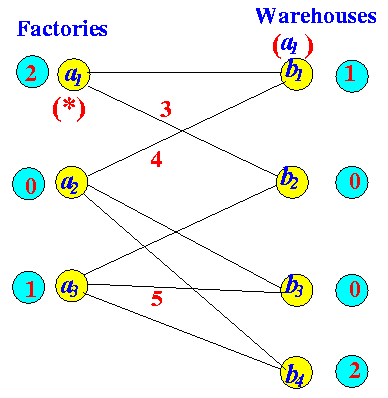
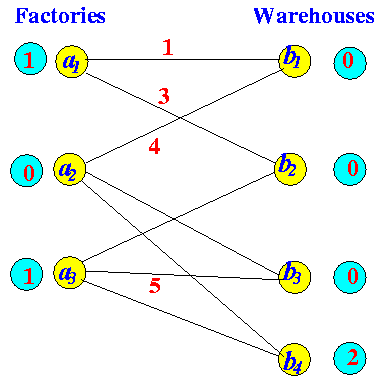
Labelling to find "FAP" After increasing flow 
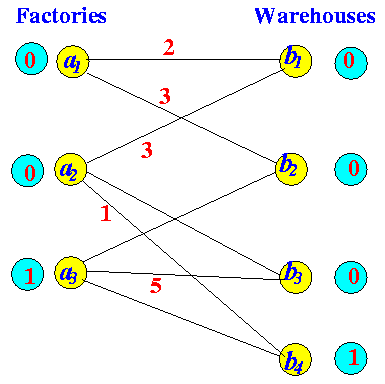
Labelling to find "FAP" After increasing flow 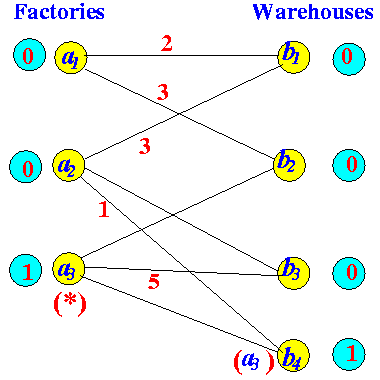

- The incomplete solution:
- No more
unsatisfied supplies
in X
We have found the optimal solution:
Transportation graph with edge cost Min cost flow solution 

Cost of optimum solution:
Cost = 2*5 + 3*4 + 3*2 + 1*2 + 5*4 + 1*4 = 10 + 12 + 6 + 2 + 20 + 4 = 54
- Initialization:
- Compare to the solution obtained by LP:
Value of objective function: 54.00 Actual values of the variables: x11 2 x12 3 x13 0 x14 0 x21 3 x22 0 x23 0 x24 1 x31 0 x32 0 x33 5 x34 1
Side by side comparison:
LP solution Solution by Hungarian Algorithm 

Note:
- The cost of both solutions are the same (= 54) !!!