- The Simplex method uses (invariant) row operations on matrices in Linear Algebra to find the optimal solution of an LP
|
|
- Consider the following system of equations:
2 x1 + 4 x2 = 16 3 x1 + 2 x2 = 12
- The equality (=)
means that the values in the
left hand side and right hand side
of "=" are in "balance".
- The systems of equations above can be represented
by this figure:
2 x1 + 4 x2 = 16 3 x1 + 2 x2 = 12

- Invariant row operation 1:
- You can multiply (or divide) both sides of an equation by the same factor, and the resulting equality will hold (= true).
Example: divide the first equation by 2 (= multiply first equation by 0.5)
2 x1 + 4 x2 = 16 (equation 1) 3 x1 + 2 x2 = 12 (equation 2) Manipulation: 0.5 × (2 x1 + 4 x2) = 0.5 × (16) ==> x1 + 2 x2 = 8 Result: x1 + x2 = 8 (equation 1) 3 x1 + 2 x2 = 12 (equation 2)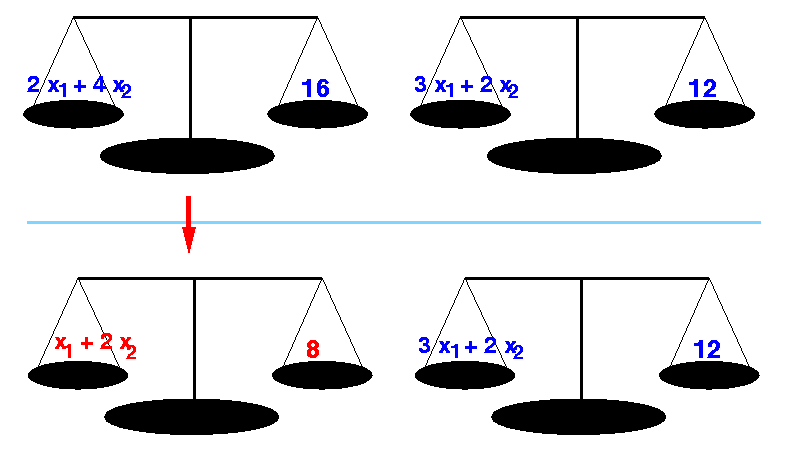
- Invariant row operation2:
- You can add (or subtract) a multiple of one equation (row) to another equation (row) and the resulting equality will hold (= true)
Example: subtract 3 × the first equation from the second equation
x1 + 2 x2 = 8 (row 1) 3 x1 + 2 x2 = 12 (row 2) (row 2) ===> 3 x1 + 2 x2 = 12 3 x (row 1) ===> 3 x1 + 6 x2 = 24 - (subtract) ------------------------------- 0 x1 - 4 x2 = -12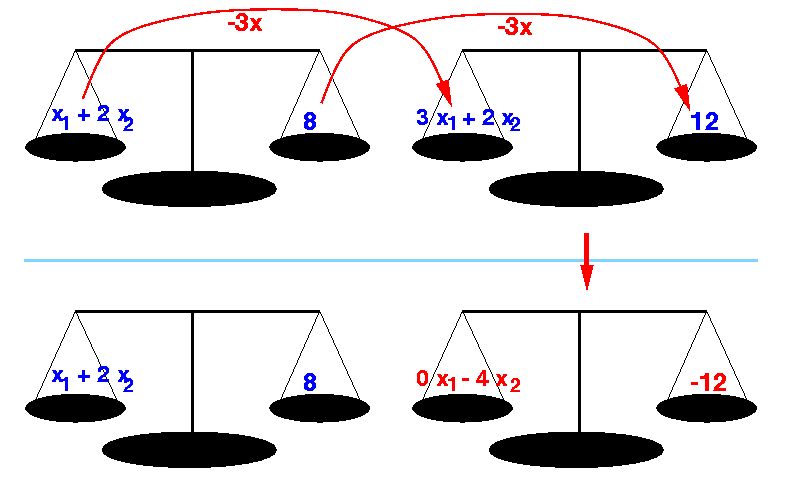
- Pivot operating:
(a.k.a.: pivoting)
- Pivot operation =
to apply invariant row operations
to Simplex Tableau
such that:
- A non-basic variable
will become a
basic variable
and
- A (some other) basic variable will become a non-basic variable
- A non-basic variable
will become a
basic variable
and
- In other words:
- A pivot operation will change the basic solution !!!
Note:
- Before we
perform the
pivot operation,
we will make sure that the
objective function
will
increase when we
perform the
pivot operation !!!
We will learn how to select a pivot later....
- Pivot operation =
to apply invariant row operations
to Simplex Tableau
such that:
- Pivot or
pivot element
- Pivot =
an element in the
Simplex Tableau
that forms the
central element
in the
pivot operation
The pivot operation is apply using the pivot element as its parameter
- Pivot =
an element in the
Simplex Tableau
that forms the
central element
in the
pivot operation
- The steps of
the pivot operation:
- Divide the
row
containing the
pivot element by the
value of the pivot
- This step will make the pivot element = 1
- Use row operations
to make the
other elements of the
column vector
containg the
pivot equal to
0
- This step will make the column vector containg the pivot equal to a canonical unit vector !!
- Divide the
row
containing the
pivot element by the
value of the pivot
- Example:
perform a
pivot operation
using the pivot element "3"
- The starting
basic solution:
x1 x2 s1 s2 z | RHS ==========================+==== -1 -1 0 0 1 | 0 1 2 1 0 0 | 8 3 2 0 1 0 | 12 ^ | Use this as pivot element (The pivot operation will transform this column into a canonical unit vector with the pivot element becoming 1) Note: Current basic variables: s1 s2 z
- We will now:
- Perform a pivot operation
using the element
3 as
pivot
(I.e., these sequence of operation are performed in respect to that element)
- Perform a pivot operation
using the element
3 as
pivot
- Pivot procedure:
x1 x2 s1 s2 z | RHS ==========================+==== -1 -1 0 0 1 | 0 1 2 1 0 0 | 8 3 2 0 1 0 | 12 Step 1: divide the pivot row by the pivot value (= 3)
Result: x1 x2 s1 s2 z | RHS ==========================+==== -1 -1 0 0 1 | 0 (Row 1) 1 2 1 0 0 | 8 (Row 2) 1 ⅔ 0 ⅓ 0 | 4 (Row 3) Step 2: Use row operations to make the other value under x1 equal to 0 (I.e.: Add a multiple of row 3 to the other rows)
x1 x2 s1 s2 z | RHS ==========================+==== -1 -1 0 0 1 | 0 (Row 1) 1 2 1 0 0 | 8 (Row 2) 1 ⅔ 0 ⅓ 0 | 4 (Row 3) Row operation: row 1 = row 1 + (1) × (row 3) Result: x1 x2 s1 s2 z | RHS ==========================+==== 0 -⅓ 0 ⅓ 1 | 4 (Row 1) 1 2 1 0 0 | 8 (Row 2) 1 ⅔ 0 ⅓ 0 | 4 (Row 3) Row operation: row 2 = row 2 - (1) × (row 3) Result: x1 x2 s1 s2 z | RHS ==========================+==== 0 -⅓ 0 ⅓ 1 | 4 (Row 1) 0 1⅓ 1 -⅓ 0 | 4 (Row 2) 1 ⅔ 0 ⅓ 0 | 4 (Row 3) ^ | New basic variable !!
- The new Simplex Tableau:
x1 x2 s1 s2 z | RHS ==========================+==== 0 -⅓ 0 ⅓ 1 | 4 (Row 1) 0 1⅓ 1 -⅓ 0 | 4 (Row 2) 1 ⅔ 0 ⅓ 0 | 4 (Row 3)
- The starting
basic solution:
- The new set of basic variables:
- x1
- s1
- z
The basic solution corresponding to the new Simplex Tableau is:
- x2 = 0 (non-basic variable)
- s2 = 0
(non-basic variable)
- x1 = 4 (basic variable, RHS)
- s1 = 4 (basic variable, RHS)
- z = 4 (basic variable, RHS)
- Graphical depiction of this
basic solution:
(x1 = 4, x2 = 0)
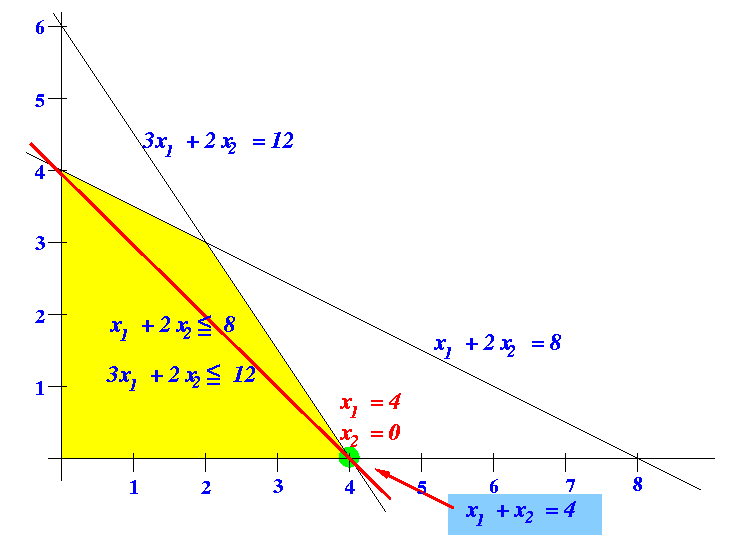
Note:
- The basic solution is
again a
"corner" point in the
feasible region
- This basic solution is
better than the
previous one because:
- The objective value
z = 4
(The previous solution has an objective value z = 0)
- The objective value
z = 4
- The basic solution is
again a
"corner" point in the
feasible region
- The Simplex Algorithm:
T = an initial Simplex Tableau; // How: // Add surplus variables // to obtain a basic solution Find a pivot element p in T that // Discussed next makes the obj. function increase in value; while ( p can be found ) { T = Perform pivot operation on p in T // Discussed above Find a pivot element p in T that makes the obj. function increase in value; }
- Mathematics behind the selection of the pivot:
- I will omit the
Mathematical theory
behind the
how to
select the pivot
(Requires matrix manipulations)
- I will only show you
rules on how to
pick the pivot
The pivot selection rules are based on 2 Mathematical results:
- The pivot column is selected
by an optimality criterium
- The pivot row is selected by a feasibility criterium
- The pivot column is selected
by an optimality criterium
- I will omit the
Mathematical theory
behind the
how to
select the pivot
- Pivot row and
pivot column:
- A pivot element is uniquely
identified by
- a pivot row
- a pivot column
Example:

- A pivot element is uniquely
identified by
- Terminology:
objective row (and
constraint rows)
- These terms will help understand the descriptions of the algorithm:

Explanation:
- The first row of the
Simplex tableau is called the
objective row
- (Because it is obtained from the objective function z = x1 + x2 or: z - x1 - x2 = 0 )
- The other rows of the Simplex tableau is called the constraint rows
- The first row of the
Simplex tableau is called the
objective row
- These terms will help understand the descriptions of the algorithm:
- Determining the
pivot column:
- The pivot column
= the
column of the
largest negative cofficient
in the
objective (first)
row
in the
Simplex Tableau
(Break ties aribitrarily)
Reason:
- The largest negative value will make the objective function increase the fastest in value when we change the value in that column.
Example:

- The pivot column
= the
column of the
largest negative cofficient
in the
objective (first)
row
in the
Simplex Tableau
- Terminology:
test ratio
- Test ratio of
a constraint row is defined as
follows:
-
If coefficient in the pivot column > 0:
RHS test ration of a constraint row = ---------------------------------- coefficient in the pivot columnelse:
test ration of a constraint row = undefined
Example:

The test ratios of the 2 constraint rows are:
test ratio(constraint 1) = 8/1 = 8 test ratio(constraint 2) = 12/3 = 4
-
If coefficient in the pivot column > 0:
Note:
- The test ratio of the constraint row k represents an upper bound on the amount that the variable in the pivot couln can increase before the corresponding constraint k will be violated
- Test ratio of
a constraint row is defined as
follows:
- Determining the
pivot row:
- The pivot row =
the row that contains
the smallest (valid) test ratio
(I.e., the coefficient must be > 0)
Example:

Explanation:
- The test ratio of
constraint row 2
has the
smallest value
- Therefore:
- Pivot row = constraint row 2
- The pivot row =
the row that contains
the smallest (valid) test ratio
- The pivot element:
- The pivot element = the element found in the pivot row and pivot column
I I I I
- Linear Program:
max: z = x1 + x2 s.t.: x1 + 2x2 ≤ 8 3x1 + 2x2 ≤ 12 x1 ≥ 0, x2 ≥ 0
- Step 1: transform to system of
linear equation with a basis
Add surplus variables: z - x1 - x2 = 0 x1 + 2x2 + s1 = 8 3x1 + 2x2 + s2 = 12
Lined up: -x1 - x2 + z = 0 x1 + 2x2 + s1 = 8 3x1 + 2x2 + s2 = 12
In Tableau form: x1 x2 s1 s2 z | RHS ==========================+==== -1 -1 0 0 1 | 0 1 2 1 0 0 | 8 3 2 0 1 0 | 12 Basis: s1 s2 zThis is the initial Simplex Tableau
- Pivot step 1:
- Select the
pivot column
using the largest negative coefficient
in the first (objective) row:
Pivot column (break ties arbitrarily) | V x1 x2 s1 s2 z | RHS ==========================+==== -1 -1 0 0 1 | 0 largest negative value 1 2 1 0 0 | 8 3 2 0 1 0 | 12
- Select the
pivot row
using the smallest test ratio
associated to
a positive coefficient:
x1 x2 s1 s2 z | RHS ==========================+==== -1 -1 0 0 1 | 0 (neg. coef - skip it) 1 2 1 0 0 | 8 test ratio = 8/1 = 8 3 2 0 1 0 | 12 test ratio = 12/3 = 4
- Pivot:
Step 1: divide pivot row by pivot element x1 x2 s1 s2 z | RHS ==========================+==== -1 -1 0 0 1 | 0 1 2 1 0 0 | 8 3 2 0 1 0 | 12 | divide row by 3 V x1 x2 s1 s2 z | RHS ==========================+==== -1 -1 0 0 1 | 0 1 2 1 0 0 | 8 1 0.7 0 0.3 0 | 4
Step 2: sweep the pivot column x1 x2 s1 s2 z | RHS ==========================+==== -1 -1 0 0 1 | 0 (Row 1) 1 2 1 0 0 | 8 (Row 2) 1 0.7 0 0.3 0 | 4 (Row 3) After: row 1 = row 1 + 1 × (row 3) x1 x2 s1 s2 z | RHS ==========================+==== 0 -0.3 0 0.3 1 | 4 (Row 1) 1 2 1 0 0 | 8 (Row 2) 1 0.7 0 0.3 0 | 4 (Row 3) After: row 2 = row 2 - 1 × (row 3) x1 x2 s1 s2 z | RHS ==========================+==== 0 -0.3 0 0.3 1 | 4 (Row 1) 0 1.3 1 -0.3 0 | 4 (Row 2) 1 0.7 0 0.3 0 | 4 (Row 3)
- Select the
pivot column
using the largest negative coefficient
in the first (objective) row:
- Corresponding basic solution:
- x1 = 4
- x2 = 0
- Objective value: z = 4
Graphically:

- Pivot step 2:
- Select the
pivot column
using the largest negative coefficient
in the first (objective) row:
Pivot column | V x1 x2 s1 s2 z | RHS ==========================+==== 0 -0.3 0 0.3 1 | 4 (Row 1) 0 1.3 1 -0.3 0 | 4 (Row 2) 1 0.7 0 0.3 0 | 4 (Row 3)
- Select the
pivot row
using the smallest test ratio
associated to
a positive coefficient:
x1 x2 s1 s2 z | RHS ==========================+==== 0 -0.3 0 0.3 1 | 4 0 1.3 1 -0.3 0 | 4 test ratio = 4/1.3 = 3 1 0.7 0 0.3 0 | 4 test ratio = 4/0.7 = 6
- Pivot:
Step 1: pivot row by pivot element x1 x2 s1 s2 z | RHS ==========================+==== 0 -0.3 0 0.3 1 | 4 0 1.3 1 -0.3 0 | 4 divide row by 1.333333 1 0.7 0 0.3 0 | 4 | V x1 x2 s1 s2 z | RHS ==========================+==== 0 -0.3 0 0.3 1 | 4 0 1 0.75 -0.25 0 | 3 1 0.7 0 0.3 0 | 4
Step 2: sweep the pivot column x1 x2 s1 s2 z | RHS ==========================+==== 0 -0.3 0 0.3 1 | 4 (row 1) 0 1 0.75 -0.25 0 | 3 (row 2) 1 0.7 0 0.3 0 | 4 (row 3) After: row 1 = row 1 + 0.333333 × (row 2) x1 x2 s1 s2 z | RHS ==========================+==== 0 0 0.25 0.25 1 | 5 (row 1) 0 1 0.75 -0.25 0 | 3 (row 2) 1 0.7 0 0.3 0 | 4 (row 3) After: row 3 = row 3 - 0.6666666 (0.7) × (row 2) x1 x2 s1 s2 z | RHS ==========================+==== 0 0 0.25 0.25 1 | 5 (row 1) 0 1 0.75 -0.25 0 | 3 (row 2) 1 0 -0.5 0.5 0 | 2 (row 3)
- Select the
pivot column
using the largest negative coefficient
in the first (objective) row:
- Corresponding basic solution:
- x1 = 2
- x2 = 3
- Objective value: z = 5
Graphically:
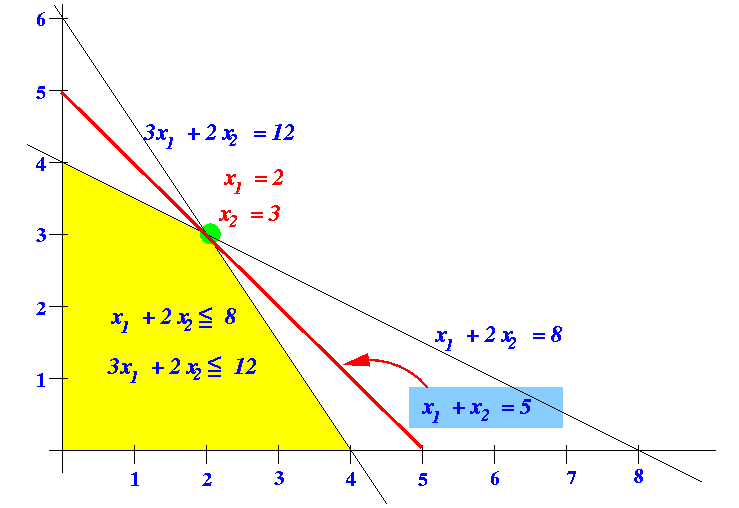
- Pivot step 3:
- Select the
pivot column
using the largest negative coefficient
in the first (objective) row:
x1 x2 s1 s2 z | RHS ==========================+==== 0 0 0.25 0.25 1 | 5 (row 1) - no negative coefficient 0 1 0.75 -0.25 0 | 3 (row 2) 1 0 -0.5 0.5 0 | 2 (row 3)
DONE !!!
(Optimal solution found)
- Select the
pivot column
using the largest negative coefficient
in the first (objective) row: