---

Introduction to Linear constrained optimalization

---

• Linear constrained optimalization
  • Recall: The general form of a constrained opimization problem:

    max f( x1, x2, ..., xn ); // Objective function subject to: g1( x1, x2, ..., xn ) = c1 // Equality constraints g2( x1, x2, ..., xn ) = c2 ... gu( x1, x2, ..., xn ) = cu h1( x1, x2, ..., xn ) ≤ d1 // Inequality constraints h2( x1, x2, ..., xn ) ≤ d2 ... hv( x1, x2, ..., xn ) ≤ dv

    ---

  • Linear constrained optimization:

    Linear constrained optimization = a constrained optimization problem where: the objective function and the constraint functions are: linear functions of x1, x2, ..., xn

    ---

    ---

  • In other words, a linear constrained optimization problem looks like this:

    max a1x1 + a2x2 + ... + anxn ; // Objective function subject to: c11x1 + c12x2 + ... + c1nxn ≤ d1 // Constraints c21x1 + c22x2 + ... + c2nxn ≤ d2 .... cm1x1 + cm2x2 + ... + cmnxn ≤ dm x1 ≥ 0, x2 ≥ 0, ..., xn ≥ 0

  • Note:

    We do not need to use any "="-constraints !!! Because: An "="-constraint can be re-written as two "≤"-constaints: ck1x1 + ck2x2 + ... + cknxn = dk is the same as: ck1x1 + ck2x2 + ... + cknxn ≤ dk ck1x1 + ck2x2 + ... + cknxn ≥ dk Or using only "≤"-constraints: ck1x1 + ck2x2 + ... + cknxn ≤ dk -ck1x1 - ck2x2 - ... - cknxn ≤ -dk There is a trick to transform a linear constrained optimization problem into a form where: x1 ≥ 0 x2 ≥ 0 ... xn ≥ 0 We will learn this trick later....

  ---

  ---

  ---

  ---

• Definitions
  • Linear program

    Linear program = a linear constrained optimization problem

    ---

  • Linear programming

    Linear programming = an algorithm to solve linear programs

  ---

  ---

  ---

  ---

  I I I I

  ---

  ---

• A simple Linear Program (LP)
  • Here is what a linear constrained optimalization problem or Linear Program (LP) looks like:

    max: x1 + x2 s.t.: x1 + 2x2 ≤ 8 3x1 + 2x2 ≤ 12 x1 ≥ 0, x2 ≥ 0

    ---

    ---

  • Note:

    The constraint: xi  ≥  0,    for every i     is assumed in linear programming

    So an LP is usually written as follows:

    max: x1 + x2 s.t.: x1 + 2x2 ≤ 8 3x1 + 2x2 ≤ 12

    The constraints x₁ ≥ 0, x₂ ≥ 0 are implicitly assumed !!!

  ---

  ---

  ---

  ---

  ---

  ---

• Definitions:   "feasible solution" and "feasible region"
  • Given the following LP:

    max: x1 + x2 s.t.: x1 + 2x2 ≤ 8 3x1 + 2x2 ≤ 12

    ---

  • Feasible solution:

    A solution is feasible if it satisfies all constraints So feasibility is only determined by the constraints The objective function has nothing to do with feasibility !!! Example: (x1=1, x2=0) (or (1,0) for brevity) is feasible because: x1 + 2x2 = 1 + 2(0) = 1 ≤ 8 3x1 + 2x2 = 3(1) + 2(0) = 3 ≤ 12 All constraints of the LP are satisfied

    ---

  • Feasible region:

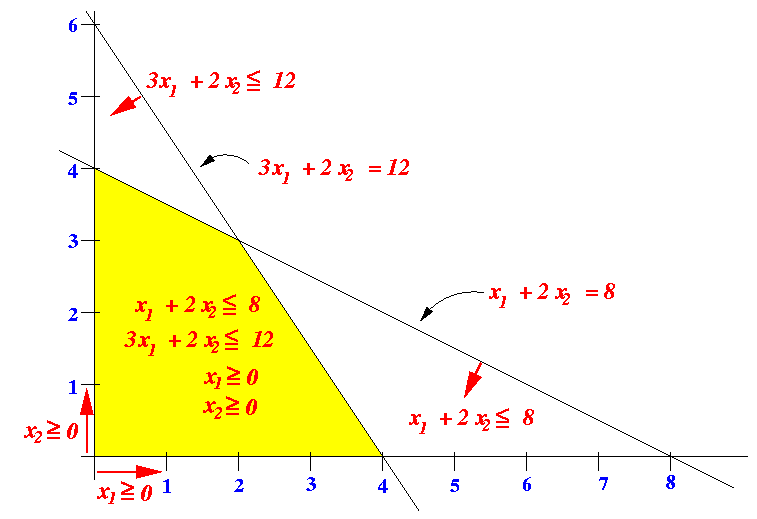
    The feasible region = all feasible solution Note: So feasible region is only determined by the constraints !!! Fact: The feasible region of an LP is always a convex polyhedron No proof, just an external reference (Wikipedia page): click here Example: max: x1 + x2 s.t.: x1 + 2x2 ≤ 8 // Constraints define 3x1 + 2x2 ≤ 12 // the feasible region ! The feasible region of this LP is: The points inside the yellow colored region satisfies all the constraints: x1 + 2x2 ≤ 8 3x1 + 2x2 ≤ 12 x1 ≥ 0 x2 ≥ 0 (Remember that: x1 ≥ 0, x2 ≥ 0 are assumed !!!)

    ---

    ---

  • Constrained optimalization:

    Find the point (a feasible point) inside the feasible region that results in the maximum value for the objective function

  ---

  ---

  ---

  ---

  ---

  ---

• Graphical solution to an LP
  • Suppose we have the following objective function:

    Obj = x1 + x2

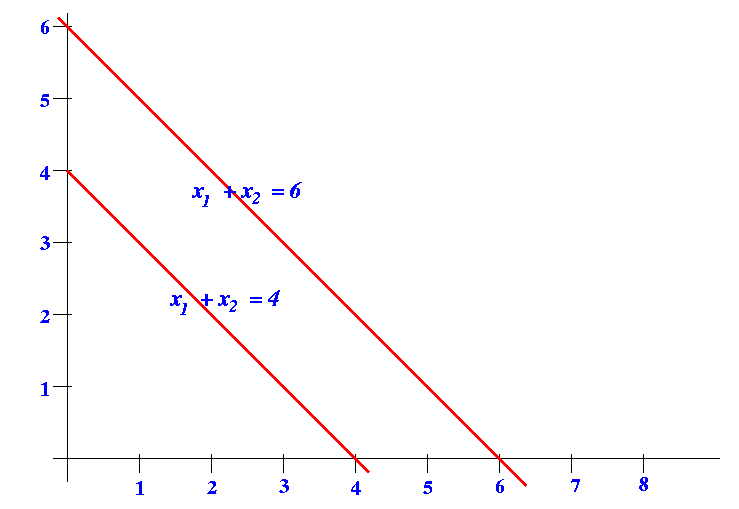
  • Some graphs (plots) depicting the fact that

    x1 + x2 = "some constant value"

    look like this:

    ---

  • How to solve this constrained optimization problem using graphs:

    max: x1 + x2 s.t.: x1 + 2x2 ≤ 8 3x1 + 2x2 ≤ 12

    Answer:

    Because we want to maximize the objective function "x1 + x2": We must find the graph for "x1 + x2 = largest constant" that lies inside the feasible region

    Graphically:

    We can see that:

    The optimal solution is:   x1 = 2,   x2 = 3 The maximum objective value achieved: (x1 + x2) = 5

    Important note:

    The optimal solution to an LP is always a "corner" point on the edge of the polyhedron that makes up the feasible region (No proof... I can point you to some good books on the Simplex Method if you are interested)