- Encoding:
- Encoding = to represent facts with numbers (or patterns)
- Example:
- Sex:
- 0 = male
- 1 = female
- Sex:
- ASCII code: (for the
English alphabet)

- Unicode: (for all languages)
- Unicode
provides a unique number
for every character,
no matter what the platform,
no matter what the program,
no matter what the language.
Reference: click here
- Unicode
provides a unique number
for every character,
no matter what the platform,
no matter what the program,
no matter what the language.
- Common characteristic:
- ASCII and
Unicode are
fixed length codes:
- ASCII code: 8 bits
- Unicode: 16 bits
- ASCII and
Unicode are
fixed length codes:
- Fixed length code:
- Each code has
the same number of bits
- Advantage: easy to encode and decode
- Disadvantage: inefficient (uses more bits)
- Each code has
the same number of bits
- Variable length code:
- Different code can have
a different number of bits
- Advantage: more efficient (uses less bits)
- Disadvantage: harder to encode and decode
I guess the "law of conservation of misery" applies here too....
- Different code can have
a different number of bits
- Morse code:

Note:
- The Morse code uses
2 symbols:
a dot and a dash
- Dot = a short beep
- Dash = a
long beep
- We can represent dot with
0 and
dash with 1 and
get a binary representation
- Notice that:
- Frequently used letters (in English) has shorter codes !!!
This minimizes the number of key strokes of the operator !!
- The Morse code uses
2 symbols:
a dot and a dash
- Fact:
- Different characters appear with different frequencies in a text
Example:
- In English, the
letter e appears
with the highest frequency
in text documents
- Letters x and q are rarely used !!!
- How to improve
efficient
(i.e., use fewer bits
to encode a text document)
- Assign frequent characters a
shorter code word
- Assign infrequent characters a longer code word
- Assign frequent characters a
shorter code word
- Example variable length code:
Character | (Variable length) code -------------+-------------------------- S | 1 E | 01 Y | 10 O | 11 N | 100 ... | ... (code for other letters omitted)Question:
- What text is
encoded by the following
code:
10011
Answer:
10011 = 10 01 1 = Y E S 10011 = 100 11 = N O - What text is
encoded by the following
code:
- Prefix property:
- An encoding
has the prefix property if:
- There is no valid code word in the encoding that is a prefix of another valid code word
- An encoding
has the prefix property if:
- Prefix code
- Prefix code = an encoding that has the prefix property
- Example:
- This encoding is
not
a prefix code:
Character | (Variable length) code -------------+-------------------------- S | 1 E | 01 Y | 10 O | 11 N | 100 ... | ... (code for other letters omitted)because:
1 is valid code word: 1 = (S) Now: 1 is a prefix of 10 (Y) 1 is a prefix of 11 (O) 1 is a prefix of 100 (N)(many violations :))
- This encoding is
not
a prefix code:
- Example:
- This encoding
is
a prefix code:
Character | (Variable length) code -------------+-------------------------- S | 1 E | 01 Y | 001 O | 0001 N | 00001 ... | ... (code for other letters omitted)because:
1 is a valid code word ==> 1 is not a prefix of any other code word 01 is a valid code word ==> 01 is not a prefix of any other code word 001 is a valid code word ==> 001 is not a prefix of any other code word and so on....
- This encoding
is
a prefix code:
- Fact:
- Variable length code must have the prefix property to be avoid ambiguity
- Overview:
- Huffman Coding
is a greedy algorithm
to
find a (good)
variable-length encoding
using the
character frequencies
- The algorithm will:
- Use a minumum length code
to encode the
most frequent character
- Use a 2nd shortest
length code
to encode the
2nd most frequent character
- And so on...
- Use a minumum length code
to encode the
most frequent character
- In order to achive this, the
Huffman coding algorithm
contruct a
binary tree
based on the
frequencies of
each character:
- The characters near the
root of the tree
have the highest frequencies
- The characters located deeper down in the tree have the highest frequencies
- The characters near the
root of the tree
have the highest frequencies
- Huffman Coding
is a greedy algorithm
to
find a (good)
variable-length encoding
using the
character frequencies
- Example: encode the text
abracadabra
- Using ASCII code:
a b r a c a 01100001 01100010 01110010 01100001 01100011 01100001 d a b r a 01100100 01100001 01100010 01110010 01100001
- Huffman encoding:
- Find the frequency of each character
abracadabra a:5 b:2 c:1 d:1 r:2
- For each character,
form a binary tree that consists of
one singleton node:

(I ordered the tree by their frequencies because I will need that in the next step)
- Find the 2 trees with the
lowest frequencies
(break ties arbitrarily) and form
new tree with
a root node equal to the
sum of their
frequencies:
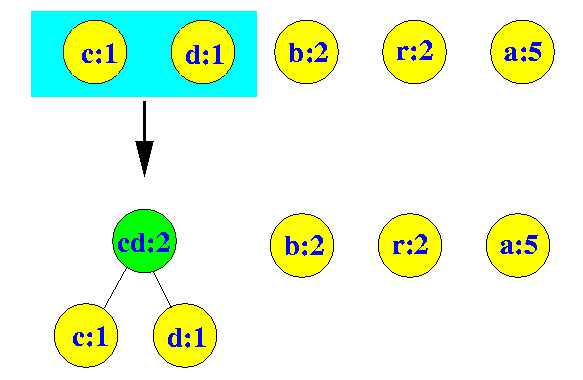
(Now we have 4 binary trees !!!)
- Find the 2 trees with the
lowest frequencies
(break ties arbitrarily) and form
new tree with
a root node equal to the
sum of their
frequencies:

(Now we have 3 binary trees !!!)
- Find the 2 trees with the
lowest frequencies
(break ties arbitrarily) and form
new tree with
a root node equal to the
sum of their
frequencies:
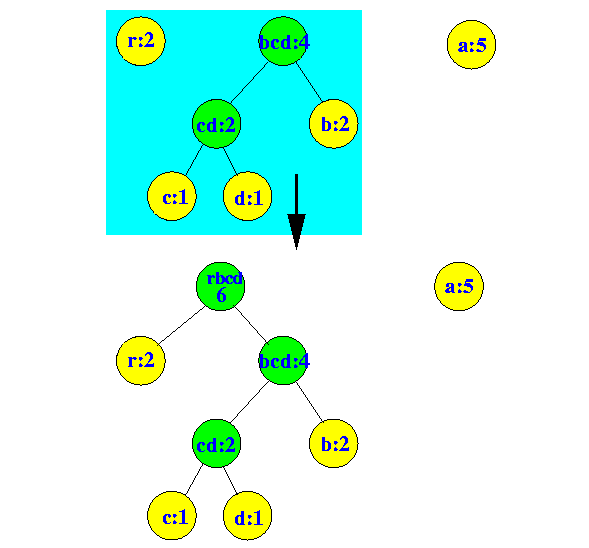
(Now there are 2 binary trees !!!)
- Find the 2 trees with the
lowest frequencies
(break ties arbitrarily) and form
new tree with
a root node equal to the
sum of their
frequencies:

(Now there is only 1 binary tree, and we are done !!!)
- Assign the Huffman code
as follows:
- When you take a left branch, append a 0 to the code word
- When you take a right branch,
append
a 1 to the code word
- The path from the root to a leaf node (that store the characters) is the code word for that character
Example:
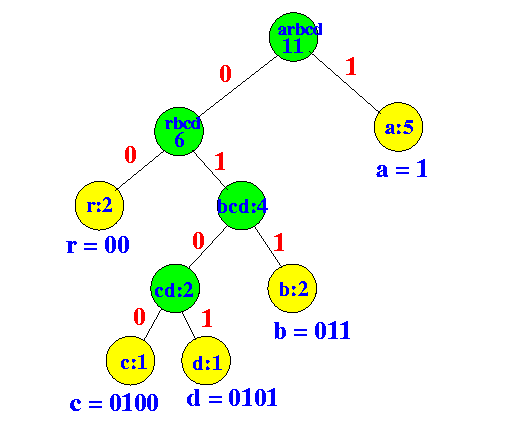
- Huffman code for
abracadabra:
a b r a c a d a b r a 1 011 00 1 0100 1 0101 1 011 00 1 Or: 10110010100101011011001
Notes:
- Verify for yourself that
when you receive the message:
10110010100101011011001
you can decode it by traversing the binary tree built by the algorithm
- The higher the frequency of
a character, the
later that
character is included into the
binary tree
(and will be
located higher up in the tree)
Therefore:
- Characters that are more frequent will be assigned a shorter code
- The binary tree must be included in order to decode the Huffman code !!!
- Find the frequency of each character