Closed Addressing vs. Open Addressing

Closed Addressing:

In closed addressing, each key is always stored in the hash bucket where the key is hashed to.
Closed addressing must use some data structure (e.g.: linked list) to store multiple entries in the same bucket

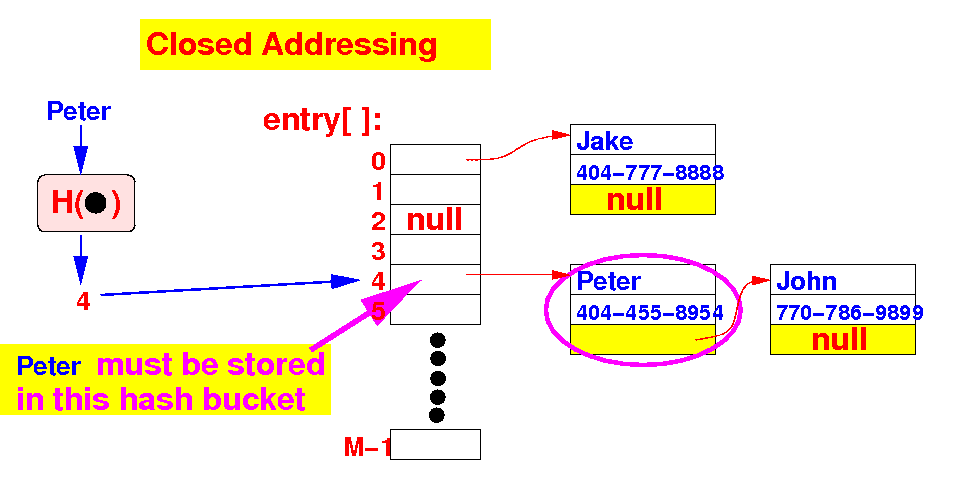
Example of closed addressing: a hash table using separate chaining

Closed Addressing vs. Open Addressing

Open Addressing:

In open addressing, each hash bucket will store at most one hash table entry
In open addressing, a key may be stored in different hash bucket than where the key was hashed to.

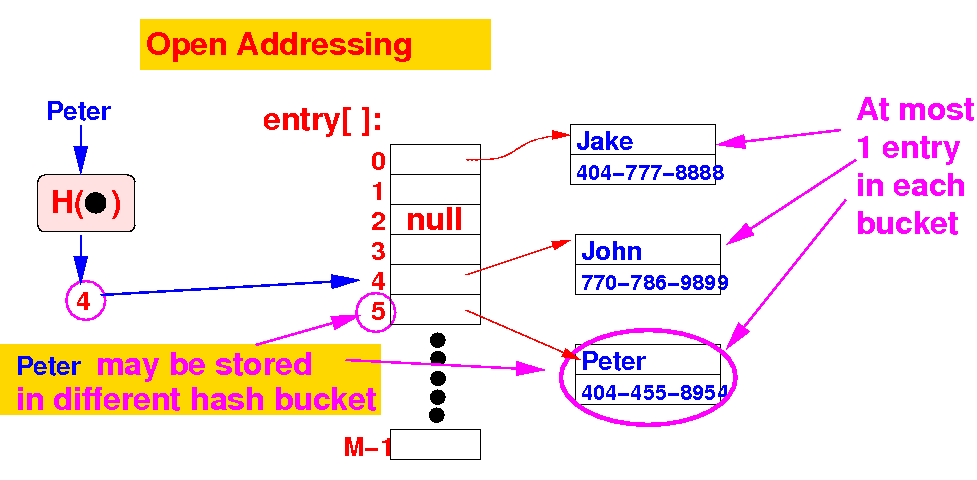
Example of open addressing: Peter hashed into bucket 4 but is stored in bucket 5

Closed Addressing vs. Open Addressing

Entries used in Open Addressing:

Since in open addressing, each hash bucket will store at most one hash table entry:
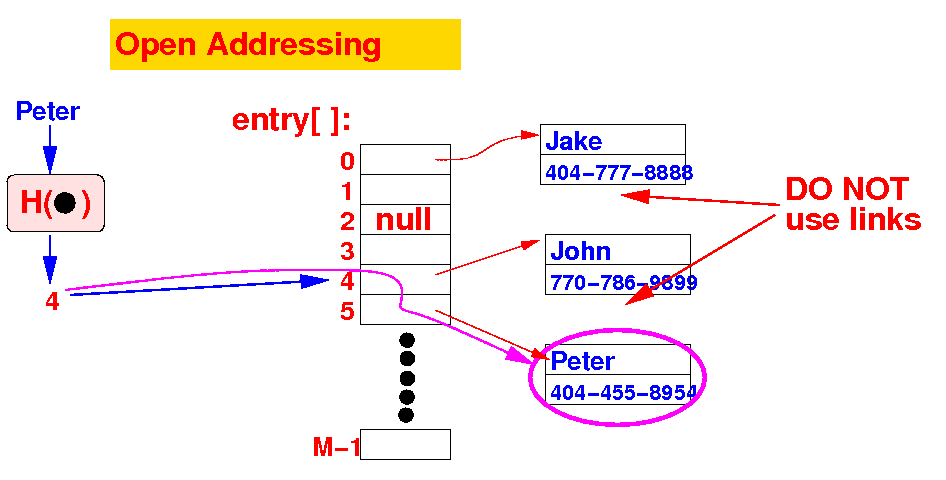
The entries stored In Open Addressing do not has a link variable

Entries used in open addressing: no linking field

The Entry class for a hash table using Open Addressing

We can used the original Entry<K,V> class (which was used in the ArrayMap<K,V>) in the Open Addressing technique:

public class Entry<K,V> { private K key; // Key private V value; // Value public Entry(K k, V v) // Constructor { key = k; value = v; } ... // Methods omitted for brevity }

We have used this Entry<sK,V> class to implement the ArrayMap dictionary data structure
The same Entry object can be used in Open Addressing

Collision resolution in Open Addressing

Suppose 2 different keys (John and Peter) hash into the same hash bucket (e.g.: 4)
The first key (e.g.: John) is inserted in the hash bucket (4):

Now the hash bucket 4 is full
(Because each hash bucket can store at most one hash table entry)

Collision resolution in Open Addressing

Insertion of the second key (e.g.: Peter) will find that the hash bucket (4) is full:

The insert algorithm will start at the hash index and find the next available hash bucket that can use used to store the key
The procedure to find the next available hash bucket is called:
Rehashing
Note: rehashing is not random but deterministic (= computable)

Collision resolution in Open Addressing

Rehash algorithms used to resolve collision in Open Addressing:

Linear Probing:
In linear probing, the hash table is searched sequentially starting from the hash index value
In other words, the "rehash" function is:
rehash(key) = (h+i)%M where h = H(key) and i = 1, 2, ..

Quadratic Probing: uses the "rehash" function:

rehash(key) = (h+i²)%M where h = H(key) and i = 1, 2, ..

Double hashing: which uses the "rehash" function:

rehash(key) = (h+i*H₂(key))%M // H₂ is a 2nd hash function

Linear Probing

We will now study a hash table using Open Addressing with linear probing as collision resolution method
For simplicity:
I will use a hash table with 12 entries

The keys used in the example consists of a single character

The initial (empty} hash table:

0 1 2 3 4 5 6 7 8 9 10 11 +---+---+---+---+---+---+---+---+---+---+---+---+ bucket[] = | | | | | | | | | | | | | +---+---+---+---+---+---+---+---+---+---+---+---+

Remember that in Open Addressing:
Each bucket can store at most one entry (= (key, value) pair)

The insert algorithm in Open Addressing with linear probing

Psuedo code of the insert algorithm using Linear Probing:

void put(Key k, Value v) { int hashValue = H(key); // Hash value Starting at i = hashValue Increasing i = i + 1 // = Linear Probing Algorithm Check every bucket[i]: { if ( bucket[i] == empty ) { bucket[i] = new Entry(k,v); // Insert (k,v) return; } else if ( bucket[i].key == k ) { bucket[i].value = v; // Update value return; } } System.out.println("Full"); }

The insert algorithm in Open Addressing with linear probing

The initial version of the insert algorithm using Linear Probing:

public void put(K k, V v) { int hashIdx = H(k); // Find the hash index for key k int i = hashIdx; do { if ( entry[i] == null ) // Is entry empty ? { bucket[i] = new Entry<>(k,v); return; } else if (entry[i].key == k ) // Does entry contains key k ? { bucket[i].value = v; return; } i = (i + 1)%M; // Check in next hash table entry } while ( i != hashIdx ) // Hash table is full... System.out.println("Full"); }

Note: we need to modify put( ) slightly later (next webpage)

The insert algorithm in Open Addressing with linear probing

Start the search for key k at bucket hashIdx:

public void put(K k, V v) { int hashIdx = H(k); // Find the hash index for key k int i = hashIdx; do { if ( entry[i] == null ) // Is entry empty ? { bucket[i] = new Entry<>(k,v); return; } else if (entry[i].key == k ) // Does entry contains key k ? { bucket[i].value = v; return; } i = (i + 1)%M; // Check in next hash table entry } while ( i != hashIdx ) // Hash table is full... System.out.println("Full"); }

The insert algorithm in Open Addressing with linear probing

Search all the buckets i, i+1, i+2, ...:

public void put(K k, V v) { int hashIdx = H(k); // Find the hash index for key k int i = hashIdx; do { if ( entry[i] == null ) // Is entry empty ? { bucket[i] = new Entry<>(k,v); return; } else if (entry[i].key == k ) // Does entry contains key k ? { bucket[i].value = v; return; } i = (i + 1)%M; // Check in next hash table entry } while ( i != hashIdx ) // All entries searched ! System.out.println("Full"); }

Note: when i == hashIdx again, the search index i has wrap back to the start !

The insert algorithm in Open Addressing with linear probing

If we find an empty entry, then insert (k,v) in that empty entry:

public void put(K k, V v) { int hashIdx = H(k); // Find the hash index for key k int i = hashIdx; do { if ( entry[i] == null ) // Is entry empty ? { bucket[i] = new Entry<>(k,v); return; } else if (entry[i].key == k ) // Does entry contains key k ? { bucket[i].value = v; return; } i = (i + 1)%M; // Check in next hash table entry } while ( i != hashIdx ) // All entries searched ! System.out.println("Full"); }

The insert algorithm in Open Addressing with linear probing

If we find the key k, then update the value with v:

public void put(K k, V v) { int hashIdx = H(k); // Find the hash index for key k int i = hashIdx; do { if ( entry[i] == null ) // Is entry empty ? { bucket[i] = new Entry<>(k,v); return; } else if (entry[i].key == k ) // Does entry contains key k ? { bucket[i].value = v; return; } i = (i + 1)%M; // Check in next hash table entry } while ( i != hashIdx ) // All entries searched ! System.out.println("Full"); }

The insert algorithm in Open Addressing with linear probing

If the hash table is full, we exit without inserting (k,v):

public void put(K k, V v) { int hashIdx = H(k); // Find the hash index for key k int i = hashIdx; do { if ( entry[i] == null ) // Is entry empty ? { bucket[i] = new Entry<>(k,v); return; } else if (entry[i].key == k ) // Does entry contains key k ? { bucket[i].value = v; return; } i = (i + 1)%M; // Check in next hash table entry } while ( i != hashIdx ) // All entries searched ! System.out.println("Full"); }