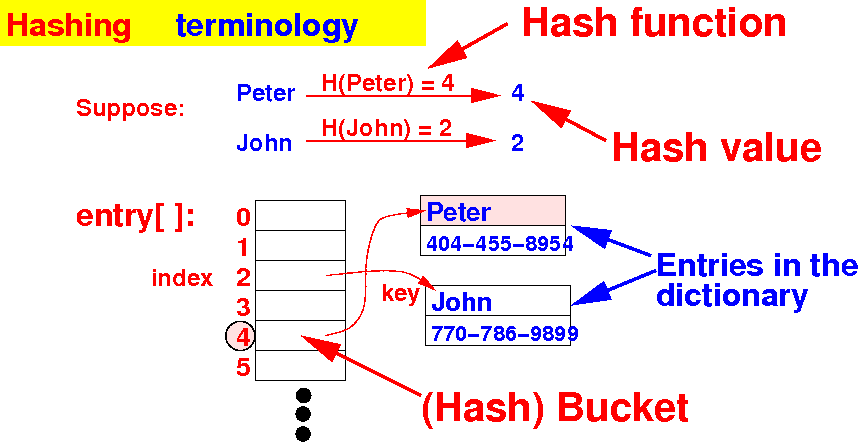
Terminology

  • Hash function H( ):   maps a key k to an integer in the range [0..(M-1)] 

        H(k) = integer in the range [0..(M-1)]

  • Hash value h = the value returned by the hash function H( ) 

        h = H(k)

  • Bucket = the array element used to store an entry of the dictionary

Collision

  • Collision:

    • A collision occurs when:

      • 2 different keys k1 and k2 have the same hash value: 

           k1 ≠ k2   and   H(k1) = H(k2)

    Collision explained with a diagram:

Likelihood (probability) of a collision...

  • Question:

    • If there are n people in a room, how likely is it that 2 people share the same birthday ?

    Answer: let's find the probability that everyone has a different birthday 

     Let a be an arbitrary people in the n people

Likelihood (probability) of a collision...

  • Question:

    • If there are n people in a room, how likely is it that 2 people share the same birthday ?

    Answer: let's find the probability that everyone has a different birthday 

     Let a be an arbitrary people in the n people

 Let b be an arbitrary people in the remaining n-1 people

 Prob[ a and b have different BD ] = 1 - 1/365

Likelihood (probability) of a collision...

  • Question:

    • If there are n people in a room, how likely is it that 2 people share the same birthday ?

    Answer: let's find the probability that everyone has a different birthday 

     Let a be an arbitrary people in the n people

 Let b be an arbitrary people in the remaining n-1 people

 Prob[ a and b have different BD ] = 1 - 1/365

 Let c be an arbitrary people in the remaining n-2 people

 Prob[ a, b, c have different BD ] = (1 - 1/365)x(1 - 2/365)

 And so on...

Likelihood (probability) of a collision...

  • Question:

    • If there are n people in a room, how likely is it that 2 people share the same birthday ?

    Answer: let's find the probability that everyone has a different birthday 

     Let a be an arbitrary people in the n people

 Let b be an arbitrary people in the remaining n-1 people

 Prob[ a and b have different BD ] = 1 - 1/365    

 Let c be an arbitrary people in the remaining n-2 people

 Prob[ a, b, c have different BD ] = (1 - 1/365)x(1 - 2/365)

 Prob[ n people have different BD ] = 

          1x(1 - 1/365)x(1 - 2/365)x .... x (1-(n-1)/365)

          365 x 364 x ... x (365-n+1)         365!
   =     -----------------------------  = --------------
          365 x 365 x ... x 365            365n x (365-n)!

Likelihood (probability) of a collision...

  • Question:

    • If there are n people in a room, how likely is it that 2 people share the same birthday ?

    Answer: 

     Prob[ all n people have different BD ] = 

          365 x 364 x ... x (365-n+1)         365!
   =     -----------------------------  = --------------
          365 x 365 x ... x 365            365n x (365-n)!

 Therefore:

 Prob[ 2 people has the same birthday ] =

                 365!
   =   1 -   --------------
             365n x (365-n)!

 How likely is this ???

    We plot the probabilty for different number of people n...

Likelihood (probability) of a collision...

  • Question:

    • If there are n people in a room, how likely is it that 2 people share the same birthday ?

    Probability that 2 people has the same birthday when there are n people:

    Chance is 50/50 when there are 23 people !!!

Likelihood (probability) of a collision in hashing with hash table size M

  • Question:

    • If there are n entries in a hash table of size M, how likely is it that 2 entries hash into the same bucket ?

    Answer: 

     Prob[ all n entries use different buckets ] = 

          M x (M-1) x ... x (M-n+1)            M!
   =     -----------------------------  = --------------
          M x   M   x ... x    M            Mn x (M-n)!

 Therefore:

 Prob[ 2 entries use the same bucket ] =

                M!
   =   1 - -------------
            Mn x (M-n)!

Handling collisions in hashing

  • There are 2 techniques to handle collision in hashing:

    • (1) Closed addressing (a.k.a: Seperate chaining)

      • Entries are always stored in their hash bucket
         

      • Each bucket of the hash table is organized as a linked list

      Example:

Handling collisions in hashing

  • There are 2 techniques to handle collision in hashing:

    • (2) Open Addressing

      • Entries can be stored in a different bucket than their hash bucket

      • A rehash algorithm is used to find an empty bucket

      Example: