|
|
|
|
|
// Merge sorts the array elements A[s] ... A[e-1] using helper array H
public static <T extends Comparable<T>> void sort(T[] A, int s, int e, T[] H)
{
if ( e - s <= 1 ) // Array of 0 or 1 element
return; // No need to sort an array of 1 element...
int m = (e+s)/2; // Middle
This is NOT the actual Merge Sort algorithm....
/* ------------------------------------------------
"Easy to understand" merge sort:
(1) sort the first half of the array
(2) sort the 2nd half of the array
(3) merge the 2 sorted portions
------------------------------------------------ */
SelectionSort.sort(A, s, m);
But it is very close to the real algorithm...
SelectionSort.sort(A, m, e);
// Merge both sorted arrays
merge(A, s, m, e, H); // We have discussed merge() already...
}
|
Note: I will present an easy to understand (not recursive) version of the Merge sort algorithm
// Merge sorts the array elements A[s] ... A[e-1] using helper array H
public static <T extends Comparable<T>> void sort(T[] A, int s, int e, T[] H)
{
if ( e - s <= 1 ) // A[s]..A[e] has 0 or 1 element
return; // No need to sort an array of 1 element...
int m = (e+s)/2; // Middle
/* ------------------------------------------------
"Easy to understand" merge sort:
(1) sort the first half of the array
(2) sort the 2nd half of the array
(3) merge the 2 sorted portions
------------------------------------------------ */
SelectionSort.sort(A, s, m);
SelectionSort.sort(A, m, e);
// Merge both sorted arrays
merge(A, s, m, e, H); // We have discussed merge() already...
}
|
Check for the base case: if the portion that needs to be sorted has 1 element or less, we are done
// Merge sorts the array elements A[s] ... A[e-1] using helper array H
public static <T extends Comparable<T>> void sort(T[] A, int s, int e, T[] H)
{
if ( e - s <= 1 ) // A[s]..A[e] has 0 or 1 element
return; // No need to sort an array of 1 element...
int m = (e+s)/2; // m = middle of s and e
/* ------------------------------------------------
"Easy to understand" merge sort:
(1) sort the first half of the array
(2) sort the 2nd half of the array
(3) merge the 2 sorted portions
------------------------------------------------ */
SelectionSort.sort(A, s, m);
SelectionSort.sort(A, m, e);
// Merge both sorted arrays
merge(A, s, m, e, H); // We have discussed merge() already...
}
|
Find the middle element: m is the index of the array element that is the middle of A[s] and A[e-1]
// Merge sorts the array elements A[s] ... A[e-1] using helper array H
public static <T extends Comparable<T>> void sort(T[] A, int s, int e, T[] H)
{
if ( e - s <= 1 ) // A[s]..A[e] has 0 or 1 element
return; // No need to sort an array of 1 element...
int m = (e+s)/2; // m = middle of s and e
/* ------------------------------------------------
"Easy to understand" merge sort:
(1) sort the first half of the array
(2) sort the 2nd half of the array
(3) merge the 2 sorted portions
------------------------------------------------ */
SelectionSort.sort(A, s, m);
SelectionSort.sort(A, m, e);
// Merge both sorted arrays
merge(A, s, m, e, H); // We have discussed merge() already...
}
|
Sort the first half: in this simplified (easy to understand) version, we use the SelectionSort( ) to sort
// Merge sorts the array elements A[s] ... A[e-1] using helper array H
public static <T extends Comparable<T>> void sort(T[] A, int s, int e, T[] H)
{
if ( e - s <= 1 ) // A[s]..A[e] has 0 or 1 element
return; // No need to sort an array of 1 element...
int m = (e+s)/2; // m = middle of s and e
/* ------------------------------------------------
"Easy to understand" merge sort:
(1) sort the first half of the array
(2) sort the 2nd half of the array
(3) merge the 2 sorted portions
------------------------------------------------ */
SelectionSort.sort(A, s, m);
SelectionSort.sort(A, m, e);
// Merge both sorted arrays
merge(A, s, m, e, H); // We have discussed merge() already...
}
|
Sort the 2nd half: we will again use the SelectionSort( ) to sort
// Merge sorts the array elements A[s] ... A[e-1] using helper array H
public static <T extends Comparable<T>> void sort(T[] A, int s, int e, T[] H)
{
if ( e - s <= 1 ) // A[s]..A[e] has 0 or 1 element
return; // No need to sort an array of 1 element...
int m = (e+s)/2; // m = middle of s and e
/* ------------------------------------------------
"Easy to understand" merge sort:
(1) sort the first half of the array
(2) sort the 2nd half of the array
(3) merge the 2 sorted portions
------------------------------------------------ */
SelectionSort.sort(A, s, m);
SelectionSort.sort(A, m, e);
// Merge both sorted arrays
merge(A, s, m, e, H); // We have discussed merge() previously !
}
|
Merge the 2 sorted protions: we use the merge( ) algorithm discussed in the last set of slides
public static void main(String[] args)
{
Integer[] list = {4, 3, 2, 7, 1, 5, 8, 6};
Integer[] H = new Integer[list.length];
for(int i = 0; i < list.length; i++)
System.out.print(list[i] + " ");
System.out.println();
MergeSort.sort(list, 0, list.length, H);;
for (int i = 0; i < list.length; i++)
System.out.print(list[i] + " ");
System.out.println();
}
|
DEMO: demo/14-sort/11-merge-sort/Demo.java + MergeSort.java + SelectionSort.java
The easy to understand Merge Sort algorithm uses the Selection sort algorithm to sort the array portions:
// Merge sorts the array elements A[s] ... A[e-1] using helper array H
public static <T extends Comparable<T>> void sort(T[] A, int s, int e, T[] H)
{
if ( e - s <= 1 ) // A[s]..A[e] has 0 or 1 element
return; // No need to sort an array of 1 element...
int m = (e+s)/2; // m = middle of s and e
/* ------------------------------------------------
"Easy to understand" merge sort:
(1) sort the first half of the array
(2) sort the 2nd half of the array
(3) merge the 2 sorted portions
------------------------------------------------ */
SelectionSort.sort(A, s, m);
SelectionSort.sort(A, m, e);
// Merge both sorted arrays
merge(A, s, m, e, H); // We have discussed merge() previously !
}
|
Because the Merge Sort algorithm can sort an array, we can use the merge sort algorithm instead !!!
The real Merge Sort algorithm is a recursive (= divide and conquer) sorting algorithm:
// Merge sorts the array elements A[s] ... A[e-1] using helper array H
public static <T extends Comparable<T>> void sort(T[] A, int s, int e, T[] H)
{
if ( e - s <= 1 ) // A[s]..A[e] has 0 or 1 element
return; // No need to sort an array of 1 element...
int m = (e+s)/2; // m = middle of s and e
/* ------------------------------------------------
The actual merge sort:
(1) sort the first half of the array using MergeSort
(2) sort the 2nd half of the array using MergeSort
(3) merge the 2 sorted portions
------------------------------------------------ */
MergeSort.sort(A, s, m, H);
MergeSort.sort(A, m, e, H);
// Merge both sorted arrays
merge(A, s, m, e, H); // We have discussed merge() previously !
}
|
I will illustrate the recursive Merge Sort algorithm with diagrams next...
Consider the mergeSort( ) algorithm on the following input: the parameters are s=0 and e=8

mergeSort(0,8) |
mergeSort(0,8) first split the input array into 2 halves: m = (8+0)/2 = 4
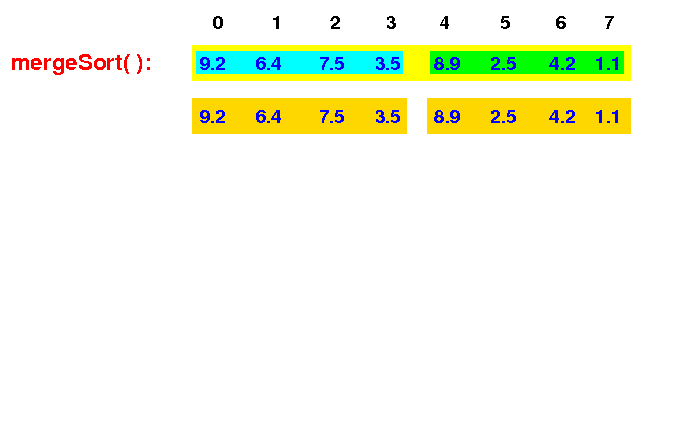
mergeSort(0,8) |
mergeSort(0,8) then recurses and call mergeSort(0,4) to sort the left half of the input array:
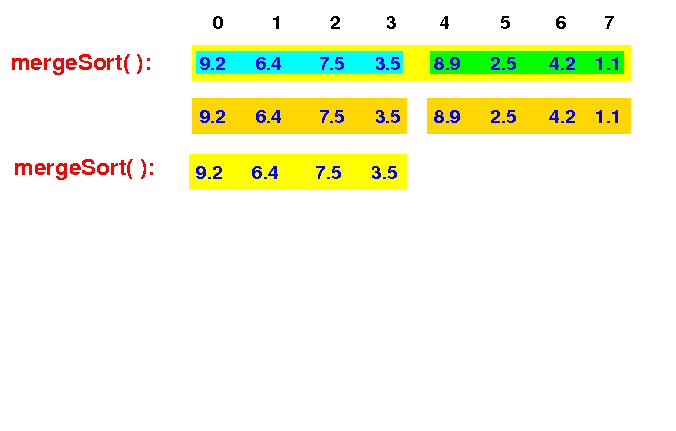
mergeSort(0,8) -> mergeSort(0,4) |
The new mergeSort(0,4) first split the input array into 2 halves: m = (4+0)/2 = 2
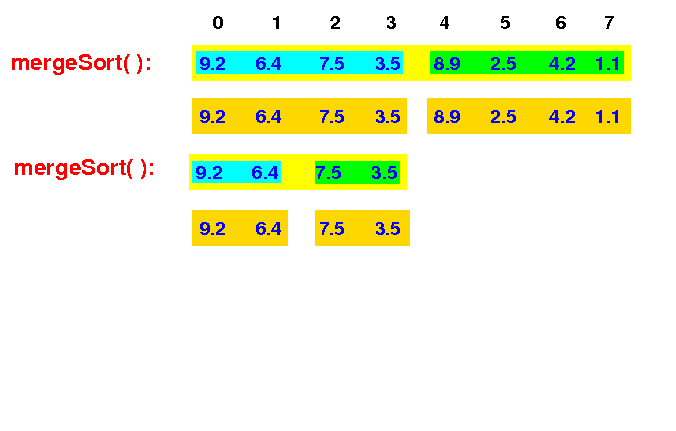
mergeSort(0,8) -> mergeSort(0,4) |
This mergeSort(0,4) then recurses can call mergeSort(0,2) and sort the left half of the array:
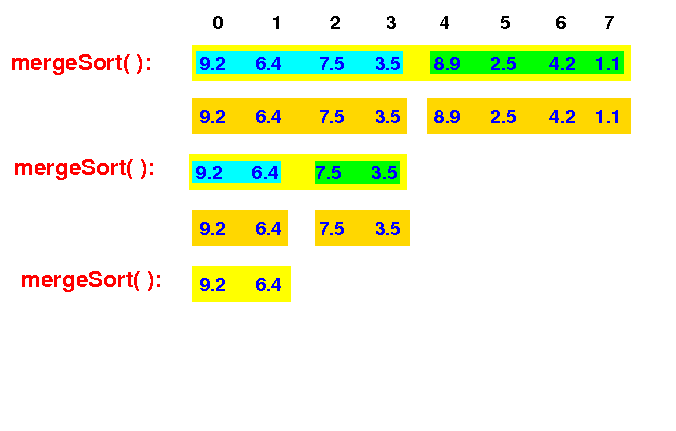
mergeSort(0,8) -> mergeSort(0,4) -> mergeSort(0,2) |
The new mergeSort(0,2) first split the input array into 2 halves: m = (2+0)/2 = 1
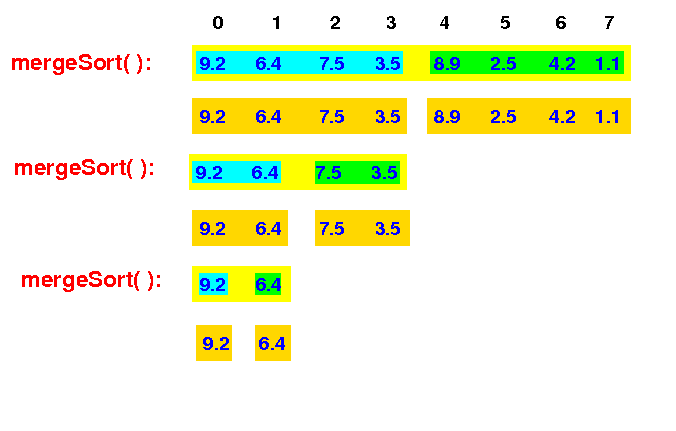
mergeSort(0,8) -> mergeSort(0,4) -> mergeSort(0,2) |
This mergeSort(0,2) then recurses and call mergeSort(0,1) sort the left half of the array:
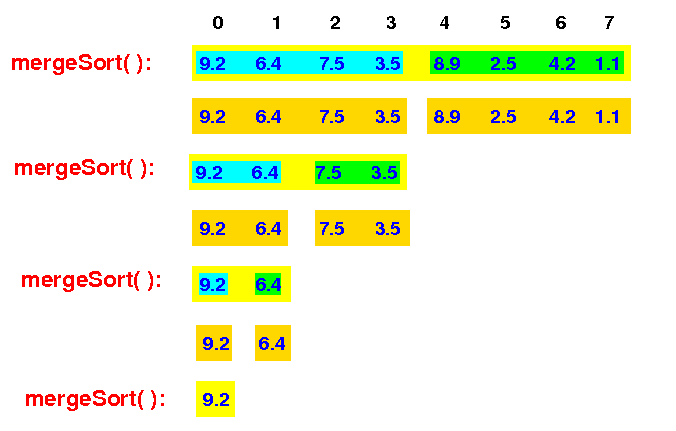
mergeSort(0,8) -> mergeSort(0,4) -> mergeSort(0,2) -> mergeSort(0,1) |
The input array consists of 1 element (= base case) and mergeSort(0,1) returns to mergeSort(0,2)
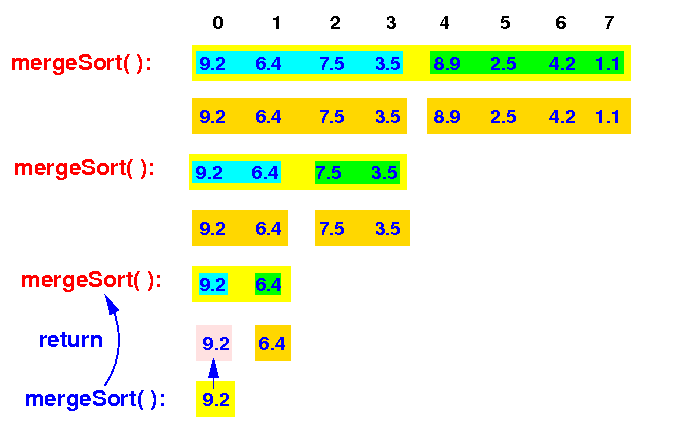
mergeSort(0,8) -> mergeSort(0,4) -> mergeSort(0,2) <- |
The mergeSort(0,2) then recurses and call mergeSort(1,2) to sort the right half of the array:
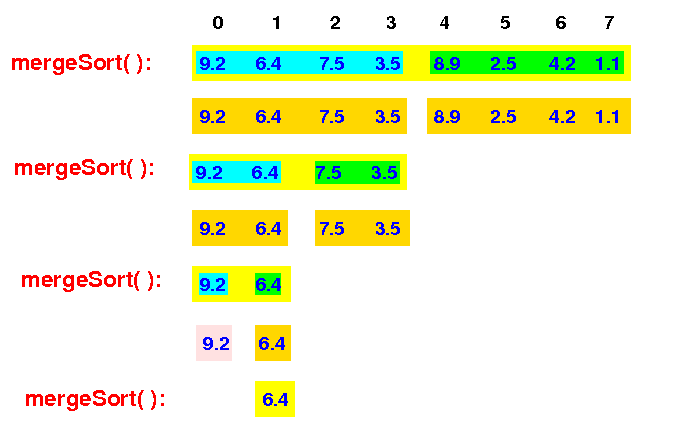
mergeSort(0,8) -> mergeSort(0,4) -> mergeSort(0,2) -> mergeSort(1,2)
|
The input array consists of 1 element (= base case) and mergeSort(1,2) returns
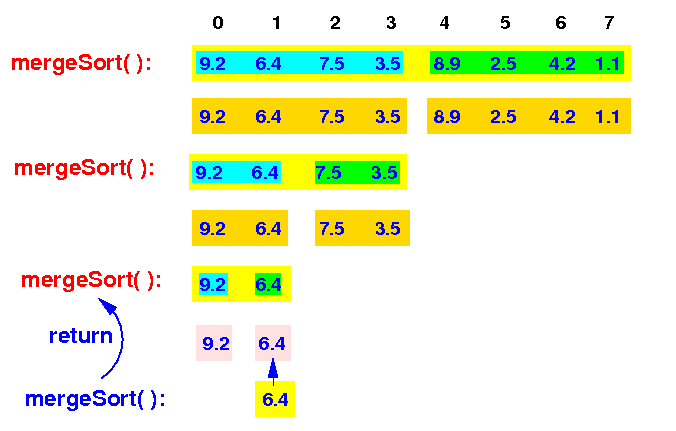
mergeSort(0,8) -> mergeSort(0,4) -> mergeSort(0,2) <-- both halves sorted |
mergeSort(0,2) will finally merge the 2 sorted arrays and return to the caller mergeSort(0.4):
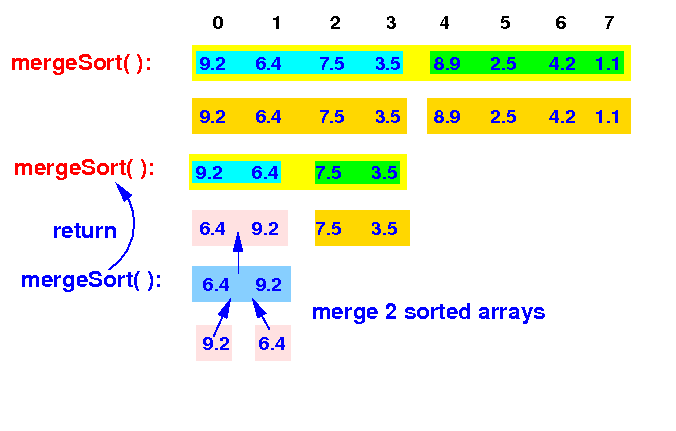
mergeSort(0,8) -> mergeSort(0,4) <--- left portion is sorted |
This mergeSort(0,4) then recurses and call mergeSort(2,4) to sort the right half of the array:
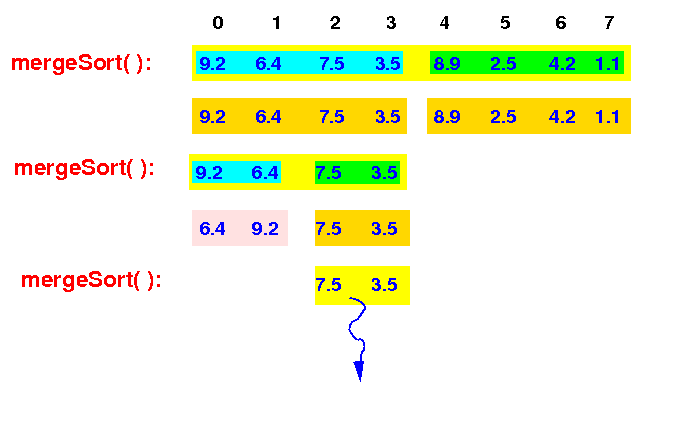
mergeSort(0,8) -> mergeSort(0,4) -> mergeSort(2,4) (and so on)
|
MergeSort(2,4) will repeat the previously shown steps (omitted) - the end result is it sorts the input array:

The same steps are repeated for the right array.. |
The 2nd level mergeSort(0,4) will merge the 2 sorted arrays and ...
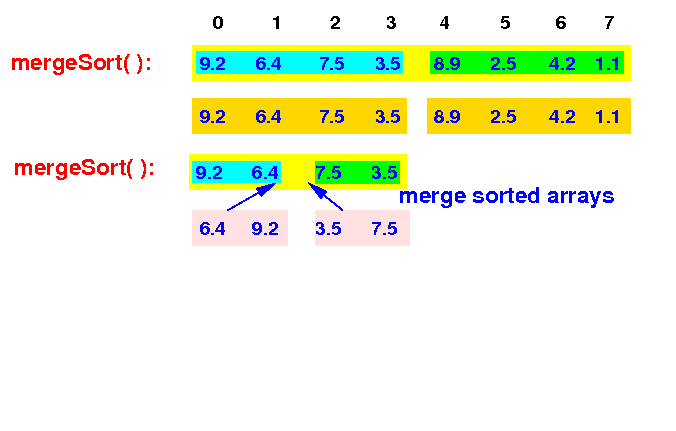
left and right halves are sorted and then merged... |
The 2nd level mergeSort(0,4) will merge the 2 sorted arrays and return to the top level mergeSort(0,8):

The 2nd level Merge Sort will return to the top level Merge sort... |
The top level mergeSort(0,8) then recurses and call mergeSort(4,8) to sort the right half of the array:
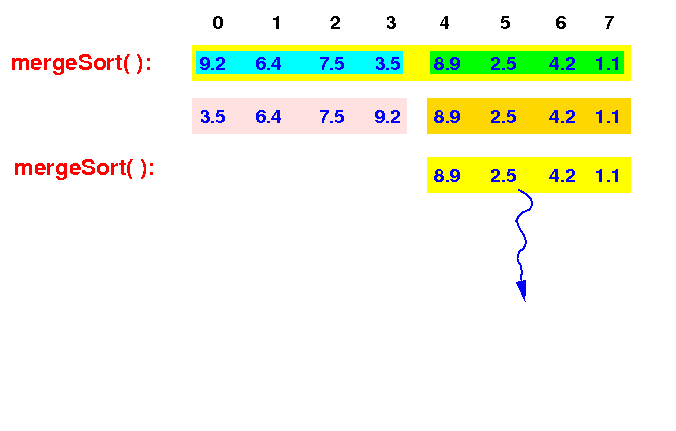
The top level Merge Sort will repeat the steps for the right half of the array... |
mergeSort(4,8) will repeat the previously shown steps (omitted) - the end result is it sorts the right array:

The result is: the right half of the array is sorted... |
Finally, the top level mergeSort(0,8) will have 2 sorted arrays:
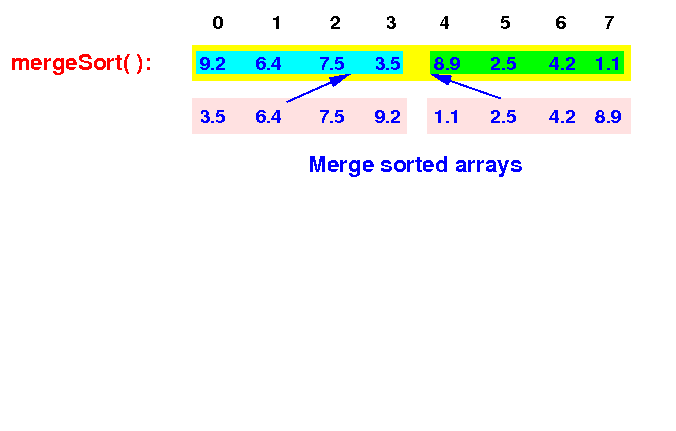
The final result: the entire array is sorted ! |
The top level mergeSort(0,8) merges the 2 sorted array and obtains the final result:
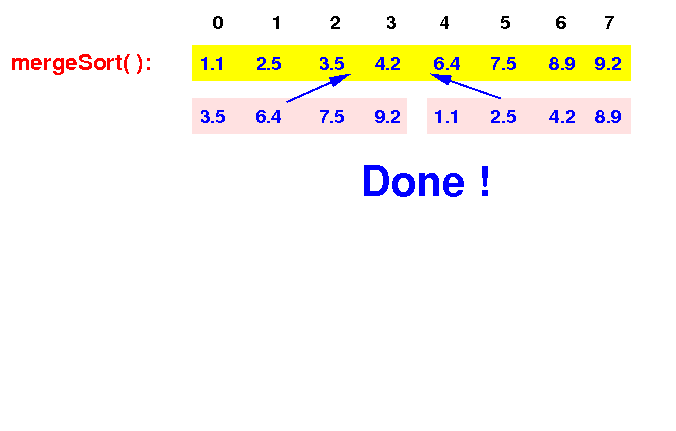
Next: Demo merge sort
|
public static void main(String[] args)
{
Integer[] list = {6, 3, 8, 2, 5, 1, 7, 4};
Integer[] H = new Integer[list.length]; // Helper array for Merge
System.out.println("\nInput:");
for (int i = 0; i < list.length; i++)
System.out.print(list[i] + " ");
System.out.println("\n");
MergeSort.sort(list, 0, list.length, H);
System.out.println("\nResult:");
for (int i = 0; i < list.length; i++)
System.out.print(list[i] + " ");
System.out.println();
}
|
DEMO: demo/14-sort/12-merge-sort/Demo.java + MergeSort.java
|