- Definite integral (High School material):
- A definite integral
a∫b f(x) dx
is
the integral of
a function f(x)
with
fixed end point a and b:
- The integral of
a function f(x)
is equal to the
area under
the graph of f(x).
- Graphically explained:
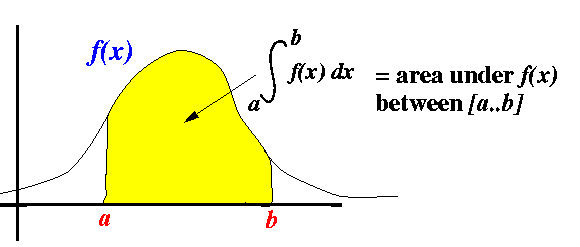
- A definite integral
a∫b f(x) dx
is
the integral of
a function f(x)
with
fixed end point a and b:
- Rectangle Method:
- The rectangle method
(also called the midpoint rule)
is the
simplest method
in Mathematics used to
compute an approximation
of a
definite integral.
- The rectangle method
(also called the midpoint rule)
is the
simplest method
in Mathematics used to
compute an approximation
of a
definite integral.
- Rectangle Method:
- Divide the
interval [a .. b]
into n pieces;
each piece has the same width:
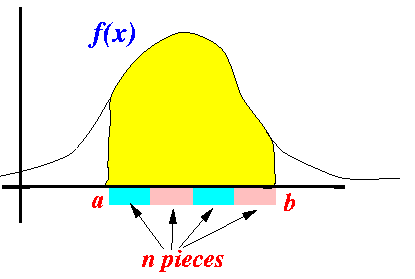
The width of each piece of the smaller intervals is equal to:
b - a width = ------- n
- The definite integral
(= area under the graph
is approximated using
a series of rectangles:
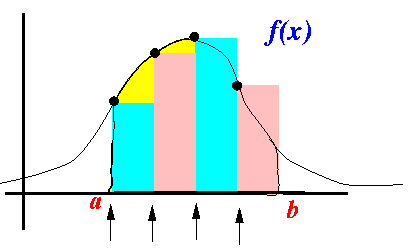
The area of a rectangle is equal to:
area of a rectangle = width × height
We (already) know the width of each rectangle:
b - a width = ------- nWe still need to find the height of each rectangle.
- Divide the
interval [a .. b]
into n pieces;
each piece has the same width:
- The height of the
rectangles:
- The different rectangles
has different heights
- Heights of each rectange:
- The heights of each rectangle = the function value at the start of the (small) interval
- Example: first interval
- First (small) interval:
[a .. (a + width)]
(remember that:
width = (b − a)/n)
- Height of
first (small) interval:
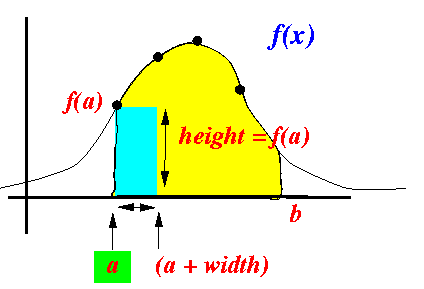
Therefore: height of first rectangle = f(a)
- Area of the rectangle = f(a) × width
- First (small) interval:
[a .. (a + width)]
(remember that:
width = (b − a)/n)
- Example: second interval
- the second (small) interval is
[(a+width) .. (a+2width)]
(remember that:
width = (b − a)/n)
- Height of
first (small) interval:
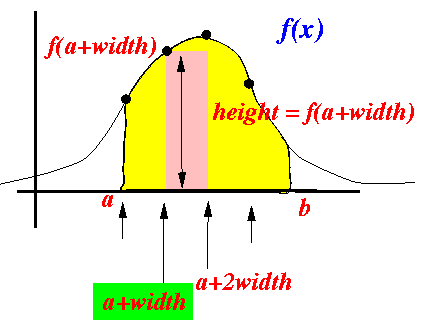
Therefore: height of first rectangle = f(a+width)
- Area of the rectangle = f(a+width) × width
- the second (small) interval is
[(a+width) .. (a+2width)]
(remember that:
width = (b − a)/n)
- Example: third interval
- the third (small) interval is
[(a+2width) .. (a+3width)]
(remember that:
width = (b − a)/n)
- Height of
first (small) interval:
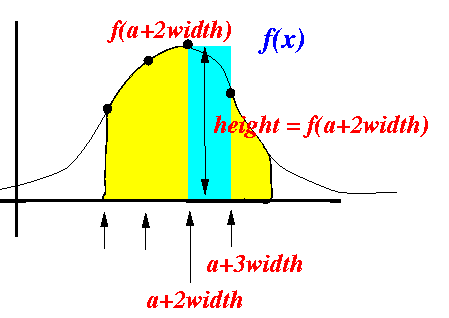
Therefore: height of first rectangle = f(a+2width)
- Area of the rectangle = f(a+2width) × width
- the third (small) interval is
[(a+2width) .. (a+3width)]
(remember that:
width = (b − a)/n)
- We see a pattern
emerging:
- Height of rectangle 1 = f(a + 0×width)
- Height of rectangle 2 = f(a + 1×width)
- Height of rectangle 3 = f(a + 2×width)
- ...
- Height of rectangle n−1 = f(a + (n−2)×width)
- Height of rectangle n = f(a + (n−1)×width)
Note: there are n (smaller) interval in total.
Conclusion:
Height of rectangle i = f( a + (i-1)*width ) = the function value at the point "a + (i-1)*width" b-a Recall that: width = ----- n
- The different rectangles
has different heights
- The area of the
rectangles:
- This figure helps you to visualize the compuation:
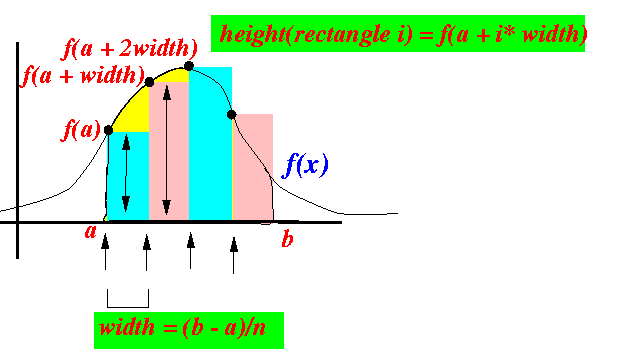
- The width of
rectangle i is equal to:
b - a width = ------- n
- The height of
rectangle i is equal to:
height = f( a + (i-1)×width )
- The area of
rectangle i is equal to:
area = width × height = width × f( a + (i-1)×width )
- This figure helps you to visualize the compuation:
- The approximation of the
definite integral:
Aproximation = sum of the area of the rectangles = area of rectangle 1 + area of rectangle 2 + ... + area of rectangle n = width × f( a + (1-1)×width ) + width × f( a + (2-1)×width ) + ... + width × f( a + (n-1)×width )
- We have seen a
running sum
computation algorithm previously that adds
in simple series of numbers:
- Compute the sum:
1 + 2 + 3 + .... + n
- Running sum algorithm:
sum = 0; // Clear sum for ( i = 1; i <= n ; i++ ) { sum = sum + i; // Add i to sum }
- Compute the sum:
1 + 2 + 3 + .... + n
- The running sum algorithm can be
generalized to add
a more general series
Example: compute 12 + 22 + 32 + ... + i2 + ... + n2
- The ith term
in the sum =
i2
- Therefore, the running sum algorithm
to compute this sum is:
sum = 0; // Clear sum for ( i = 1; i <= n ; i++ ) { sum = sum + i*i; // Add i2 to sum }
- The ith term
in the sum =
i2
- We can use the running sum algorithm
to compute the
sum of the area of the rectangles
- Recall:
Aproximation = sum of the area of the rectangles = width × f( a + (1-1)×width ) + width × f( a + (2-1)×width ) + ... + width × f( a + (i-1)×width ) + ... + width × f( a + (n-1)×width ) Where: width = (b - a) / n
- The ith term of
the running sum is
equal to:
ith term = width × f( a + (i-1)×width )
- Algorithm to compute
the sum of the
area of the rectangles:
Variables: double w; // w contains the width double sum; // sum contains the running sum Algorithm to compute the sum: w = (b - a)/n; // Compute width sum = 0.0; // Clear running sum for ( i = 1; i <= n; i++ ) { sum = sum + w*f( a + (i-1)*w ); }
- Rough algorithm (pseudo code):
input a, b, n; // a = left end point of integral // b = right end point of integral // n = # rectangles used in the approximation
Rectangle Method: w = (b - a)/n; // Compute width sum = sum of area of the n rectangles; // Compute area print sum; // Print result
- Algorithm in Java:
public class RectangleMethod01 { public static void main(String[] args) { double a, b, w, sum, x_i; int i, n; **** Initialize a, b, n **** /* --------------------------------------------------- The Rectangle Rule Algorithm --------------------------------------------------- */ w = (b-a)/n; // Compute width sum = 0.0; // Clear running sum for ( i = 1; i <= n; i++ ) { x_i = a + (i-1)*w; // Use x_i to simplify formula... sum = sum + ( w * f(x_i) ); // width * height of rectangle i } System.out.println("Approximate integral value = " + sum); } }
- Example 1:
compute
0∫1 x3 dx
(the exact answer = 0.25)
public class RectangleMethod01 { public static void main(String[] args) { double a, b, w, sum, x_i; int i, n; a = 0.0; b = 1.0; // 1∫2x3 dx n = 1000; // Use larger value for better approximation /* --------------------------------------------------- The Rectangle Rule Algorithm --------------------------------------------------- */ w = (b-a)/n; // Compute width sum = 0.0; // Clear running sum for ( i = 1; i <= n; i++ ) { x_i = a + (i-1)*w; sum = sum + ( w * (x_i * x_i * x_i) ); // f(x_i) = (x_i)3 } System.out.println("Approximate integral value = " + sum); } }
- Example Program:
(Demo above code)

- Prog file: click here
How to run the program:
- Right click on link and
save in a scratch directory
- To compile: javac RectangleMethod01.java
- To run:
java RectangleMethod01
Output: Approximate integral value = 0.2495002499999998
Exact answer: 0.25
- Example:
compute
1∫2 (1/x) dx
(the answer = ln(2))
public class RectangleMethod02 { public static void main(String[] args) { double a, b, w, sum, x_i; int i, n; a = 1.0; b = 2.0; // 1∫2(1/x) dx n = 1000; // Use larger value for better approximation /* --------------------------------------------------- The Rectangle Rule Algorithm --------------------------------------------------- */ w = (b-a)/n; // Compute width sum = 0.0; // Clear running sum for ( i = 1; i <= n; i++ ) { x_i = a + (i-1)*w; sum = sum + ( w * (1/x_i) ); // f(x_i) = 1/x_i } System.out.println("Approximate integral value = " + sum); } }
- Example Program:
(Demo above code)

- Prog file: click here
How to run the program:
- Right click on link and
save in a scratch directory
- To compile: javac RectangleMethod02.java
- To run:
java RectangleMethod02
Output: Approximate integral value = 0.6933972430599376
Exact answer: ln(2) = 0.69314718
- Difference in the
approximations when
using different number of rectangles:
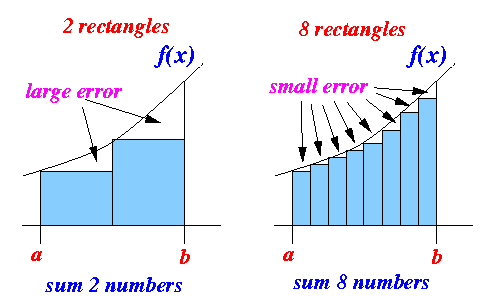
Clearly:
- Using more rectangles will give us a more accurate approximation of the area under the graph
However:
- Using
more rectangles
will make the
algorithm add more
numbers
I.e., the algorithm must do more work --- it must adds more smaller values (because the rectangles are smaller and have smaller areas))
- Trade off:
- Often, in
computer algorithms,
a more accurate result
can be obtained
by a longer running execution
of the
same algorithm
- We call this phenomenon:
trade off
- You cannot gain something without give up on something else
You can experience the trade off phenomenon by using n = 1000000 in the above algorithm.
It will run slower, but give you very accurate results !
Outputs for n = 1000000:
- Approximate integral value of 0∫1 x3 dx = 0.24999950000025453
- Approximate integral value of 1∫2 (1/x) dx = 0.6931474305600139
- Often, in
computer algorithms,
a more accurate result
can be obtained
by a longer running execution
of the
same algorithm